|
| 一、选择题:
1、如图所示,平行四边形ABCD中,已知∠ABC=60°,则∠BAD的度数是( )
A. 60° B. 120° C. 150° D. 无法确定
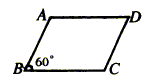
第1题
2、平行四边形具有而一般四边形不具有的性质是( ).
A. 内角和等于360° B. 外角和等于360° C. 不稳定性 D. 对边平行且相等.
3、在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A. 1:2:3:4 B. 2:2:3:3 C. 2:3:2:3 D. 2:3:3:2
4、已知△ABC,若存在点D使以A、B、C、D为顶点的四边形是平行四边形,则这样的点D有( )
A.1个 B.2个 C.3个 D.4个
5、如图,在平行四边形ABCD中,剪去大小不同的平行四边行EGFC,得到另两个图形,将三个图形分别标上(L)、(M)、(N),记周长分别为l、m、n,则必有( )
A.n<m<l B.l<n<m C.l=m=n D.无法确定
(第5题)
6、下面命题中,正确的是( )
A. 一组对角相等的四边形是平行四边形 B. 一组对角互补的四边形是平行四边形
C. 两组边分别相等的四边形是平行四边形 D. 两组对角分别相等的四边形是平行四边形.
7、已知四边形ABCD中,AC交BD于点O,如果只给出条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形。
②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形。
③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形。
④如果再加上条件“∠DBA=∠CAB”,那么平行四边形ABCD一定是平行四边形。
其中正确的说法是( )
A. ①和② B. ①、③和④ C. ②和③ D. ②、③和④
8、平行四边形的一边的长为10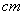 ,则这个平行四边形的两条对角线的长可以是( ). ,则这个平行四边形的两条对角线的长可以是( ).
A.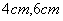 B. B.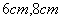 C. C.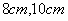 D. D.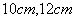
二、填空题:
9、如图,在平行四边形ABCD中,∠A=125°,∠B=________度。
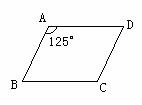
(第9题) | 10、如图10,平行四边形ABCD的周长为16cm,AC,BD相交于点O,OE⊥AC于O,则△DCE的周长为_________
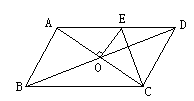
(第10题)
11、根据图中所给的尺寸和比例,可知这个“十”字标志的周长为 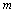 . .

(第11题)
12、把两个全等的不等边三角形拼成平行四边形,可拼成的不同平行四边形的个数为____.
13、平行四边形ABCD中,AC=10cm,BD=8cm,则AB的取值范围是_________。
三、解答题:
14、如图所示,在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF。请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并说明它和图中已有的某一条线段相等(只须说明一组线段相等即可)。
(第14题)
(1)连接____________;
(2)猜想:____________=____________;
(3)说明所猜想的结论的正确性。
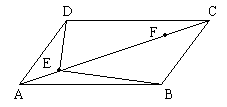
15、平行四边形ABCD中,EF∥AD,GH∥CD,MN∥GH,GH、MN交EF于O、Q,图中共有多少个平行四边形。
第15题
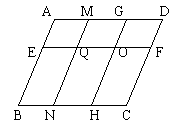
16、李大伯家有一口如图所示的四边形的池塘,在它的四个角上均有一棵大柳树,李大伯开挖池塘,使池塘面积扩大一倍,又想保持柳树不动,如果要求新池塘成平行四边形的形状.请问李大伯愿望能否实现?若能,请画出你的设计;若不能,请说明理由.
(第16题)
17、如图所示,已知四边形ABCD,从(1)AB//DC;(2)AB=DC;(3)AD//BC;(4)AD=BC;(5)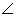 A= A=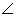 C;(6) C;(6)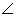 B= B=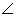 D中取两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种情形?请写出具体组合。 D中取两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种情形?请写出具体组合。

(第17题)
18、梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/s的速度移动,点Q从点C开始沿CB向点B以2cm/s的速度移动,如果P、Q分别从A、C同时出发,设移动时间为t。
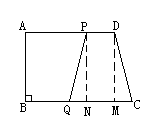
(第18题)
当t为何值时,四边形PDCQ是平行四边形。
平行四边形专项训练参考答案
一、选择题
1.B. 2.D. 3.C. 4. C. 5. C. 6. D. 7.C. 8.D.
二、填空题
9. 55 10. 8cm. 11. 4 12. 3个 13.1 cm <AB<9 cm
三、解答题
14. 解:(1)连接BF;
(2)猜想:BF=DE
解:如图12-1-14所示,连接DB、DF、BF、DB、AC交于点O
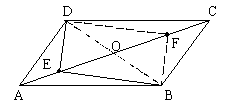
图12-1-14
因为四边形ABCD为平行四边形,则
AO=OC,DO=OB(平行四边形的对角线互相平分)
又AE=FC(已知)
AO-AE=OC-FC
即EO=FO
则四边形EBFD为平行四边形(对角线互相平分的四边形是平行四边形)
所以BF=DE(平行四边形的对边相等)
15.答:平行四边形AMEQ,平行四边形AMNB,平行四边形AGOE,
平行四边形AGHB,平行四边形ADFE,平行四边形ADCB,
平行四边形MGOQ,平行四边形MGHN,平行四边形MDFQ,
平行四边形MDCN,平行四边形GDFO,平行四边形GDCH,
平行四边形EQNB,平行四边形EOHB,平行四边形EFCB,
平行四边形QOHN,平行四边形QFCN,平行四边形OFCH
共18个。
16. 如图所示,连结对角线AC、BD,过A、B、C、D分别作BD、AC、BD、AC的平行线,且这些平行线两两相交于E、F、G、H,四边形EFGH即为符合条件的平行四边形.
17.本题6个条件中任取2个,共有15种组合情形,其中能证明是平行四边形的有9种情况:
①(1),(3) ②(2),(4)
③(5),(6) ④(1),(2)
⑤(3),(4) ⑥(1),(5)
⑦(1),(6) ⑧(3),(5)
⑨(3),(6)
18.解:因为AD∥BC,当DP=CQ时,四边形PDCQ是平行四边形,
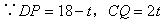
即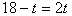
∴t=6
答:当t=6s时,四边形PDCQ是平行四边形。
|