|
一、填空题:(2分×20)
1. 9的平方根是 ; -27的立方根是 ; 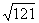 的算术平方根是______.
的算术平方根是______.
2.下列各数中: 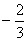 ,
, 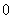 ,
, 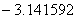 ,
, 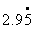 ,
, 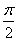 ,
, 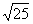 ,
, 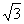 ,是无理数的有 个.
,是无理数的有 个.
3. 直线 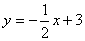 与y轴的交点坐标为______,与x轴的交点坐标为_______.
与y轴的交点坐标为______,与x轴的交点坐标为_______.
4.已知点P(-3,x)与点Q(y, 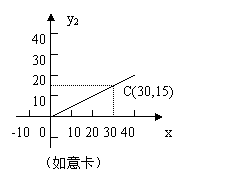 )关于x轴对称,则x=______,y=_______.
)关于x轴对称,则x=______,y=_______.
5.当a取 时 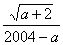 在实数范围内有意义,当a取 时在实数范围内无意义.
在实数范围内有意义,当a取 时在实数范围内无意义.
6.若2<x<5,化简 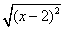 │x-5│=__________.
│x-5│=__________.
7.已知三角形的面积是25cm2,则底边长y(cm)与这条底上的高x(cm) 的函数关系式是_________________.
8. 若函数y=(2m-1)x与y= 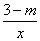 的图象交于一、三象限,则m的取值范围是 . 的图象交于一、三象限,则m的取值范围是 .
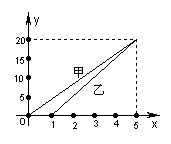
9.左图是一追及图,用y表示路程(千米),用x表示时间(小时),两人同地不同时出发,运动过程中各自的速度不变,则由图象可知: 用了 小时追上 。
 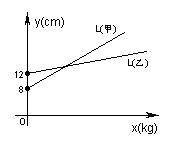
10.如上右图,L甲、L乙分别是甲、乙两弹簧的长y(cm)与所挂物体质量x(kg)之间的函数关系的图象,设甲弹簧每挂1kg物体伸长的长度为k甲cm,乙弹簧每挂1kg物体伸长的长度为k乙cm,则k甲与k乙的大小关系是: k乙 k甲。
11.若点A(7,y1),B(3,y2)在反比例函数y= 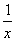 的图象上,则y1与y2的大小关系是_________.
的图象上,则y1与y2的大小关系是_________.
12.直线y=x 1向下平移两个单位得到的直线解析式为_______________,向右平移两个单位得到的直线解析式为__________________.
二、选择题:(2分×10)
1.下列说法正确的个数是( )
①无理数就是开方开不尽的数; ②开方开不尽的数是无理数;
③数轴上的任意一点都表示有理数;④任何一个有理数都可以用数轴上的点来表示.
A.1 B.2 C.3 D.4
2.下列各组二次根式中,是同类二次根式的是( )
A. 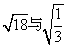 ; B.
; B. 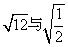 ; C.
; C. 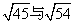 ; D.
; D. 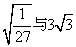
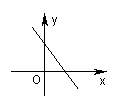 3.若一次函数y=(m-1)x 2m 1的图象如图所示(其中m为常数),则m 的取值范围是( ) 3.若一次函数y=(m-1)x 2m 1的图象如图所示(其中m为常数),则m 的取值范围是( )
A.m>1; B.- 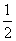 <m<1; C.m<-
<m<1; C.m<- 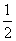 ; D.m>1或m<-
; D.m>1或m<- 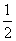
4. 假如函数 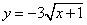 的值大于-3,则自变量x的取值范围是( ). 的值大于-3,则自变量x的取值范围是( ).
A x>0 B x<0 C -1≤x≤0 D -1≤x<0
5.下列各点中,在第三象限的点是 ( )
A.(2,4) B.(-2,4) C. (2,-4) D.(-2,-4)
6.当k<0, x<0时,反比例函数y= 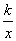 的图象在( )
的图象在( )
A 第二象限 B 第四象限 C 第三象限 D第一象限
7.如图,函数y= 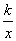 和y=-x-k(
和y=-x-k( 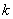 ≠0)在同一坐标系中的大致图象是( ) ≠0)在同一坐标系中的大致图象是( )
   
(A) (B) (C) (D)
8. 一条直线与直线y=2x-3关于x轴对称,则该直线的函数关系式为( )
A 、y= -2x 3 B、y= -2x-3 C、y=2x 3 D、y= -3x 2
9.把(1-a) 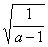 根号外的因式移到根号内,结果是( )
根号外的因式移到根号内,结果是( )
A. 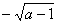 B
B 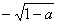 C
C 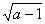 D
D 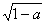
10.已知a-2 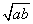 b=0(a>0,b>0),则
b=0(a>0,b>0),则 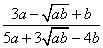 等于 ( )
等于 ( )
A. 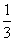 B.
B. 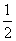 ; C.
; C. 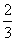 D.
D. 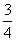
三、计算题:(4分 4分 6分)
1. 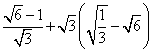 ; 2.
; 2. 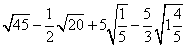 ;
;
3.已知 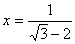 ,
, 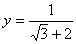 ,求
,求 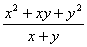 .
.
四、解答题:(4分 6分 8分 8分)
1. ①当 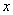 为何值时,
为何值时, 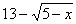 的值最大,最大值是多少?
的值最大,最大值是多少?
②当 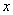 为何值时,
为何值时, 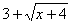 的值最小,最小值是多少?
的值最小,最小值是多少?
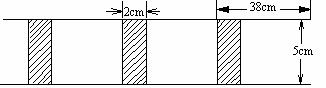
2.将长为38cm,宽为5cm的长方形白纸,按如图所示方法粘合在一起,粘合部分白纸为2cm。
(1)求10张白纸粘合后的长度;
(2)设x张白纸粘合后的总长为ycm,写出y与x的函数关系式。
3.农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售, 他手中持有的钱数(含备用零钱)y(元)与售出的土豆x(千克)的关系如图所示,结合图象回答下列问题:
 (1)农民自带的零钱是 元。 (1)农民自带的零钱是 元。
(2)试求降价前y与x之间的关系式.
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
4.某人从A城出发,前往离A城30千米的B城。现在有三种车供他选择:①自行车,其速度为15千米/时;②三轮车,其速度为10千米/时;③摩托车,其速度为40千米/小时。
(1)用哪些车能使他从A城到达B城的时间不超过2小时,请说明理由。
 (2)设此人在行进途中离B城的路程为s千米,行进时间为小时,就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围),并在图7所给的平面直角坐标系中画出此函数的图像。 (2)设此人在行进途中离B城的路程为s千米,行进时间为小时,就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围),并在图7所给的平面直角坐标系中画出此函数的图像。
附加题: (20 分)
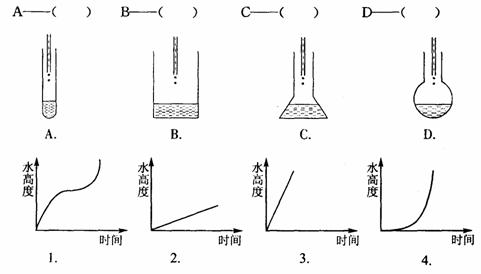
1.水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何
随着时间t变化的.请选择匹配的示意图与容器.(4分)
2.如图4所示,已知一次函数y=kx b(k≠0)的图象与x轴、y 轴分别交于A,B两点,且与反比例函数y= 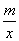 (m≠0)的图象在第一象限交于C点,CD⊥x轴, 垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于C点,CD⊥x轴, 垂足为D,若OA=OB=OD=1.
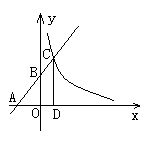 (1)求点A, B, D坐标. (1)求点A, B, D坐标.
(2)求一次函数和反比例函数的关系式.
(3)根据图象写出一次函数的值大于反比例
函数的值的x的取值范围。(9分)
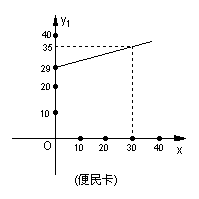
3.为发展电信事业,方便用户,A地电信公司对移动电话采用不同的收费方式,其中,所使用的“便民卡”和“如意卡”每月(30天)的通讯时间x(分钟)与通话费(y元)的关系如图.
(1) 分别求出通话费y1、y2与通话时间x之间的函数关系式。
(2) 在A地的林小姐预备购买一部移动电话,并决定选用“便民卡”和“如意卡”中的一种付费方式进行消费。请你帮助林小姐分析应选哪种卡合算。(7分)
温馨提示:网页上
|