|
一、选择题(3分×10=30分)请将所有答案的代号填入下表格内(不填者不给
分)
1、-3x<-1的解集是
A x< 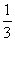 B x<-
B x<- 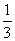 C x>
C x> 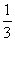 D x>-
D x>- 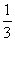
2、假如a>b,那么下列不等式不成立的是
A a-5>b-5 B -5a>-5b C 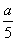 >
> 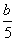 D -5a<-5b
D -5a<-5b
3、若4x² mxy 9y²是一个完全平方式,则m=
A 6 B 12 C ±6 D ±12
4、要使分式 
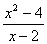 为零,那么x的值是
为零,那么x的值是
A -2 B 2 C ±2 D 0
5、分式 
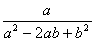 ,
, 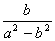 ,
, 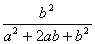 的最简公分母是( )
的最简公分母是( )
A (a²-2ab b²)(a²-b²)(a² 2ab b²) B (a b)²(a-b)²
C (a b)²(a-b)²(a²-b²) D 
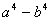
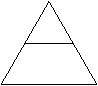
6、如图1,DE∥BC,则下列不成立的是( )
A 
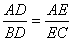 B
B 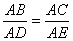 C
C 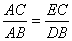 D
D 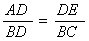
A
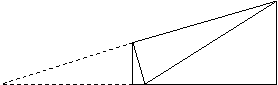
 7、如图2,∠1=∠B,AD=5㎝,AB=10㎝,则AC= 7、如图2,∠1=∠B,AD=5㎝,AB=10㎝,则AC=
D E
A 50㎝ B 2㎝ C 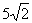 ㎝ D
㎝ D  ㎝
㎝
8、设S是数据 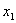 ,……,
,……, 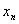 的标准差,Sˊ是
的标准差,Sˊ是 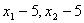 …… B 图1 C
…… B 图1 C
 , , 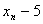 的标准差,则有: A
的标准差,则有: A
A S= Sˊ B Sˊ=S-5 C Sˊ=(S-5)² D Sˊ= 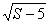 D 1
D 1
C
B 图2
9、假如三角形三个外角度数之比是3:4:5,则此三角形一定是( )
A 锐角三角形 B 直角三角形 C 钝角三角形 D 不能确定
10、m、n是常数,若mx n>0的解是x< 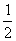 ,则nx-m<0的解集是( )
,则nx-m<0的解集是( )
A x>2 B x<2 C x>-2 D x<-2
二、填空题(3分×6=18分)
11、分解因式m(x-2y)- n(2y-x)=(x-2y)(______________)
12、(-x)²÷y·  =____________
=____________
13、若x:y:z=2:(-1):1,则 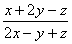 =____________
=____________
14、设C是线段AB的黄金分割点AB=4cm,则AC=_______________
15、若10个数据的平均数是 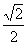 ,平方和是10,则方差是_____________
,平方和是10,则方差是_____________
16、一项工程,甲单独做5小时完成,甲、乙合做要2小时,那么乙单独做要_____小时。
三、解答下列各题
17、解不等式组,并在数轴上表示出来(6分)
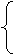 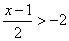
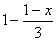 ≥x
≥x
18、分解因式(4分)
-3x³ 12x²-12x
19、先化简,后求值(9分)
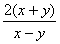 (x=3,y=2)
(x=3,y=2)
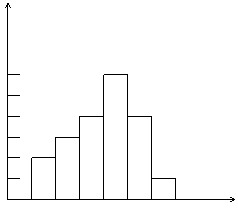
20、(9分)八年级某班进行小制作评选,作品上交时间为5月1日至30日,评委把同学上交作品的件数按5天一组分组统计绘制了频数直方图如图。已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12。
(1) 本次活动共有多少件作品参评?
(2) 哪组上交的作品数量最多?有多少件?
(3) 经过评选,第四组与第六组分别有10件与2件获奖,那么这两组中哪组的获奖率较高?
 频率 频率
6
5
4
3
2
1 日期
1 6 11 16 21 26 31
21、(6分)如图,AB∥EF,问∠A,∠C,∠1有何等量关系?证实你的结论。
A B
C
1
E D F
22、(8分)甲骑自行车从A地出发去距A地60km的B地,2.5h后乙骑摩托车也从A出发,到达B地10min后甲才到达,若乙的速度是甲速度的5倍,求甲、乙二人的速度。
23、(10分)如图,四边形ABCD中,AD⊥AB BC⊥AB BC=2AD DE⊥CD交AB边于E,连结CE。请找出DE、AE、CE之间的等量关系并加以证实。 C
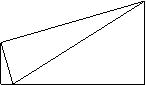
D
A B
E
参考答案(八年级数学)
一、题号 1 2 3 4 5 6 7 8 9 10
答案 C B D A B D C A B D
二、11、m n 12、 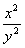 13、-
13、- 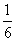
 14、2(
14、2( 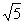 -1)cm或2(3-
-1)cm或2(3- 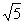 )
)
15、 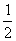 16、
16、 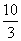
三、17、解:由① x>-3 ………………………1分
 由② x≤1 ………………………2分 由② x≤1 ………………………2分
   ∴原不等式组的解是-3<x≤1……3分 x ∴原不等式组的解是-3<x≤1……3分 x
-3 -2 -1 0 1
…………………6分
18、解:原式=-3x(x 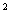 -4x 4)………………2分
-4x 4)………………2分
=-3x(x-2) 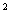 ………………4分
………………4分
19、解:原式= 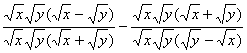 ……………………3分
……………………3分
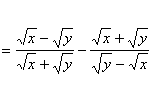 ………………………………………4分
………………………………………4分
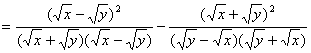
= 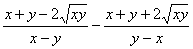 ……………………………5分
……………………………5分
= 
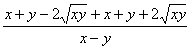 ………………………6分
………………………6分
= 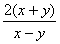 ………………………………………………7分
………………………………………………7分
当x=3,y=2时 原式= 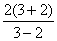 =10 …………………………………………9分
=10 …………………………………………9分
20、解(1)第三组的频率是 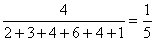 ……………………1分
……………………1分
12÷ 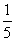 =60(件)……………2分 ∴共有60件作品参评 ………3分
=60(件)……………2分 ∴共有60件作品参评 ………3分
(2)由图可知,第四组作品数量最多 ………………………………1分
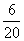 ×60=18(件) ………………………………2分
×60=18(件) ………………………………2分
∴第四组共有作品18件 …………………………3分
(4) 第四组获奖率是 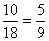 ……………………………1分
……………………………1分
第六组获奖率是 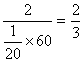 ……………………2分
……………………2分
∵ 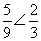 ∴第六组的获奖率较高 ………………………3分
∴第六组的获奖率较高 ………………………3分
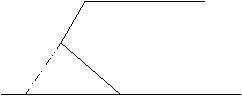
21、解:等量关系为:∠A ∠C-∠1=180°……………………………1分
证实:延长AC交EF于G,则∠ACD=∠2 ∠1(三角形外角定理)……2分
∵AB∥EF ∴∠A ∠2=180°(两直线平行,同旁内角互补)…………4分
∠2=180°-∠A 代入 ∠ACD=180°-∠A ∠1
即∠A ∠C-∠1=180°……………………………………6分
(亦可过C作AB的平行线,请按步给分)
 A B A B
C
2 1
G E D F
22、解:设甲速为xkm/h,则乙速为5xkm/h ……………………1分
依题意得 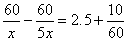 ………………………4分
………………………4分
解之得x=18 …………………………………………6分
经检验x=18是原方程的根……………………………7分
∴5x=90
答:甲、乙两人速度分别是18km/h,90km/h.……………………8分
23、解:关系式DE 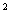 =AE·CE …………………………2分
=AE·CE …………………………2分
证实 延长BA、CD交于O ………………………3分
∵AD⊥AB BC⊥AB ∴AD∥BC(同位角相等,两直线平行)
∴△ODA∽△OCB
∴ 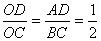 (相似三角形对应边成比例) 即 OD=DC……………5分
(相似三角形对应边成比例) 即 OD=DC……………5分
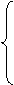 在△EDO与△EDC中 在△EDO与△EDC中
OD=DC
∠EDO=∠EDC=90°
ED=ED
∴ △EDO≌△EDC(SAS)……………………………………7 分
∴∠O=∠1
又∵∠O ∠AED=∠ADE ∠AED=90°(互余)
∴∠O=∠ADE
∴∠1=∠ADE ……………………………8分
∴Rt△DAE∽Rt△CDE …………………9分
∴ 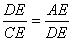 (相似三角形对应边成比例)
(相似三角形对应边成比例)
即 DE 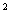 =AE·CE ……………………………10分
=AE·CE ……………………………10分
C
 1 1
D
O A E B
翠园初中 曹尔乔
|