|
班级_______ 姓名________ 成绩________
一、选择题:在下面四个选项中只有一个是正确的.(本题共18分,每小题3分)
1.下列计算正确的是( )
A. 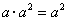 B.
B. 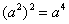
C. 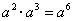 D.
D. 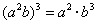
2.若m是非负数,则用不等式表示正确的是( )
A.m<0 B.m>0 C.m≤0 D.m≥0
3.下列图形中是轴对称图形,但不是中心对称图形的是( )
A.等腰三角形 B.平行四边形
C.菱形 D.正方形
4.下列式子中,从左到右的变形是因式分解的为( )
A. 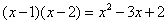
B. 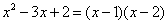
C. 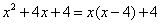
D. 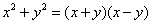
5.在布袋中装有两个大小一样,质地相同的球,其中一个为红色,一个为白色.模拟“摸出一个球是白球”的机会,可以用下列哪种替代物进行实验( )
A.“抛掷一枚普通骰子出现1点朝上”的机会
B.“抛掷一枚啤酒瓶盖出现盖面朝上”的机会
C.“抛掷一枚质地均匀的硬币出现正面朝上”的机会
D.“抛掷一枚普通图钉出现针尖触地”的机会
6.如图,△ 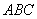 与△
与△ 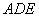 都是等腰直角三角形,∠C=∠AED=90°,点E在AB上,假如△ABC绕点A逆时针旋转后能与△ADE重合,则旋转角度是( )
都是等腰直角三角形,∠C=∠AED=90°,点E在AB上,假如△ABC绕点A逆时针旋转后能与△ADE重合,则旋转角度是( )
A.90° B.60° C.45° D. 30°
二、填空题:(本题共24分,每小题3分)
7.计算:  =__________________________________.
=__________________________________.
8.分解因式: 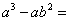 ___________________________________.
___________________________________.
9.如图所示,图形①经过________________
变换得到图形②;图形②经过_____________
变换得到图形③;图形③经过______________
变换得到图形④.(填平移、旋转或轴对称)

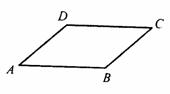
10.如图,在□ABCD中,∠A=40°则∠B=________度,∠C=_________度,∠D=_________度.
11.不等式组 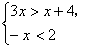 的解集为______________________________________.
的解集为______________________________________.
12.如图,已知菱形ABCD,AC与BD交于O,AO=3cm,BO=4cm,则菱形ABCD的面积为_________ 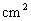 .
.
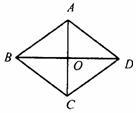
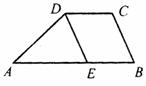
13.如图,梯形ABCD中,AB∥DC,DE∥CB,△AED的周长为16,EB=3,则梯形ABCD的周长为_________.
14.已知关于x的方程 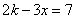 的解是正数,则k的取值范围是_____________.
的解是正数,则k的取值范围是_____________.
三、解答题:解答题应写出必要的解题步骤.(本题共58分)
15.(本题4分)解不等式: 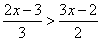 ,并在数轴上表示出它的解集.
,并在数轴上表示出它的解集.
解:

16.(本题4分)先化简,再求值.
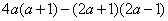 ,其中
,其中 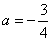 .
.
解:
17.(本题4分)(保留作图痕迹)如图,已知AB=DC.
(1)画出线段AB平移后的线段DE,其平移方向为射线AD的方向,平移的距离为线段AD的长.
(2)连续CE,并指出∠DEC与∠DCE之间的大小关系.
解:(1)
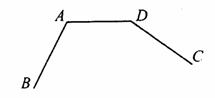
(2)答:∠DEC________∠DCE.
18.(本题4分)在一次大规模英文文献的统计中,发现英文字母A出现的机会在0.091左右.假如这次调查是可信的,那么再去统计一篇约为300字的英文文献,可以说字母A出现的频率会非常接近9.1%吗?为什么?
答:
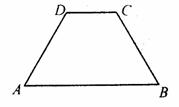
19.(本题4分)如图,在等腰梯形ABCD中,AB∥DC,AB=8,DC=3,∠A=60°,求CB的长.
解:
20.(本题5分)如图,在矩形ABCD中,M是对角线AC上的一个动点(M与A、C点不重合),作ME⊥AB于E,MF⊥BC于F.
(1)试说明四边形EBFM是矩形;
(2)连结BM.当点M运动到使∠ABM为何值时,矩形EBFM为正方形?请写出你的结论.
解:(1)
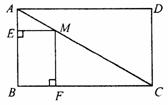
(2)答:当点M运动到使∠ABM=__________度时,矩形EBFM为正方形.
21.(本题5分)现有45本书分给若干个课外小组,若每组分7本有剩余,若每组分9本不够分,问共有多少个课外小组?
解:
22.(本题6分)已知 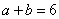 ,
, 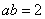 .
.
(1)求 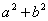 的值;
的值;
(2)求 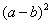 的值.
的值.
解:
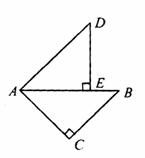
23.(本题4分)已知△ABC,∠ACB=90°.把△ABC用直线分割成两部分,可以拼成与△ABC等面积的一些四边形.比如图①,把△ABC用直线EF分割后,利用中心对称知识,拼成了与它等面积的矩形GBCF.请你也利用中心对称知识,按下列要求进行操作:
(1)把图②中的直角△ABC用适当的直线分割成两部分,拼成与△ABC等面积的一个平行四边形;
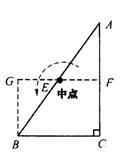
图①
(2)把图③中的直角△ABC用适当的直线分割成两部分,拼成与△ABC等面积的一个梯形.(图中需作必要的标记,不要求说明理由)
解:
(1) (2)
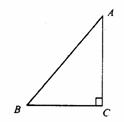 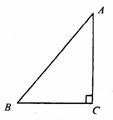
图② 图③
24.(本题5分)
先阅读下列因式分解的过程,再回答所提出的问题:
例1 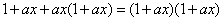
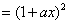 ;
;
例2 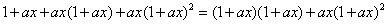
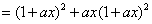
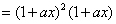
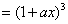 .
.
(1)分解因式: 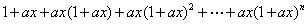 =______________;
=______________;
(2)分解因式: 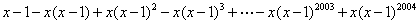 .
.
(答题要求:请将第(1)问的答案填写在题中的横线上)
解:(2)
25.(本题6分)
利用图形面积可以解释代数恒等式的正确性,也可以解释不等式的正确性.
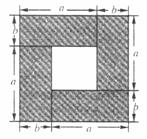
(1)根据下列所示图形写出一个代数恒等式;
(2)已知正数a,b,c和m,n,l,满足 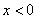 .试构造边长为k的正方形,利用图形面积来说明
.试构造边长为k的正方形,利用图形面积来说明 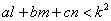 .
.
解:
26.(本题7分)
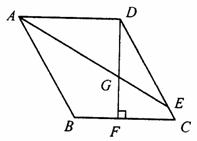
如图,已知□ABCD,AE平分∠BAD,交DC于E,DF⊥BC于F,交AE于G,且DF=AD.
(1)试说明 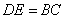 ;
;
(2)试问AB与DG+FC之间有何数量关系?写出你的结论,并说明理由.
解:
参考答案
一、选择题:(本题共18分,每小题3分)
1.B 2.D 3.A 4.B 5.C 6.C
二、填空题:(本题共24分,每小题3分)
7. 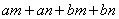 8.
8. 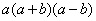 9.轴对称、平移、旋转(每空各1分)
9.轴对称、平移、旋转(每空各1分)
10.140,40,140 (每空各1分) 11. 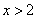 12.24 13.22 14.
12.24 13.22 14. 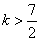
三、解答题:(本题共58分)(说明:与参考答案不同,但解答正确,相应给分)
15.(本题4分)去分母正确1分;整理1分;得出解集 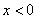 1分;在数轴上画出解集1分
1分;在数轴上画出解集1分
16.(本题4分)单乘多正确1分,运用平方差公式(或多乘多)正确1分,化简得正确结果 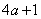 1分;代入求得正确结果-2 1分.
1分;代入求得正确结果-2 1分.
17.(本题4分)(1)(2分)说明:平移辅助线画实线不扣分,如未画辅助线,但标明平行和相等符号不扣分,未标明扣1分 (2)(2分)连结 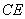 1分,填“=”1分.
1分,填“=”1分.
18.(本题4分)不可以这样说 2分;因为统计一篇约300字的英文文献的实验次数不够大,当实验次数不够大时,频率不一定非常接近大规模统计中所发现的机会 2分.(意思相近不扣分)
19.(本题4分)作辅助线 1分;说明平行四边形 1分;说明等边三角形 1分;求得 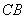 =5 1分.
=5 1分.
20.(本题5分,第(1)问3分,第(2)问2分) (1)说明四边形  是平行四边形2分,再说明是矩形1分(或说明有三个直角各1分,再说明是矩形1分). (2)45 2分.
是平行四边形2分,再说明是矩形1分(或说明有三个直角各1分,再说明是矩形1分). (2)45 2分.
21.(本题5分)正确列式 2分;正确求得解集 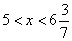 1分;求得符合条件的正整数解
1分;求得符合条件的正整数解 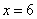 1分,答 1分.
1分,答 1分.
22.(本题6分,每小题3分)(1)正确运用完全平方公式变形1分,代入1分,求得 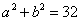 1分.(2)正确运用公式变形1分,代入1分,求得
1分.(2)正确运用公式变形1分,代入1分,求得 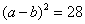 1分.
1分.
23.(本题4分)两图各2分;图中没有标记点中点,累计扣1分,未利用中心对称扣1分.
参考图:
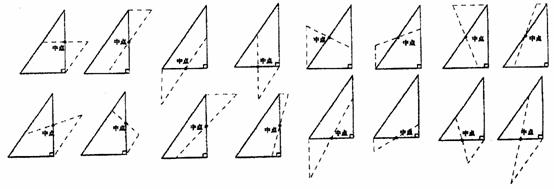
24.(本题共5分,第(1)问2分,第(2)问3分)
(1) 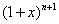 ……………………………………………………………………………2分
……………………………………………………………………………2分
(2) 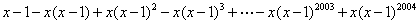
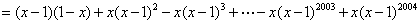 ……………3分
……………3分
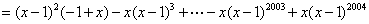 ……………………4分
……………………4分
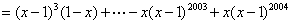

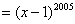 ……………5分(若整体反复提取公因式前两步各1分,最后结果1分)
……………5分(若整体反复提取公因式前两步各1分,最后结果1分)
25.(本题6分,第(1)问2分,第(2)问4分)
(1)比如: 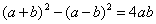 或
或 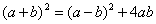 或
或 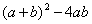 等
等
…………………………………………………2分
(2)比如构造如图所示正方形:(若画成 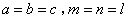 等非凡情况扣1分)
等非凡情况扣1分)
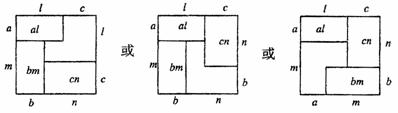 等……………5分 等……………5分
因为 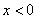 ,显然有
,显然有 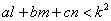 ………………………6分
………………………6分
26.(本题共7分,第(1)问3分,第(2)问4分)
(说明:此题重点考查对图形的熟悉与图形变换的意识,经过平移还原为正方形,即是一道典型成题.推理若利用平移、旋转知识未说明三点共线不扣分,用截长法相应给分)
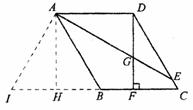
(1)因为四边形 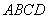 是平行四边形,
是平行四边形,
所以 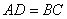 ,AB∥DC.
,AB∥DC.
所以∠BAE=∠DEA.……………………………………………………………………1分
因为AE平分∠BAD,
所以∠BAE=∠DAE.……………………………………………………………………2分
所以∠DEA=∠DAE.
所以AD=DE.
所以DE=BC.……………………………………………………………………………3分
(2) 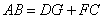 .…………………………………………………………………4分.
.…………………………………………………………………4分.
因为四边形 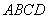 是平行四边形,
是平行四边形,
所以 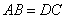 ,
, 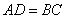 ,AB∥DC,AD∥BC.所以∠ABC+∠C=180°
,AB∥DC,AD∥BC.所以∠ABC+∠C=180°
把△DFC沿射线DA方向平移,平移距离为AD,则DC与AB重合,记平移后的三角形为△ABH,则∠AHB=∠DFC=90°,∠ABH=∠C,AH=DF,HB=FC.
因为∠ABH+∠ABC=∠C+∠ABC=180°,所以F,B,H三点共线.
所以 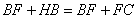 ,从而
,从而 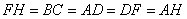 .
.
所以四边形 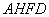 为正方形.阶段 …………………………………………………5分
为正方形.阶段 …………………………………………………5分
所以∠ADF=90°,AH∥DF.
把△ADG绕点A顺时针旋转90°,则 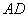 与
与 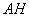 重合,∠DAG=∠HAI,∠DGA=∠HIA,∠AHI=∠ADG=90°.
重合,∠DAG=∠HAI,∠DGA=∠HIA,∠AHI=∠ADG=90°.
所以∠AHB+∠AHI=∠AHB+∠ADG=180°,所以I,H,B三点共线.…………6分
因为AE平分∠BAD,所以∠BAG=∠DAG.
所以∠HAB+∠BAG=∠HAB+∠DAG=∠HAB+∠HAI.
即 ∠HAG=∠IAB.
因为AH∥DF,所以∠HAG=∠DGA.
所以∠BIA=∠DGA=∠BAI.所以 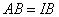 .
.
因为 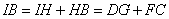 ,所以
,所以 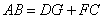 .…………………………7分.
.…………………………7分.
|