|
班别 姓名 座号 成绩
一、填一填(每题3分,共30分)
1、当x=____________时,分式 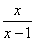 无意义;当x=________时,分式
无意义;当x=________时,分式 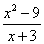 的值为零.
的值为零.
2、科学家发现一种病毒的直径为0.000043米,用科学记数法表示为_________________米.
3、反比例函数 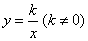 的图象经过P,如图1所示,根据图象可知,反比例函数的解析式为_________________.
的图象经过P,如图1所示,根据图象可知,反比例函数的解析式为_________________.
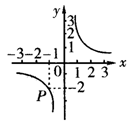
图1
4、等腰三角形的腰长为10,底边上的高为6,则底边的长为__________ .
5、在直角  ABC中,
ABC中, 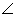 C=90°,c=20,b=15,则a=__________ .
C=90°,c=20,b=15,则a=__________ .
6、一项工程,甲单独做x小时完成,乙单独做y小时完成,则两人一起完成这项工程需要__________ 小时。
7、 平行四边形两个邻角的平分线互相______ ,两个对角的平分线互相______ (填“平行”或“垂直”)、
8、已知一组数据的平均数为a,方差为b,那么一组数据小x1 1,x2 1,…,xn 1的平均数和方差分别是 .
9、若梯形的上底长为6cm,中位线长8cm,则此梯形的下底线长 cm;连结两条对角线的中点的线段长 cm。
10、若关于x的分式方程 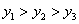 无解,则m的值为__________.
无解,则m的值为__________.
二、选择题:(每题3分,共15分)
1、下列计算正确的是( )
A. 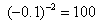 ; B.
; B. 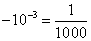 ; C.
; C. 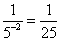 ; D.
; D. 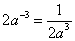
2、若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数 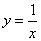 的图象上,则下列结论中正确的是( )
的图象上,则下列结论中正确的是( )
A. 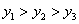 ; B.
; B. 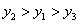 C.
C. 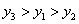 D.
D. 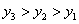
3、下列几组数中,不能作为直角三角形三边长度的是 ( )
A. a=7, b=24, c=25 B. a=1.5, b=2, c=2.5 C. a= 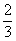 , b=2, c=
, b=2, c= 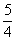 D. a=15, b=8,c=17
D. a=15, b=8,c=17
4、下列各分式中,最简分式是( )
A、 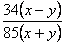 B、
B、 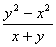 C、
C、 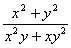 D、
D、 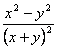
5、在平行四边形ABCD中,EF过对角线的交点O,若AB=4,BC=7,OE=3,则四边形EFCD周长是( )
A.14 B. 11 C. 10 D. 17
三、解答题:
1、(6分)计算: 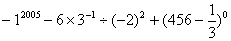
(6分)(2) 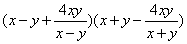
2、(7分)解分式方程 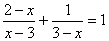
3、(6分)如图,E、F为平行四边形ABCD对角线AC延长线上的点,且AE=CF,连结BF、BE、DF、DE。求证:BEDF是平行四边形。

 4、(6分)如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理? 4、(6分)如图,在边长为c的正方形中,有四个斜边为c的全等直角三角形,已知其直角边长为a,b.利用这个图试说明勾股定理?
5、(8分)如图,已知正方形ABCD,延长BC到E,在CD上截取CF=CE,延长BF交DE于G. 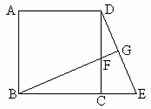 求证:BG⊥DE. 求证:BG⊥DE.
6、画出反比例函数 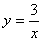 的图象,并写出图象的性质.(7分)
的图象,并写出图象的性质.(7分)
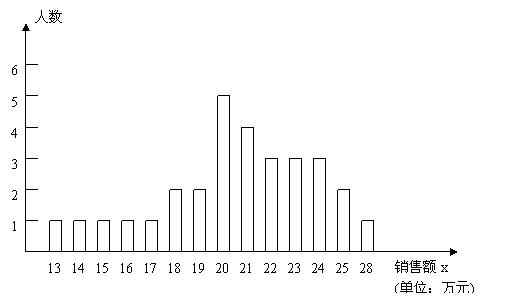 四、(9分)某商场统计了每个营业员在某月的销售额,统计图如下: 四、(9分)某商场统计了每个营业员在某月的销售额,统计图如下:
解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当时为不称职,当时,为基本称职,当为称职,当时为优秀。试求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比,并用扇形图统计出来。
(2)根据(1)中规定,所有称职和优秀的营业员月销售额的中位数、众数和平均数分别是多少?
(3)为了调动营业员的工作积极性,决定制定月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励,假如要使得称职和优秀的所有营业员的半数左右能获奖,你认为这个奖励标准应定为多少元合适?并简述其理由。
|