八年级数学（下）第一学月数学试卷

考试时间：120分钟 满分：150分

命题人：南川一中 余华君

一、填空题：（每题4分，共48分）

2、写出一个不等式，使它的解集是x＞－1　　　 　

3、不等式6－2x＞0的解集是_ __ _____.

4、24m2n＋18n的公因式是__________;

5、分解因式：2x3－8x2＝ 　 　 ， x2－14x＋49＝ ，

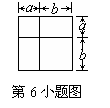
6、观察图形，根据图形面积的关系，不需要连其他的线，便可以得到一个用来分解因式的公式，这个公式是 。

7、不等式 EQ \F(x 5,2) －1＞ EQ \F(3x 2,3) 的解集为__________________。

8、当x　　　时，分式 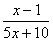的值为零；当x　　　　时，分式 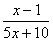有意义。

9、化简： ＝　　　 ， ＝ 　　　 。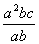

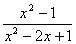10、当x______ __时，代数式 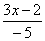的值是非正数.？

11、若x= 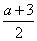，y= 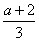，且x＞2＞y，则a的取值范围是___ _____.。

12、不等式组 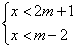的解集是x＜m－2，则m的取值应为___ _____.。

二、选择题：（每小题4分，共40分）

1、假如a＞b ，下列各式中不正确的是……………( )

A、a－3＞b－3 B、 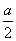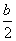＞ C、－2a＜－2b D、－2a＞－2b

2、下列从左到右的变形，是因式分解的是（ ）

A、(a＋3)(a－3)=a2－9 B、x2＋x－5=(x－2)(x＋3)＋1

C、a2b＋ab2=ab(a＋b) D、x2＋1=x(x＋ )

3、在 、 、 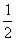、 、 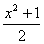、 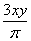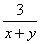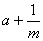中分式的个数有（ ）

A、2个 B、3个 C、4个 D、5个

4、如图，用不等式表示数轴上所示的解集，正确的是（ ）

A、x＜－1或x≥－3 B、x≤－1或x＞3 C、－1≤x＜3 D、－1＜x≤3

5、下列说法①x＝0是2x－1＜0的解；②x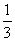＝ 不是3x－1＞0的解；

③－2x－1＜0的解集是x＞2；④不等式 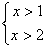的解集是x＞1，

其中正确的个数是……( )

A、1个 B、2个 C、3个 D、4个

6、下列多项式中不能用平方差公式分解的是（ ）

A、a2－b2 B、－x2－y 2 C、49x2－ y2z2 D、16m4n2－25p2

7、下列多项式能用完全平方公式分解的是（　　　）

A、x2－2x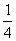－ B、(a＋b)(a－b)－4ab C、a2＋ab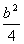＋ 　 D、y2＋2y－1

8、分解因式b2(x－3)＋b(x－3)的正确结果是（ ）

A、(x－3) (b2＋b) B、b(x－3) (b＋1)

C、(x－3) (b2－b) D、b((x－3) (b－1)

9、把分式 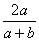分子、分母中a、b都变成原来的2倍，则分式的值变为原分式值的( )

A、4倍 B、2倍 C、不变 D、 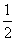倍

10、已知点A（2－a，a＋1）在第一象限，则a的取值范围是（ ）

A、a＞2 B、－1＜a＜2 C、a＜－1 D、a＜1

三、把下列各式因式分解：（每小题4分，计16分）

①7x2－63＝ ②9－12t＋4t2 ＝

③－2x3＋4x2－2x＝ ④(a2＋4)2 －16a2＝

四、解答题（每题6分，共24分，要写出解题过程，直接写答案不得分）

1、 解不等式2－x≥2(x－3)，并写出非负整数解。

2、解下列不等式组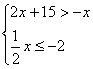， 并把解集表示在数轴上表示出来：　　　　　　　　　　　　　　

3、先化简再求值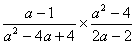： ，其中a=－1

4、已知方程组 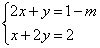的解x、y满足x＋y＞0，求m的取值范围.

五、应用题（共22分）

1、某商场文具部的某种毛笔每支售价25元，书法练习本每本售价5元。该商场为促销制定了如下两种优惠方式：第一种：买一支毛笔附赠一本书法练习本；第二种：按购买金额打九折付款。八年级（5）班的小明想为本班书法爱好小组购买这种毛笔10支，书法练习本 x（x≥10）本。试问小明应该选择哪一种优惠方式才更省钱？（要求利用一次函数与不等式（组）的知识进行解答）（10分）

2、某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品，共50件，已知生产一件A种产品，需用甲种原料9千克、乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克、乙种原料10千克，可获利润1200元．

　　(1)按要求安排A、B两种产品的生产件数，有哪几种方案？请你给设计出来；

　　(2)设生产A、B两种产品获总利润是y(元)，其中A种的生产件数是x，试写出y与x之间的函数关系式，并利用函数的性质说明(1)中的哪种生产方案获总利润最大？最大利润是多少？（12分）