八年级数学上学期期中试卷
(满分:100分,时间:120分钟, 版本:人教版)
一、填空题(每空1分,共22分)
1、若函数y= (k-1)x|k|是正比例函数,则k= .
2、在公式s=50t中常量是_______,变量是________。
3、已知一次函数y=2x 4的图像经过点(m,8),则m=________。
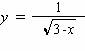 4、函数 中,自变量x的取值范围是_____________。
4、函数 中,自变量x的取值范围是_____________。
5、 周长为
6、 汽车行驶前,油箱中有油
7、一个正比例函数 ![]()
8、利用函数y=x+4的图像,当自变量x______时,x+4=0;当x_______时,x+4>0。
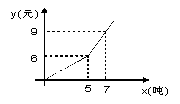 9、我国很多城市水资源缺乏,为了加强居民的节水 意识,某自来水公司采取分段收费标准,某市居民每月交水费y(元),与水量x(吨)的函数关系如右图所示,请你通过函数图像,回答自来水公司收费标准:若用水不超过5吨,水费为_______元/吨;若用水超过5吨,超过部分的水费为_____元/吨。
9、我国很多城市水资源缺乏,为了加强居民的节水 意识,某自来水公司采取分段收费标准,某市居民每月交水费y(元),与水量x(吨)的函数关系如右图所示,请你通过函数图像,回答自来水公司收费标准:若用水不超过5吨,水费为_______元/吨;若用水超过5吨,超过部分的水费为_____元/吨。
10、在整理数据时,常用的统计图有__________,__________,________,_________.
11、在数“16266366646666566666”中数字“
12、要反映出下列三个问题中的数据,你认为最适宜的统计图:
(1)
(2)北京市统计局调查显示:2003年1-9月份,北京、天津、上海、广州、重庆五市农民人均收入分别为5567元、5423元、5802元、4889元、1454元。该题应选______________统计图。
(3)生活垃圾中,直接填埋的占23%,焚烧的占73%,回收利用的占40%,该题应选______________统计图。
命题人:张彩华
二、选择题(每小题2分,共18分)
13、下列说法正确的是( )
A、 一次函数是正比例函数 B、正比例函数是一次函数
C、 正比例函数不是一次函数 D、一次函数不可能是正比例函数
14、把直线y=-4x通过平移得到直线y=-4x-6,则直线y=-4x必须( )
A、向上平移6个单位 B、向下平移6个单位
C、向左平移6个单位 D、向右平移6个单位
|
X |
|
0 |
|
Y |
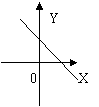 15、一次函数y=kx+b的图像如图所示,则k,b的符号分别是( )
15、一次函数y=kx+b的图像如图所示,则k,b的符号分别是( )
A、k>0,b>0 B、k>0,b<
16、下列函数 (1)y=2x-1(2)y=πx (3)y= EQ \F(1,x) (4) D. y= ![]()
(5)y=x2-1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个 (15题)
17、已知点(-1,y1),(2,y2)都在直线y= -3x+1上,则y1 ,y2大小关系是( )
A.y1 >y2 B.y1 =y
18、下列有关频数分布表和频数分布直方图的理解,正确的是( )
A、频数分布表能清楚地反映事物的变化情况
B、频数分布直方图能清楚地反映事物的变化情况
C、频数分布直方图能清楚地表示出各部分在总体中所占的百分比
D、二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目
|
x |
|
y |
|
O |
|
x |
|
y |
|
O |
|
x |
|
y |
|
O |
|
x |
|
y |
|
O |
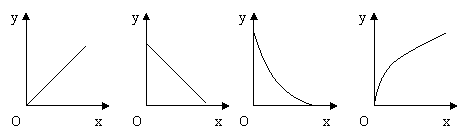 19、下图是一种古代计时器------“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间,用x表示时间, y表示壶底到水面的高度,下面的哪个图像适合表示一小段时间内y与x的函数关系(暂不考虑水量变化对压力的影响)?( )
19、下图是一种古代计时器------“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间,用x表示时间, y表示壶底到水面的高度,下面的哪个图像适合表示一小段时间内y与x的函数关系(暂不考虑水量变化对压力的影响)?( )
A B C D
20、有一组数据,最小的为40,最大的为89,现在把它们分组,组距为10,则可分为( )
A、4组 B、5组 C、7组 D、8组
21、如图所示是某公司近三年的资金投放总额与利润统计示意图,根据图中的信息判定:
(1)2001年的利润比2000年的利润率高2%
(2)2002年的利润比2001年的利润率高8%
(3)这三年的利润率约为14%
(4)这三年中2002年的利润率最高。
![]()
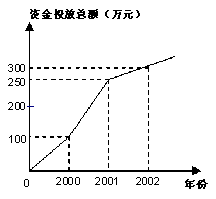

其中正确的结论共有( )
A、1个 B、2个 C、3个 D、4个
三、解答题(共60分)
22、[10分]已知一次函数图像经过(1, -1)和(-2,-7)两点,
(1)求此一次函数解析式(2分)
(2)画出此函数的图像,并说出该图象的性质(至少两条)(4分)
(3)求该图象与x,y轴交点坐标(2分)
(4)求该图象与坐标轴围成的三角形的面积(2分)
23、[6分] 为了保护学生的视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度.
第一套
第二套
椅子高度x(cm)
40.0
37.0
桌子高度y(cm)
75.0
70.0
(1) 请确定y与x的函数关系式(不要求写出x的取值范围);(3分)
(2) 现有一把高
24、[8分]向阳中学八年级(8)班就学生的上学方式作了调查,得到的数据如下,
请根据表回答下列问题
方式
步行
骑自行车
坐公共汽车
其它
人数
25
8
13
4
(1)八年级(8)班共有多少名学生?(2分)
(2)请你设计一种统计图来描述该班同学的上学方式。(4分)
(3)从你绘制的统计图中可以获得哪些信息?试写出两条信息。(2分)
25、[10分]某班60人的期末成绩(成绩为整数)的频率分布表如下,请根据表中信息
填空:
分组
频数
频率
49.5-59.5
3
0.05
59.5-69.5
9
m
69.5-79.5
24
0.40
79.5-89.5
18
0.30
89.5-99.5
n
0.10
合计
60
1.00
(1) 在表中,成绩在69.5-79.5分范围内的频数是_________;(2分)
(2) 在表中,频率m=__________,频数n=____________;(2分)
(3) 根据频数分布表绘制出相应的频数分布直方图(4分)
(4) 成绩优秀的学生有________人(成绩大于或等于80分为优秀)。(2分)
26、[8分]我们曾经考虑过下面的两种移动电话计费方式:
神州行
全球通
月租费
0
50元/月
本地通话费
0.60元/分钟
0.40元/分钟
用函数方法解答如何选择计费方式更省钱?
27、[10分]已知A(8,0)及在第一象限的动点P(x,y),且x+y=10,
设△OPA的面积为S
(1)求S关于x的函数表达式;(3分)
(2)求x的取值范围;(2分)
(3)求S=12时P点坐标;(2分)
(4)画出函数S的图像。(3分)
28、[8分]:某公司在甲市和乙市分别有库存的某 种机器12台和6台,现销售给A市10台,B市8台,已知从甲市调动一台到A市、B市的运费分别是400元和800元,从乙市调一台到A市、B市的运费分别是300元和500元。
(1)设从甲市调往A市x台,求总运费y关于x的函数解析式及自变量的取值范围;(4分)
(2)求出总运费最低的调运方案及最低的运费。(4分)
