|
八年级数学上学期月考试题
一、选择题。(本题共9小题,每小题4分,共36分).
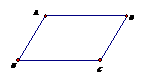 1、下列哪组条件能判别四边形ABCD是平行四边形?( ) 1、下列哪组条件能判别四边形ABCD是平行四边形?( )
A、AB∥CD,AD=BC B、AB=CD,AD=BC
C、∠A=∠B,∠C=∠D D、AB=AD,CB=CD
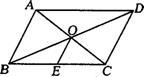 2、如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( ) 2、如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )
A.3 cm B.6 cm C.9 cm D.12 cm
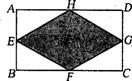 3、已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为 ( ) 3、已知:如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为 ( )
 A.8 B.6 C.4 D.3 A.8 B.6 C.4 D.3
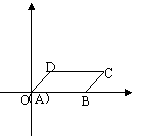
4、如图,在平面直角坐标系中,□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0)(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
 5、如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若用x、y表示小矩形的两边长(x>y),请观察图案,指出以下关系式中不正确的是 ( ) 5、如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若用x、y表示小矩形的两边长(x>y),请观察图案,指出以下关系式中不正确的是 ( )
A. 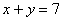 B.
B. 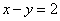
C. 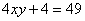 D.
D. 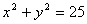
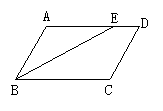 6、如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( ) 6、如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于( )
A.18° B.36° C.72° D.108°
 7、下列四个命题中,假命题是( ). 7、下列四个命题中,假命题是( ).
A 等腰梯形的两条对角线相等
B 顺次连结四边形的各边中点所得的四边形是平行四边形
C 菱形的对角线平分一组对角
D 两条对角线互相垂直且相等的四边形是正方形
8、等腰梯形的腰长为13cm,两底差为10cm,则高为 ( )
A、 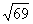 cm B、12cm C、69cm D、144cm
cm B、12cm C、69cm D、144cm
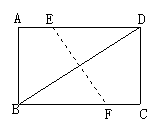
9.如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠, 使B点与D点重合,则折痕EF的长为( )
A. 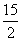 \* MERGEFORMAT
B.
\* MERGEFORMAT
B. 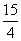 \* MERGEFORMAT
C.5 D.6
\* MERGEFORMAT
C.5 D.6
二、填空题(本题共5小题,每小题4分,共20分).
10.如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,则∠AEG和∠EGB的度数分别为____________________.
11、如图,在□ABCD中,已知对角线AC和BD相交于点O,△ABO的周长为15,AB=6,那么对角线AC+BD= 。
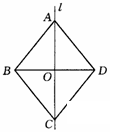 12、如图,l是四形形ABCD的对称轴,假如AD∥BC,有下列结论:①AB∥CD ②AB=BC ③AB⊥BC ④AO=OC其中正确的结论是 。(把你认为正确的结论的序号都填上) 12、如图,l是四形形ABCD的对称轴,假如AD∥BC,有下列结论:①AB∥CD ②AB=BC ③AB⊥BC ④AO=OC其中正确的结论是 。(把你认为正确的结论的序号都填上)
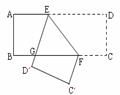 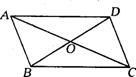
(第10题图) (第11题图) (第12题图)
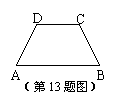 13、在梯形ABCD中,AB//CD,∠D=2∠B, 13、在梯形ABCD中,AB//CD,∠D=2∠B, 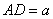 ,
, 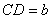 ,则AB的长为 。
,则AB的长为 。
14、对角线长为2 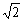 \* MERGEFORMAT
的正方形的周长为___________,面积为__________。
\* MERGEFORMAT
的正方形的周长为___________,面积为__________。
三、解答题。(本题共5小题,每小题7分,共35分,解答应写出文字说明、证实过程或演算步骤)
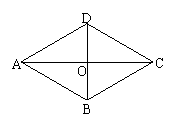 14(7分)、如图,在菱形ABCD中,AB=BD=5, 14(7分)、如图,在菱形ABCD中,AB=BD=5,
求:(1)∠BAC的度数;(2)求AC的长。
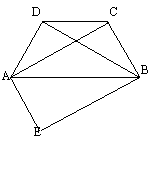
15(7分)如图,已知四边形ABCD是等腰梯形, CD//BA,将△ABD沿AB对折得到△ABE,求证:四边形AEBC是平行四边形。
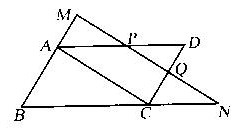 17(9分)、已知:如图,AC是□ABCD的对角线,MN∥AC,分别交AD、CD于点P、Q,试说明MP=QN。 17(9分)、已知:如图,AC是□ABCD的对角线,MN∥AC,分别交AD、CD于点P、Q,试说明MP=QN。
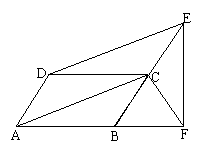
18(10分)、已知:如图,四边形ABCD是平行四边形,DE//AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF。
19(10分)、已知如图,四边形ABCD、四边形DEBF都是矩形,AB=BF,BE、AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形。

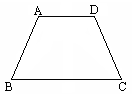
4.(7分)、已知:如图,在四边形ABCD中,∠B=∠C,AB与CD不平行,且AB=CD.求证:四边形ABCD是等腰梯形.
五、解答题。(本题共3小题,20、21题各12分,22题13分,共37分.解答应写出文字说明、证实过程或演算步骤)
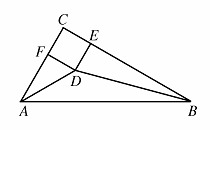
20、(12分)如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证: 四边形CFDE是正方形.
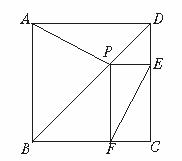
21、(12分)、已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足,求证:AP=EF.
|