|
八年级上学期期末测试卷
班级_______ 姓名________ 成绩________
一、填空题(3分×8=24分)
1.若多项式ax2- 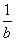 可分解为(3x
可分解为(3x 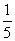 )(3x-
)(3x- 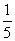 ),则a=__________,b=__________.
),则a=__________,b=__________.
2.若多项式-9x2 2x a是完全平方式,则a=__________.
3.当x__________ 时,分式 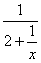 有意义.
有意义.
4.a,b,c为△ABC的三边,且分式 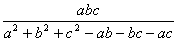 无意义,则△ABC为____三角形.
无意义,则△ABC为____三角形.
5.已知: 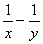 =3,则
=3,则 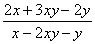 =__________.
=__________.
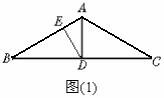
6.如图(1),AB=AC,∠BAC=120°,D是BC的中点,DE ⊥AB垂足为E,若AD=3 cm,则AB=__________ cm,AE=__________ cm.
7.在角,等边三角形、直角三角形,正方形这四个图形中有__________个轴对称图形,其中对称轴最多的是__________,有__________条对称轴.
8.两根木棒的长分别是8 cm ,10 cm,要选择第三根木棒将它们钉成一个三角形,那么第三根木棒长x的范围是________ ,假如以5 cm为等腰三角形的一边,另一边为10 cm,则它的周长应为__________.
二、选择题(3分×8=24分)
9.到△ABC的三个顶点距离相等的点是△ABC的
A.三条中线的交点 B.三条角平分线的交点
C.三条高的交点 D.三条边的垂直平分线的交点
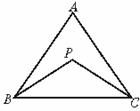
10.如图(2),△ABC中,AB=AC,A=50°,P是△ABC内一点,且∠PBC=∠PCA,则∠BPC的度数等于
A.100° B.115° C.130° D.140°
图(2) 图(3) 图(4)
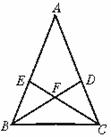
11.如图(3)所示,在△ABC中,AB=AC,A=36°,BD、CE分别为∠ABC与∠ACB的角平分线且相交于点F,则图中的等腰三角形有
A.6个 B.7个 C.8个 D.9个
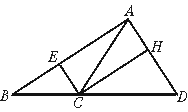
12.如图(4),CE平分∠ACB,CD=CA,CH⊥ AD于H,则∠ECA与∠HCA的关系是
A.相等 B.和等于90°
C.和等于45° D.和等于60°
13.下列分式中是最简分式的是
A. 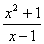 B.
B. 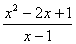 C.
C. 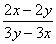 D.
D. 
14.下列多项式中,不含(x-1)因式的是
A.x3-x2 1-x B.x y-xy-x2
C.x2-2x-y2 x D.(x2 3x)-(2x 2)
15.在同一段路程里,上坡时的速度为a,下坡时的速度为b,则上、下坡的平均速度为
A. 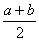 B.
B. 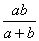 C.
C. 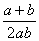 D.
D. 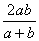
16.关于x的方程 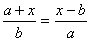 2(a≠b)的解为
2(a≠b)的解为
A.x=a-b B.x=a b C.x=2ab D.x=b-a
三、解答题(共52分)
17.(6分)当a= 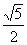 ,b=-
,b=- 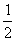 时,求代数式(a-b
时,求代数式(a-b 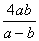 )·(a b-
)·(a b- 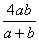 )的值.
)的值.
18.(6分)已知:如图(5),AB=4,BC=12,CD=13,DA=3,AB⊥AD.求证:BC⊥BD.
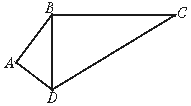
图(5)
19.(6分)已知钝角△ABC.
求作:BC边上的高AD和△A′B′C′,使△A′B′C′与△ABC关于AD所在直线对称.
图(6)
20.(6分)先化简,再求值: 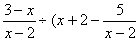 ),其中x=
),其中x= 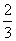 .
.
21.(7分)a为何值时,关于x的方程 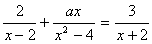 会产生增根?
会产生增根?
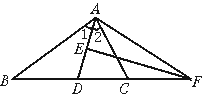
22.(7分)已知△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于F.
求证:∠BAF=∠ACF.
图(7)
23.(7分)AB两地相距80千米,一辆公共汽车从A地出发开往B地,2小时后又从A地同方向开出一辆小汽车,小汽车的速度是公共汽车的3倍,结果小汽车比公共汽车早40分钟到达B地,求两种汽车的速度.
24.(7分)观察下列等式:
9-1=8
16-4=12
25-9=16
36-16=20
………………
这些等式反映出自然数间的某种规律,设n表示自然数,用关于n的等式表示出来.
参考答案
一、1.9 25 2.- 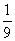 3.≠-
3.≠- 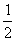 且x≠0 4.等边
且x≠0 4.等边
5. 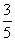 (∵
(∵ 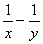 =3,∴x-y=-3xy,
=3,∴x-y=-3xy, 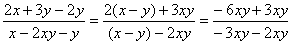
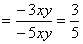 )
)
6. 6 1.5 7.3 正方形 4 8.2 cm<x<18 cm 25 cm
二、9.D 10.B 11.C 12.B 13.A 14.C 15.D 16.D
三、17.解:原式= 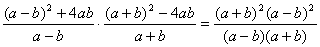 =a2-b2
=a2-b2
当a= 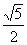 ,b=
,b= 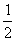 时,原式=(
时,原式=( 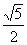 )2-(-
)2-(- 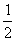 )2=
)2= 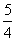 -
- 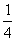 =1
=1
18.证实:∵AB⊥AD,∴∠BAD=90°
在Rt△ABD中,BD2=AB2 AD2=42 32=25
在△BCD中
∵BC2 BD2=122 25=169=132=CD2
∴∠DBC=90°∴BC⊥BD.
19.图略 作法
(1)过点A作BC的垂线交BC的延长线于D,则AD为BC边上的高
(2)分别作点B,点C,点A关于AD所在直线的对称点B′、C′与A′
(3)连结A′B′,A′C′,B′C′,△A′B′C′就是所要画图形
20.解:原式= 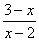 ÷(
÷( 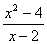 -
- 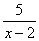 )=
)= 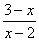 ×
× 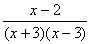 =-
=- 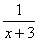
当x= 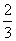 时,原式=-
时,原式=- 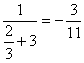 .
.
21.解:原方程可化为2(x 2) ax=3(x-2) (a-1)x=-10
此方程的增根x=±2
当x=2时,(a-1)×2=-10,a=-4
当x=-2时,(a-1)×(-2)=-10,a=6.
因此当a=-4或a=6时,关于x的方程 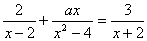 会产生增根.
会产生增根.
22.证实:∵AD是∠BAC的平分线,
∴∠1=∠2
∵FE是AD的垂直平分线
∴FA=FD,∠FAD=∠FDA
∵∠BAF=∠FAD ∠1,∠ACF=∠FDA ∠2
∴∠BAF=∠ACF.
23.解:设公共汽车的速度是x千米/小时,则小汽车的速度为3x千米/小时
根据题意得
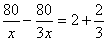
解之得x=20检验知x=20是方程的根,3x=3×20=60
答:公共汽车的速度是20千米/小时,小汽车的速度为60千米/小时.
24.(n 2)2-n2=4(n 1).
|