|
八年级(下)数学期末综合练习卷
测试时间90分钟 测试分值100分 学生姓名 实际评分
一、选择题(每小题3分,共30分)
1、为了了解某校初三年级400名学生的体重情况, 从中抽查了50名学生的体重进行统计分析, 在这个问题中, 总体是指( )
A. 400名学生 B. 被抽取的50名学生
C. 400名学生的体重 D. 被抽取的50名学生的体重
2、下列多项式中,不能用平方差公式分解的是( )
A.x2-y2 B.-x2-y2 C.4x2-y2 D.-4 x2
3、不等式 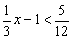 的正整数解有( )
的正整数解有( )
A.2个 B.3个 C.4个 D.5个
4、不等式组 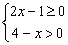 的解集为( )
的解集为( )
A. 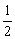 ≤x≤4 B.
≤x≤4 B. 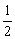 <x≤4 C.
<x≤4 C. 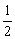 <x<4 D.
<x<4 D. 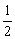 ≤x<4
≤x<4
 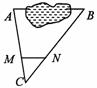 5、如图,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC分别取其三等分点M、N量得 MN=38m.则AB的长是 5、如图,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC分别取其三等分点M、N量得 MN=38m.则AB的长是
A. 152m B.114m C.76m D.104m
(第5题图) (第8题图)
6、下列各式从左到右的变形不正确的是( )
A. 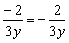 B
B 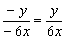 . C.
. C. 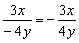 D.
D. 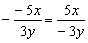
7、已知△ABC中,∠ABC与∠ACB的平分线交于O,则∠BOC一定( )
A.小于直角 B.等于直角 C.大于直角 D.大于或等于直角
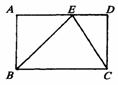
8、如图,在矩形ABCD中,点E是AD上任意一点,则有 ( )
A.△ABE的周长+△CDE的周长=△BCE的周长
B.△ABE的面积+△CDE的面积=△BCE的面积
C.△ABE∽△DEC
D.△ABE∽△EBC
9、化简 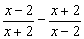 的结果是( )
的结果是( )
A. 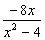 B.
B. 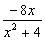 C.
C. 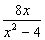 D.
D. 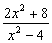
10、观察图形,判定 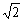 (a b)与2
(a b)与2 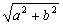 的大小( )
的大小( )
A. 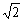 (a b)>2
(a b)>2 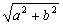 B.
B. 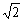 (a b)<2
(a b)<2 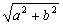
C. 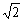 (a b)≤2
(a b)≤2 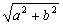 D.
D. 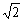 (a b)≥2
(a b)≥2 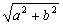
二、填空题(每小题3分,共24分)
11、分解因式: 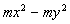 =
=
12、化简: 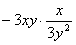 =
=
13、如图,CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠ACE=80°,则∠CAE= 度.
(第10题图) (第13题图) (第15题图)
14、已知关于x的不等式组 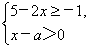 无解,则a的取值范围是________.
无解,则a的取值范围是________.
15、如图,在等边三角形ABC中,点D、E分别在AB、AC边上,且DE∥BC.假如BC=8 cm,AD∶AB=1∶4,那么△ADE的周长等于________ cm.
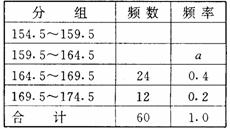 16、为了让学生适应体育测试中新的要求 16、为了让学生适应体育测试中新的要求
某学校抽查了部分初二男生的身高(注:身
高取整数).经过整理和分析,估计出该校
初二男生中身高在160cm以上(包括160cm)
的约占80%.右边为整理和分析时制成的
频率分布表,其中a= 。
17、某次数学测验满分为100(单位:分),某班的平均成绩为75,方差为10.若把每位同学的成绩按满分120进行换算,则换算后的平均成绩与方差分别是 .
18、在一次“人与自然”知识竞赛中,竞赛试题共有25道题.每道题都给出4个答案,其中只有一个答案正确.要求学生把正确答案选出来.每道题选对得4分,不选或选错倒扣2分.假如一个学生在本次竞赛中的得分不低于60分,那么,他至少选对了___________道题.
三、解答题(每小题6分,共18分)
19、求不等式组 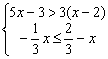 的整数解。
的整数解。
20、计算: 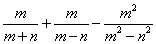
21、解方程: 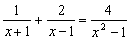
四、(每小题6分,共12分)
22、有若干个舞蹈演员在舞台上排成一排跳舞,面对观众作队形排列变化,其变化规律是:
一个舞蹈演员A1跳舞,面对观众作队形排列变化的种数是A1为1种;
二个舞蹈演员A1、A2跳舞,面对观众作队形排列变化的种数是A1A2 ;A2A1为2种即1×2种;
三个舞蹈演员A1、A2、A3跳舞,面对观众作队形排列变化的种数是A1A2A3 ,A1 A3A2 ;A2A1A3 ,A2 A3 A1;A3A1A2 ,A3 A2A1为6种即1×2×3种;
请你推测:
(1) 四个舞蹈演员A1、A2、A3、A4跳舞,面对观众作队形排列变化的种数是__ 种;
(2)六个舞蹈演员跳舞,按上述方法作队形排列变化的种数为(用科学记数法表示)_____ 种;
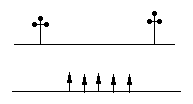 23、条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽. 23、条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.
五、(每小题8分,共16分)
24、根据卫生部2003年对5月21日至5月26日我国内地非典型肺炎疫情的通报,整理列表如下:(单位:人)
阅读图表,根据要求回答下列问题:
(1)出院累计人数和现有在院治疗人数这两组
数据说明了什么问题?
(2)请把表中天天的病例累计人数在下图中用
点描出并用折线顺次连结,从中你得到什么结论?
(3)从表中可以看出:今日病例累计=昨日病
例累计+今日新增病例-今日排除病例.请仿照
归纳今日现有疑似合计分别与表中哪几项有关?
并用公式的形式写出,然后加以验证.
25、烟台大樱桃闻名全国,今年又喜获丰收,某大型超市从大樱桃生产基地购进一批大樱桃,运输过程中质量损失5%.(超市不负责其它费用)
(1)假如超市把售价在进价的基础上提高5%,超市是否亏本?通过计算说明.
(2)假如超市要获得至少20%的利润,那么大樱桃售价最低应提高百分之几?(结果精确到0.1%)
参考答案:
一、CBCDD DCBAC
二、11、m(x-y)(x y) 12、 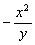 13、50 14、a≥3 15、6 16、0.2
13、50 14、a≥3 15、6 16、0.2
17、90 14.4 18、19
三、19、不等式的整数解为-1,0,1 20、 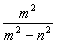 21、原方程无解
21、原方程无解
四、22、(1)1×2×3×4=24 (2)1×2×3×4×5×6=7.2×102 23、37.5m
五、24、(1)出院累计人数越来越多,现有在院治疗人数越来越少,说明治愈的非典病人大幅度增加,从而说明我们治愈非典的能力越来越强。
(2)折线图略。从图表可以看出,5月21日至5月25日,病例累计人数逐渐增加,5月25日至5月26日没有增加,说明疫情得到了更加有效的控制,也说明了我们治疗非典的经验越来越丰富,人们的防范意识越来越强。
(3)今日现有疑似合计与昨日现有疑似合计、今日新增疑似、今日排除疑似、今日其中疑似转来有关。
公式为:今日现有疑似合计=昨日现有疑似合计 今日新增疑似-今日排除疑似-今日其中疑似转来。
如:5月26日现有疑似合计1510=1573 29-85-7
25、设超市购进大樱桃a千克,进价为b元/千克,则购进这批大樱桃的成本费用为ab元,销售金额为(1-5%)a·(1 5%)b=(1-5%)(1 5%)ab元
(1)∵(1-5%)(1 5%)<1,∵ (1-5%)(1 5%)ab<ab,故超市亏本了。
(2)设超市售价为x %,超市才能获得至少20%的利润,由题意,得
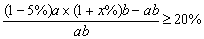 ,即(1-5%)(1 x%)-1≥20%
,即(1-5%)(1 x%)-1≥20%
解得x≥ 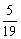 ,即x≥26.3%
,即x≥26.3%
答:略
|