|
一、填空(3分×10=30分)
1、假如△ABC≌△DEF,△DEF周长是32cm,DE=9cm,EF=13cm.∠E=∠B,则AC=________。
2、如图,某人把一块三角形的玻璃打坏成了三块,现在你要到玻璃店去配一块完全一样的玻璃,则应带哪块玻璃去__________(填上玻璃序号)。
3、已知△ABC中,∠BAC=60°,将△ABC绕着点A顺时针旋转40°,如图所示,则△BAC′的度数为______。
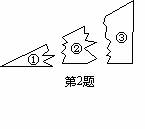 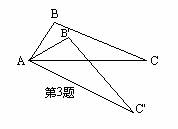 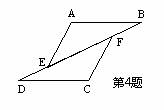
4、如图,点D、E、F、B在同一直线上,AB∥CD、AE∥CF,且AE=CF,若BD=10,BF=2,则EF=____________。
5、△ABC中,AC=4,中线AD=6,则AB边的取值范围是______________。
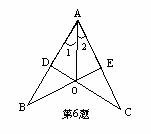
6、已知如图,CD⊥AB,BE⊥AC,垂足分别为D、E、BE、CD相交于O点,∠1=∠2,图中全等的三角形共有________对。
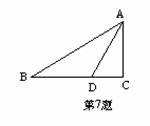
7、如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=10cm,BD=6cm,则点D到AB的距离为_________。
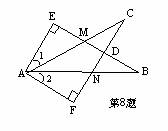
8、如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论是________(填序号)。
   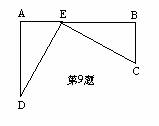 
9、如图,已知铁路上A、B两站(视为线上两点)相距45km,C、D为铁路同旁的两个村庄(视为两点),DA⊥AB于A,CB⊥AB于B,DA=25km,CB=20km,现在要在铁路AB上建一个收购站E,使C、D两村庄到E站的距离相等,则E站应建在距A站_______km处。
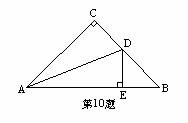
10、如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,
交BD于D,DE⊥AB于E,且AB=10,则△DEB周长为_______。
二、选择题(3分×10=30分)
11、如图△ABC≌△BAD,点A和点B,点C和点D是对应点,
若AB=6cm,BD=5cm,AD=4cm,则BC长为( )
A、4cm B、5cm C、6cm D、无法确定
12、如图△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,
∠AEC=120°,则∠DAC的度数等于( ) 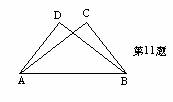 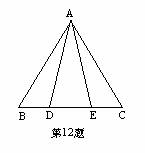
A、120° B、70° C、60° D、50°
13、在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,
在下面判定中错误的是( )
A、若添加条件AC=A′C′,则△ABC≌△A′B′C′
B、若添加条件BC=B′C′,则△ABC≌△A′B′C′
C、若添加条件∠B=∠B′,则△ABC≌△A′B′C′
D、若添加条件∠C=∠C′,则△ABC≌△A′B′C′
14、工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是( )
A、SSS B、SAS C、ASA D、HL 
15、下列命题错误的是( )
A、全等三角形的对应线段相等 B、全等三角形的面积相等
C、一个锐角和相邻的直角边对应相等的两个直角三角形全等
D、两角对应相等的两个三角形全等
16、不能确定两三角形全等的条件是( )
A、三条边对应相等 B、两条边及其夹角对应相等
C、两角和一条边对应相等 D、两条边和一条边所对应的角对应相等
17、在△ABC和△A′B′C′中,①AB=A′B′;②BC=B′C′;③AC=A′C′;④∠A=∠A′;⑤∠B=∠B′;⑥∠C=∠C′,则下列哪组条件不能保证△ABC≌△A′B′C′( )
A、①②③ B、①②⑤ C、①⑤⑥ D、①②④
18、如图△ABC中,∠C=90°,AB=2BC,D为AB中点过点D作DE⊥AB交AC于点E,下列结论:①CE=DE;②AE=BC;③∠B=2∠A;④∠A=30°中正确个数为( )
A、1个 B、2个 C、3个 D、4个
19、如图,在△ABC中,AB=AC,BF=CD,BD=CE,∠FDE=α ,则下列结论正确的是( )
A、2 α ∠A=180° B、α ∠A=90°
C、2α ∠A=90° D、 α ∠A=180° 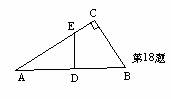 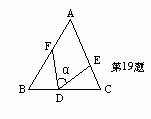 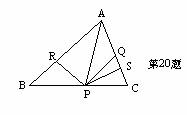
20、如图,已知△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,RS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP( )
A、全部正确 B、仅①和②正确
C、仅①正确 D、仅①和③正确
三、解答题
21、已知:△DEF≌△MNP,且EF=NP,∠F=∠P,∠D=58°,∠E=62°,MN=10cm,求∠P的度数及DE的长。(5分)
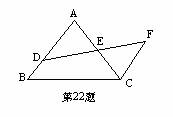
22、如图,D是AB上一点,DF交AC于点E,AE=CE,FC∥AB,求证:DE=EF。(5分)
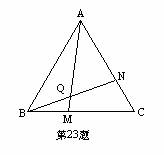
23、如图,△ABC为等边三角形,点M、N,分别在BC、AC上,且BM=CN,AM与BN交于Q点,求∠AQN的度数。(6分)
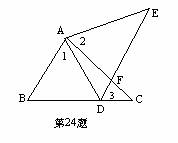
24、如图,点E在△ABC的外部,点D在BC边上,DE交AC于点F,若∠1=∠2 =∠3,AC=AE,求证:AB=AD。(6分)
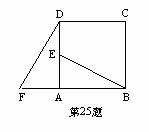
25、如图,在正方形ABCD中,E是AD中点,F是BA延长线上一点,AF= AB,则线段BE与DF大小,位置有什么关系?并证实你的结论。(7分)
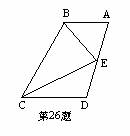
26、如图,AB∥CD,BE平分∠ABC,点E为AD中点,且BC=AB CD,求证:CE平分∠BCD。(7分)
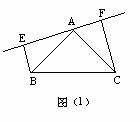
27、如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F。
(1)如图,①过A的直线与斜边BC不相交时,求证:EF=BE CF(4分)
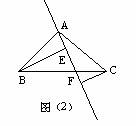
(2)如图,②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,试求:FE长。(4分)
28、在直角坐标系xOy中,O为坐标原点直线AB平行直线:y = x,且与x轴交于点A(-3,0),与y轴交于B点,点M、N在x轴上,(点M在点N的左边),点N在原点的右边作MP⊥BN,垂足为P(点P在线段BN上,且点P与点B不重合)直线MP与y轴交于点G,MG=BN。
(1)求直线AB的解析式及B点坐标;(4分)
(2)求点M的坐标;(4分)
(3)设ON=t,△MOG的面积为S,求S与t的函数关系式,并写出自变量t的取值范围;(4分)
(4)若以A为锐角顶点,直角顶点D在x轴上的直角三角形ADF与以A、O、B为顶点的直角三角形全等,设F(a、b),求a、b值(只需写出结果,不必写出解答过程)。(4分)
|