|
数学试卷
(人教版)
一、选择题:(每题3分,共30分)
1.如图,射线l甲、l乙分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的函数关系,则他们的行进的速度关系是( )
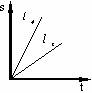
A.甲比乙快 B.乙比甲快 C.甲、乙同速 D.不一定
2.若直线l与直线y=2x+1关于y轴对称,则直线l的解析式为( )
A.y=-2x-1 B.y=-2x+1 C.y=2x-1 D.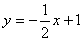
3.代数式a+bc,3x,ax²,ax²+bx+c,8,abc,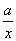 , ,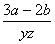 中有( ) 中有( )
A.7个整式 B.4个单项式,2个多项式
C.8个整式 D.5个单项式,3个多项式
4.如图,AB∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF∥BC于F,那么图中全等的三角形有( )对
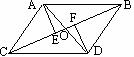
A.5 B.6 C.7 D.8
5.下列图形不是轴对称图形的是( )
A.等边三角形 B.线段 C.任意三角形 D.等腰三角形
6.若A=3m²-5m+2,B=3m²-4m+2,则A与B的关系是( )
A.A<B B.A>B C.A=B D.以上都有可能
7.如图,用整个圆表示某班的总人数,那么表示该班人数35%的扇形为( )
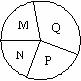
A.M B.N C.P D.Q
8.在△ABC中,AC=5,中线AD=4,那么边AB的取值范围为( )
A.1<AB<9 B.3<AB<13 C.5<AB<13 D.9<AB<13
9.已知多项式ax²+bx+c因式分解的结果为(x-1)(x+4),则abc为( )
A.12 B.9 C.-9 D.-12
10.在频数分布直方图中,各小长方形的底等于相应各组的( )
 A.组距 B.频数 C.频率 D.样本个体 A.组距 B.频数 C.频率 D.样本个体
二、填空题:(每空3分,共24分)
11.写一个系数为-3,含有字母x、y的四次单项式_____________。
12.如果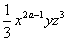 与 与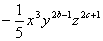 的和的系数为 的和的系数为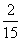 ,则a-2x+c=_____________。 ,则a-2x+c=_____________。
13.若x=2m+1,y=3+4m,用x的代数式表示y为_____________。
14.如图,AD,A′D′分别是锐角△ABC和△A′B′C′中BC.B′C′边上的高,且AB=A′B′,AD=A′D′,若使△ABC≌△A′B′C′,请你补充一个条件_____________。
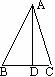 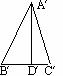
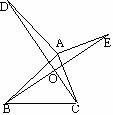
15.如图,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,则∠DOE=____________。
16.已知多项式mx5+nx3+px-4,当x=2时,此多项式的值为5,则当x=-2时,多项式值为_____________。
17.如果等腰三角形的腰长不变,而顶角逐渐变大,那么底边的长度逐渐_____________ ,三角形的面积先逐渐_____________,再逐渐_____________。
18.一个等腰三角形的周长为14cm,且一边长为4cm,则腰长为_____________。
三、计算:(每小题5分,共20分)
19.(1)化简:2x-{-3y+[4x-(3x-y)]};
(2)已知2x-y=10,求[(x²+y²)-(x-y)²+2y(x-y)]÷4y的值;
(3)已知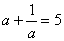 ,求 ,求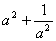 ; ;
(4)分解因式:x²-y²-z²-2yz。
四、解答题:(每小题8分,其中24题14分,共46分)
20.某中学举行了一次演讲比赛,分段统计参赛同学的成绩,结果如下表所示:
|
分数段(分) |
61~70 |
71~80 |
81~90 |
91~100 |
|
人数(人) |
2 |
8 |
6 |
4 |
据表将其制作成频数分布直方图。
21.已知m²-mn=15,mn-n²=-6,求3m²-mn-2n²的值。
22. 某厂日产笔盒的总成本y(元)与笔盒日产量x(个)之间的关系是y=3x+4000,笔盒的出产价格为每个5元,问该厂笔盒日产量至少多少个才不亏本?
四、用心想一想:(共36分)
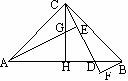
23.如图,在等腰Rt△ABC中,∠C=90°,D是斜边AB上任意一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H,交AE于G,求证:BD=CG。
24.在平面直角坐标系中,已知点A(4,0),点P是第一象限内直线x+y=6上的点,O为坐标原点。
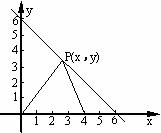
(1)已知P(x,y),求△OPA 的面积s与x的函数关系式;
(2)当s=10时,求P点坐标;
(3)在x+y=6上求一点P,使△OPA是以OA为底的等腰三角形。
2006年云台中学八年级上学期期末测试
数学试卷
参考答案
一、选择题
1. A
2. B
3. B
4. C
5. D
6. C
7. D
8. B
9. D
10. A
二、填空题
11.略
12.1
13.y=x²-2x+4
14.略
15.90°
16.-13
17.增大,增大,变小
18.5cm或4cm。
三、计算题
19.(1) x+2y
(2)由已知条件得: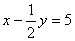 ,∴原式= ,∴原式=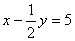
(3) 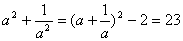
(4)原式=x²-(y+z)²=(x+y+z)(x-y-z)。
20.略
21.由已知条件可得: m²-n²=9。
∴ 原式=2(m²-n²)+m²-mn=18+15=33。
22.根据题意,当该厂日产总成本不少于3x+4000时不亏本,
∴ 5x≥3x+4000,x≥2000,即该厂日产量至少2000个才不亏本。
23.先证△AEC≌△CFB,
∴ CE=FB。再证△CEG≌△BFD,∴ CG=BD。
24.(1)如图,显然△OPA的面积为4y,再将直线解析式y=6-x代入其中,
得:S=-2x+12
(2)将S=10代入(1)中面积关系得:x=1
再将x=1代入直线解析式得:y=5。故得P点坐标为:P(1,5)
(3)当顶点P的横坐标为2时,△OPA是以OA为底边的等腰三角形,此时,y=4,故得P(2,4)。
|