|
华师大2006年八年级下期末测试试卷
(90分钟完卷,满分100分)
班级 姓名 学号
一、选择题(每题3分,共30分)
1.9的的算术平方根是( )
A.81 B.3 C.-3 D.±3
2.反比例函数 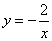 的图象的两个分支分别位于( ) 的图象的两个分支分别位于( )
A.第一、三象限 B.第一、四象限 C.第二、四象限 D.第二、三象限
3.若直角三角形的两边分别是2和3,则第三边是( )
A. 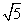 B.4 C. B.4 C. 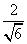 D.
D. 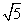 或
或 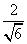
4.下列二次根式中,与 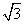 是同类二次根式的是( )
是同类二次根式的是( )
A. 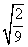 B.
B. 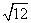 C.
C. 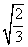 D.
D. 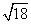
5.若两个相似三角形的周长分别为80cm和140cm,这两个相似三角形的相似比是( )
A.2∶3 B.4∶7 C.3∶2 D.7∶4
6.在一个口袋里有5个红球,5个白球,任意摸一个,则( )
A.只能摸到一个红球 B.只能摸到一个白球
C.可能摸到白球 D.不可能摸到红球
7.在△ABC中,∠C=90°,假如cotA= 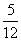 ,那么cosB=( ) ,那么cosB=( )
 A. A.  B.
B. 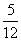 C.
C.  D.
D. 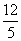
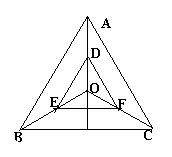
8.如图,点O是等边△ABC的中心,D、E、F分别是OA、
OB、OC的中点,则△DEF与△ABC是位似三角形,此时△DEF
与△ABC的位似比,位似中心分别为( )
A.2、点B B. 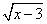 、点B
、点B
C.2、点O D. 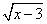 、点O
、点O
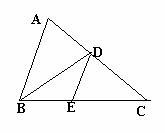 9.如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC 9.如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC
于E,EC=3,BE=2,则AB=( )
A.4 B.6 C. 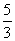 D.
D. 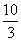
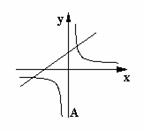
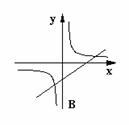
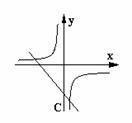
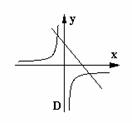
10.函数 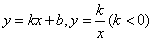 ,它们在同一坐标系中的大致图象是( )
,它们在同一坐标系中的大致图象是( )
二、填空:(每题3分,共24分)
11.化简: 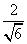 = 。
= 。
12.当x 时, 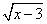 有意义。
有意义。
13.计算: 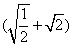 ·
· 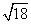 =
=
14.正比例函数y=kx的图象经过点(-1,-2),则k= 。
15.在△ABC中,∠C=90°,c=6,a=4,则sinA= ,cotB= 。
 16.将函数y=2x的图象向下平移3个单位,则平移后的直线所对应的函数关系是 16.将函数y=2x的图象向下平移3个单位,则平移后的直线所对应的函数关系是
17.如图,点D、E分别在△ABC的边AC、AB上,要使△ABD∽△ACE,
已具备了一个条件 ,还需添加一个条件 。
 18.如图,AC∥BD∥EF,AC=20, 18.如图,AC∥BD∥EF,AC=20,
BD=80,则EF= 。
三、计算:(每题4分,共8分)
19. 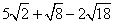 20.
20. 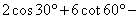 2tan245°
2tan245°
四、解下列各题(每题5分,共15分)
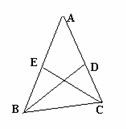
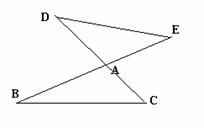 21.已知:如图,BE与CD交于点A,∠B=∠D, 21.已知:如图,BE与CD交于点A,∠B=∠D,
试说明AB·DE=AD·BC
22.某单位要从技术优秀的甲、乙两名车工中选拔一名参加直径为10毫米的零件加工技术比赛,随机抽取甲、乙两名车工加工5个零件,测得结果如下表:
|
甲 |
9.96 |
10.05 |
9.97 |
10.02 |
10 |
|
乙 |
10.02 |
10 |
10.01 |
10 |
9.97 |
⑴分别求以上两组数据的方差(精确到0.001);⑵你建议选谁参赛。
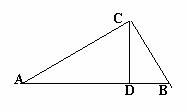 23.如图,在△ABC中,CD⊥AB,∠A=30°,CD=3, 23.如图,在△ABC中,CD⊥AB,∠A=30°,CD=3,
BC=2 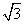 ,求AB的长。
,求AB的长。
 五、(第33题7分,第34题8分,共15分) 五、(第33题7分,第34题8分,共15分)
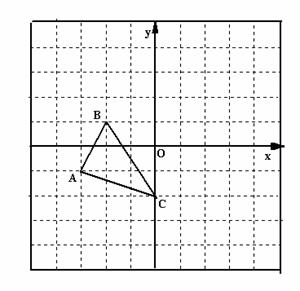
24.将图中的△ABC作下列运动,
画出相应的图形
⑴沿y轴向下平移3 个单位;
⑵关于y轴对称;
⑶以点A为位似中心,放大到2倍得
到△AB’C’,并写出A、B’、C’三点
的坐标。
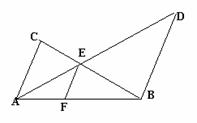
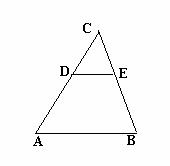 25.如图,在△ABC中,假如DE∥AB,BE=5,CE=4,CD=3。 25.如图,在△ABC中,假如DE∥AB,BE=5,CE=4,CD=3。
⑴说明△DEC∽△ABC;
⑵求 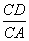 的值;
的值;
⑶求AC和AD的值;
⑷若△CDE的面积为8cm2,求四边形ABED的面积。
 六、(本题8分) 六、(本题8分)
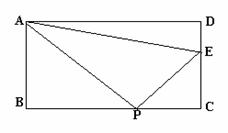
26.如图:矩形ABCD中,BC=12 cm,CD=6 cm,
点P沿CB边从点C开始向点B以每秒2 cm的速度
移动,点E沿DC边从点D开始向点C以每秒1 cm
的速度移动,假如P、E同时出发,用t表示移动的
时间(0≤t≤6),那么:
⑴当t为何值时,△CPE为等腰三角形;
⑵当t为何值时,以C、P、E为顶点的三角形与△BAC相似。
2006年八年级下数学期末测试试卷参考答案及评分意见
一、⒈B ⒉C ⒊D ⒋C ⒌D ⒍B ⒎B ⒏C ⒐A ⒑D ⒒D ⒓C
二、⒔0.7,/3 ⒕x≥3 ⒖9 ⒗1.7690 ⒘2 ⒙2 ⒚ 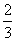 , ⒛10,11.5 21、y= 2x-3 22、∠A=∠A、∠ADB=∠AEC或
, ⒛10,11.5 21、y= 2x-3 22、∠A=∠A、∠ADB=∠AEC或 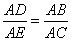 23、y=20-2x,5<x<20 24、16.
23、y=20-2x,5<x<20 24、16.
三、25、解:原式=5 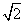 2
2 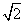 - 6
- 6 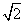 (3分) =
(3分) = 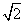 (5分)
(5分)
26、解:原式=( 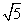 )2-(2
)2-(2 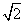 )2(2分)= 5-8(4分)= -3 (5分)
)2(2分)= 5-8(4分)= -3 (5分)
27、解:原式= 2- 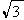 - - 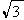 -1(3分)=1-2 -1(3分)=1-2 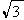 (5分) (5分)
28、解:原式=2× 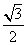 6×
6× 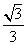 -2×12 (3分)=
-2×12 (3分)= 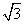 2
2 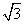 -2 (4分)
-2 (4分)
=3 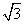 -2 (5分)
-2 (5分)
四、1、解:⑴由己知得 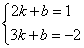 (1分) 解之得
(1分) 解之得 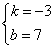 (2分)
(2分)
∴所求的函数解析式是y=-3x 7(3分)
⑵过点(0,7),(7/3,0)得直线y= -3x 7,图略 (5分)
30、解:∵∠B= ∠D,∠BAC=∠DAE(1分) ∴△ABC∽△ADE(3分)
∴ 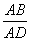
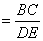 (4分)∴AB·DE= AD·BC(5分)
(4分)∴AB·DE= AD·BC(5分)
31、解:⑴S甲≈0.033(毫米)(2分)S乙≈0.017(毫米)(4分)
⑵∵S甲>S乙(5分)∴ 建议选乙参赛
32、解:在△ACD中,∠A=30°,CD= 3。∴cot∠A= 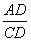
∴AD= CD·cotA= 3× 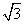 =3
=3 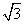 (2分)
(2分)
在△BCD中 ,BD2 =BC2-CD2 ∴BD2 =(2 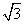 )2-32 = 12-9 = 3(4分)
)2-32 = 12-9 = 3(4分)
∴BD = 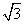 ∴AB=AD BD= 3
∴AB=AD BD= 3 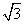
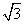 =4
=4 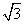 (5分)
(5分)
五、33、解:⑴略 ⑵略 ⑶A(-3,-1)、B(-1,3)、C(3,-3)
34、解:⑴∵DE∥AB ∴∠CDE=∠A(1分) ∵∠C=∠C
∴△DEC∽△ABC(2分)
⑵∵△DEC∽△ABC,BC= 5 4 = 9(3分) 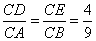 (4分)
(4分)
⑶AC= 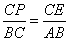 ,AD=
,AD= 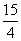 (6分)
(6分)
⑷∵△DEC∽△ABC ∴S△DEC∶S△ABC =( 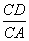 )2 ∴8/ S△ABC =
)2 ∴8/ S△ABC = 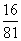
∴S△ABC = 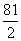 (7分) ∴S四边形ABDE =
(7分) ∴S四边形ABDE = 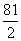 -8=
-8= 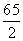 (cm2 )(8分)
(cm2 )(8分)
六、解:⑴∵CP=2t ,CE= 6-t ∴2t = 6-t (1分) ∴t = 2
∴当t = 2秒时,△CPE为等腰三角形 (2分)
⑵若 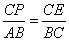 ∵
∵ 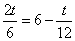 ∴t = 1.2(秒)(4分)
∴t = 1.2(秒)(4分)
若 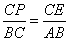 ∵
∵ 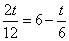 ∴t= 3(秒)(5分)
∴t= 3(秒)(5分)
∴当t 等于1.2或3秒时,△CPE与△BAC相似
|