|
八年级下期数学期中测试
数 学
一.选择题(每小题3分,共30分)
1.0.00248用科学记数法表示为( )
 A. 2.48×10-3 B.2.48×10-4 C. 0.248 LINK Word.Document.8 E:\\shijuan\\八年级下期期中测试.doc OLE_LINK2 \a \r \* MERGEFORMAT 。 D. LINK Word.Document.8 F:\\shiti\\八年级下期数学期中测试.doc OLE_LINK3 \a \r \* MERGEFORMAT 错误!链接无效。-4 A. 2.48×10-3 B.2.48×10-4 C. 0.248 LINK Word.Document.8 E:\\shijuan\\八年级下期期中测试.doc OLE_LINK2 \a \r \* MERGEFORMAT 。 D. LINK Word.Document.8 F:\\shiti\\八年级下期数学期中测试.doc OLE_LINK3 \a \r \* MERGEFORMAT 错误!链接无效。-4
2.下列说法正确的是( )
A.分式的分子中一定含有字母 B.当B = 0时,分式 无意义
 C.当A=0时,分式 的值为0(A、B为整式) D.分数一定是分式 C.当A=0时,分式 的值为0(A、B为整式) D.分数一定是分式
3.若 的值为0,则x的值为( )
A、1 B、-1 C、1或-1 D、0
4.点M(1,2)关于x轴对称点的坐标为( )
A、(-1,2) B、(-1,-2) C、(1,-2) D、(2,-1)
5. 一次函数y=-2x 3的图像不经过的象限是( ).
A 第一象限 B 第二象限 C 第三象限 D 第四象限
6.一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走了一段路程,爸爸才开始出发.图中 \* MERGEFORMAT 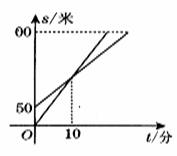 两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t(分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( ) 两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t(分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( )
A.爸爸登山时,小军已走了50米
B.爸爸走了5分钟,小军仍在爸爸的前面
C.小军比爸爸晚到山顶
D.爸爸前10分钟登山的速度比小军慢,10分钟后登山的速度比小军快
7、假如反比例函数 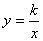 \* MERGEFORMAT
的图像经过点(-3,-4),那么函数的图像应在( )
\* MERGEFORMAT
的图像经过点(-3,-4),那么函数的图像应在( )
A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限
8、若反比例函数 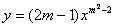 \* MERGEFORMAT
的图像在第二、四象限,则
\* MERGEFORMAT
的图像在第二、四象限,则 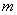 \* MERGEFORMAT
的值是( )
\* MERGEFORMAT
的值是( )
A、-1或1 B、小于 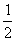 \* MERGEFORMAT
的任意实数 C、-1 D、不能确定
\* MERGEFORMAT
的任意实数 C、-1 D、不能确定
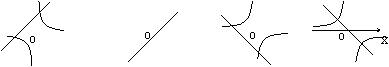
 9、正比例函数
9、正比例函数 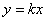 \* MERGEFORMAT
- k例函数在同一坐标系内的图象为( )
\* MERGEFORMAT
- k例函数在同一坐标系内的图象为( )
A B C D
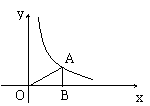 10、如右图,A为反比例函数 10、如右图,A为反比例函数 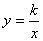 \* MERGEFORMAT
图象上一点,AB垂直
\* MERGEFORMAT
图象上一点,AB垂直 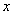 \* MERGEFORMAT
轴于B点,
\* MERGEFORMAT
轴于B点,
若S△AOB=3,则 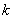 \* MERGEFORMAT
的值为( )
\* MERGEFORMAT
的值为( )
A、6 B、3 C、 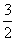 \* MERGEFORMAT
D、不能确定
\* MERGEFORMAT
D、不能确定
二.填空题(每小题3分,共30分)
11、( 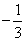 )0× 3-1=
)0× 3-1=
12、当x 时,分式 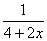 有意义。
有意义。
13、函数y = 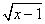 中,自变量x 取值范围是 。
中,自变量x 取值范围是 。
14、一次函数  \* MERGEFORMAT
的图象经过点P(-1,2),则
\* MERGEFORMAT
的图象经过点P(-1,2),则  \* MERGEFORMAT
.
\* MERGEFORMAT
.
15、若函数 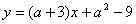 \* MERGEFORMAT
是正比例函数,则
\* MERGEFORMAT
是正比例函数,则  \* MERGEFORMAT
\* MERGEFORMAT
16、直线 y =3x 2与直线y = -3x 4的交点坐标是
17、 直线 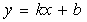 \* MERGEFORMAT
与
\* MERGEFORMAT
与 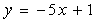 \* MERGEFORMAT
平行,且经过(2,1),则b = .
\* MERGEFORMAT
平行,且经过(2,1),则b = .
18、已知变量 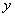 \* MERGEFORMAT
与
\* MERGEFORMAT
与 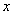 \* MERGEFORMAT
成反比例,当
\* MERGEFORMAT
成反比例,当 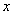 \* MERGEFORMAT
=3时,
\* MERGEFORMAT
=3时, 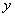 \* MERGEFORMAT
=―6;那么当
\* MERGEFORMAT
=―6;那么当 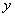 \* MERGEFORMAT
=3时,
\* MERGEFORMAT
=3时, 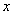 \* MERGEFORMAT
的值是
\* MERGEFORMAT
的值是
19、某书定价 8 元,假如购买 10本以上,超过 10 本的部分打八折。请写出购买数量
x(本)(x>10) 与付款金额 y(元)之间的关系式___________________。
20、已知 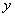 \* MERGEFORMAT
-2与
\* MERGEFORMAT
-2与 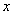 \* MERGEFORMAT
成反比例,当
\* MERGEFORMAT
成反比例,当 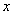 \* MERGEFORMAT
=3时,
\* MERGEFORMAT
=3时, 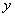 \* MERGEFORMAT
=1,则
\* MERGEFORMAT
=1,则 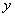 \* MERGEFORMAT
与
\* MERGEFORMAT
与 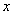 \* MERGEFORMAT
间的函数关系式为 ;
\* MERGEFORMAT
间的函数关系式为 ;
三.解答题(共60分)
21、计算: 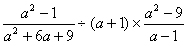 22、化简求值:
22、化简求值: 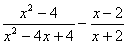 其中x =
其中x = 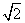 .
.
23、解方程: 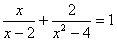
24、(10分)已知一次函数的图象经过点A(—2,—3),点B(1,3)两点。
(1)求这个一次函数的关系式 ;
(2)试判定点P(—1,1)是否在这个函数的图象上。
25、30、应用题:从甲地到乙地的路程是15千米,A骑自行车从甲地到乙地先走,40分钟后,B骑自行车从甲地出发,结果同时到达。已知B的速度是A的速度的3倍,求两车的速度。
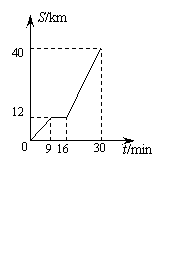
26、(10分)右图是某汽车行驶的路程S(km)与时间t(min)的 函 数关系图.
观察图中所提供的信息,解答下列问题:
 (1)汽车在前9分钟内的平均速度是多少? (1)汽车在前9分钟内的平均速度是多少?
(2)汽车在中途停了多长时间?
(3)当16≤t ≤30时,求S与t的函数关系式.
27、(10分)如图,正方形ABCD的边长为4,P为CD边上一点(与点D不重合)。设DP= 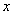 \* MERGEFORMAT
,
\* MERGEFORMAT
,
(1)求 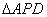 \* MERGEFORMAT
的面积
\* MERGEFORMAT
的面积 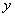 \* MERGEFORMAT
关于
\* MERGEFORMAT
关于 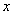 \* MERGEFORMAT
的函数关系式;
\* MERGEFORMAT
的函数关系式;
(2)写出函数自变量 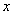 \* MERGEFORMAT
的取值范围;
\* MERGEFORMAT
的取值范围;
(3)画出这个函数的图象
\* MERGEFORMAT 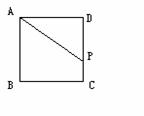
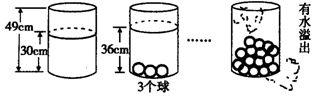
28.(10分)小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:
请根据图中给出的信息,解答下列问题:
(1)放入一个小球量筒中水面升高_______cm;
(2)求放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);
(3)量筒中至少放入几个小球时有水溢出?
|