|
(90分钟完成 满分100分)
一、填空题(每小题2分,共36分)
1.一次函数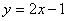 在y轴上的截距b = ,它与y轴的交点坐标是 。 在y轴上的截距b = ,它与y轴的交点坐标是 。
2.关于x的方程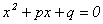 的根的判别式是 。 的根的判别式是 。
3.设方程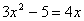 的两根为x1和x2,则x1+x2=________, 的两根为x1和x2,则x1+x2=________,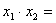 _______。 _______。
4.如果等腰三角形的底边上的高为4厘米,腰长为8厘米,那么底角的度数是 ,顶角的度数是 。
5.到已知角两边距离相等的点的轨迹是 。
6.如果直角三角形一条直角边为5,斜边上的中线长为6.5,那么另一条直角边长为 。
7.在Rt⊿ABC中,∠C=90°,∠A=30°,BC=2cm,则⊿ABC的周长为 。
8.如果平行四边形一组对角的和等于250°,那么其中较小的一个内角等于 。
9.矩形的两条对角线交角为120°,则对角线与较短边的比等于 。
10.某中学要在校园内划出一块面积是100m2的矩形土地做花圃,设这个矩形的相邻两边分别为xcm和ycm,那么y关于x的函数解析式是 。
11.矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为 cm2。
12.如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD= 。
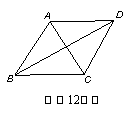
13.如图,梯形ABCD中,AB∥CD,E、F、G、H分别是边AB、BC、CD、DA的中点,梯形ABCD的边满足条件 时,四边形EFGH是菱形。
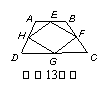
14.已知一个梯形的面积为10cm2,高为2cm,则该梯形的中位线的长度等于 cm。
15.正方形是轴对称图形,它的对称轴共有 条。
16.如果正方形的对角线长为2,则正方形的面积是 。
17.如果四边形的两条对角线相等,那么顺次连结四边形各边中点得到的四边形是 。
18.如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:
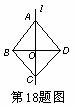
①AB∥CD;②AB=BC;③AB⊥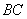 ;④AO=OC。 ;④AO=OC。
其中正确结论是 (把你认为正确结论的序号都填上)
二、选择题(每小题3分,共12分)
19.函数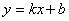 中,如果k>0,b<0,那么它的图象大致是( ) 中,如果k>0,b<0,那么它的图象大致是( )
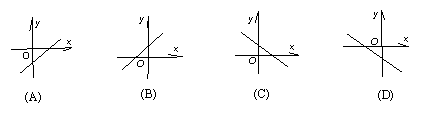
20.下列说法正确的是 ( )
A.函数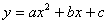 的图象一定是抛物线 的图象一定是抛物线
B.抛物线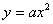 一定在x轴上方(顶点在x轴上) 一定在x轴上方(顶点在x轴上)
C.二次函数图象的对称轴是y轴
D.二次函数图象的顶点一定在其对称轴上
21.梯形的中位线长为15cm,一条对角线把中位线分成两段,两段之比为3:2,那么梯形上、下底的长为( )
A.18cm,12cm B.16cm,14cm
C.20cm,10cm D.22cm,10cm
22.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将⊿AED以DE为折痕向右折叠,AE与BC交于点F,则⊿CEF的面积为( )
A.4 B.6
C.8 D.10
三、解答题(每小题6分,共18分)
23.用配方法解方程: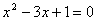
24.在⊿ABC中,∠C=90°,AC=12cm,BC=16cm。求:
(1)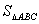 ; ;
(2)AB;
(3)AB边上的高。
25.在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,腰AB=8cm,求等腰梯形各角的度数和高。
四、解答题(每题8分,共24分)
26.把函数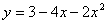 写成 写成 的形式,并写出函数图象的开口方向、顶点坐标和对称轴。 的形式,并写出函数图象的开口方向、顶点坐标和对称轴。
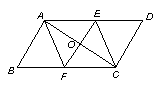
27.如图,在□ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F,求证:四边形AFCE是菱形。(推理过程可以不写理由)
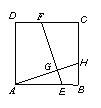
28.如图,在正方形ABCD中,H在BC上,EF⊥AH交AB于点E,交DC于点F.若AB=3,BH=1,求EF的长。
五、(满分10分)
29.如图,在平行四边形ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)
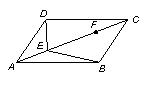
(1)连结 。
(2)猜想: = 。
(3)证明(要求每步写出理由):
2005年上海南汇区初二下学期期末测试
数学试卷
参考答案
一、填空题
1.-1、(0,-1)
2.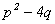
3.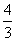 , ,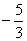
4.30°,120°
5.这个角的角平分线;
6.12
7.(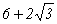 )cm )cm
8.55°
9.2:1
10.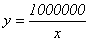
11.4或12
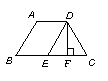
12.
13.AD=BC
14.5
15.4
16.2
17.菱形
18.①、②、④
二、选择题
19.A
20.D
21.A
22.C
三、解答题
23.解: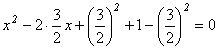 ……2分 ……2分
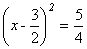 ……1分 ……1分
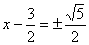 ……1分 ……1分
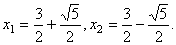 ……2分 ……2分
24.解:(1)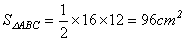 ……2分 ……2分
(2)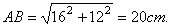 ……2分 ……2分
(3)设AB边上的高为x,则
20x=16×12,
x=9.6cm ……2分
25.解:过D作DE∥AB交BC于E,

则 DE=8cm,EC=14-6=8cm。 ……1分
所以⊿DEC为等边三角形 ……1分
所以 ∠B=∠C=60°,
∠A=∠ADC=120° ……2分
作DF⊥BC于F,F为垂足。
则 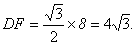 即梯形的高为 即梯形的高为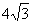 cm。 ……2分 cm。 ……2分
26.解: 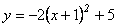 ……3分 ……3分
因为 2<0,所以开口向下。 ……1分
顶点坐标为(1,5) ……2分
对称轴方程为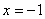 ……2分 ……2分
27.证明:如图,∵E、F分别是线段AC中垂线上的点,
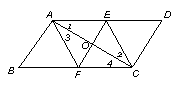
∴AE=EC,AF=FC
∴∠1=∠2,∠3=∠4 ……3分
又AE∥FC,∴∠1=∠4,∠3=∠2,
AF∥EC,所以四边形AFCE为平行四边形。 ……3分
又AE=EC,所以,□AFCE为菱形。 ……2分
28.解:作FM⊥AB于M,M为垂足

则FM=AB=3。 ……2分
∵∠1 +∠3=∠2 +∠3=90°
∴∠1 =∠2 ……2分
又FM=AB,所以 Rt⊿FME≌ Rt⊿ABH ……2分
∴ 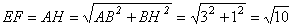 ……2分 ……2分
29.(1)DF ……2分
(2)DF、EB ……2分
(3)∵DC∥AB(平行四边形对边平行)
∴∠DCF=∠BAE(两直线平行,内错角相等) ……2分
又∵ DC=AB(平行四边形对边相等)
FC=AE(已知)
∠DCF=∠BAE(已证)
∴ ⊿DFC≌⊿BEA (SAS) ……2分
∴ DF=EB。 (全等三角形对应边相等) ……2分
(其他方法对应给分,第(3)小题没写理由扣3分)
|