|
班别 姓名 座号 成绩
一、填空题(每小题4分,共40分)
1、一直角三角形的斜边比直角边大 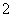 ,另一直角边为
,另一直角边为 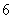 ,则斜边长为 。
,则斜边长为 。
2、当x 时,分式 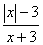 的值为0。
的值为0。
3、若等式成立,写出空白处的代数式: 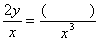
4、若四边形四个内角比为3∶4∶5∶6,则最小的内角是________.
5、若反比例函数 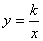 经过(-2,-1),则反比例函数解析式 。
经过(-2,-1),则反比例函数解析式 。
6、下列式子中:① 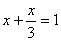 ;②
;② 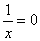 ;③
;③ 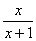 ;④
;④ 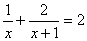 ;⑤
;⑤ 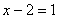 ;
;
⑥ 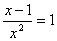 是分式方程的有 (填序号)。
是分式方程的有 (填序号)。
7、3、3、3、3、3的平均数是 ,方差是 .
8、如下图,已知OA=OB,那么数轴上点A所表示的数是_______。
9、平行四边形的周长是20 cm,相邻两边上的高分别为4 cm和 6 cm,则它的面积是________cm2.
10、假如x和y成正比例,y和z成正比例,那么x和z之间的关系式 .
二、选择题(每小题3分,共15分)
1、若线段a,b,c组成Rt△,则它们的比为( )
A、2∶3∶4 B、3∶4∶6 C、5∶12∶13 D、4∶6∶7
2、分式 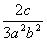 ,
, 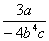 ,
, 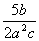 的最简公分母是 ( )
的最简公分母是 ( )
A、12a2b4c2 B、24a2b4c2 C、24a4b6c D、12a2b4c
3、某厂储存了t天用的煤m吨,要使储存的煤比预定的多用d天,那么天天应节约煤的吨数为( )
A、 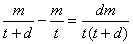 B、
B、 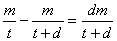
C、  D、
D、 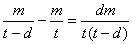
4、下列命题中,真命题是( )
A、四边相等的四边形是正方形 B、四角相等的四边形是正方形
C、对角线垂直的平行四边形是正方形 D、对角线相等的菱形是正方形
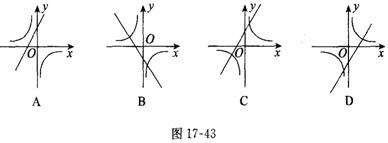
5、反比例函数 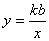 与一次函数 与一次函数 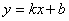 在同一坐标系中图象(图17—43)正确的是( ) 在同一坐标系中图象(图17—43)正确的是( )
三、解答题(每小题5分,共25分)
1、计算 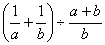 2、解方程
2、解方程 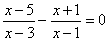
3、小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度。
4、已知,△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,试说明△ABC是等腰三角形。
5、已知:梯形ABCD中,AD∥BC,AB=DC,∠C=600,BD平分∠ABC,AD+BC=30cm,求AD和BC的长。

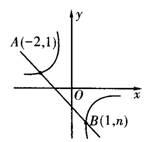
四、(6分)如图,一次函数y=kx b的图象与反比例函数 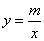 的图象交于A、B两点。
的图象交于A、B两点。
(1)根据图中条件,求反比例函数和一次函数的解析式;
(2) 根椐函数图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
 五、1、(6分)如图,四边形ABCD中,∠ABC=900,DE⊥BC于点E,DE交AF于点G,且 五、1、(6分)如图,四边形ABCD中,∠ABC=900,DE⊥BC于点E,DE交AF于点G,且
AF∥BC,BG∥AD。求证:EF=FC。
|
分组 |
频数 |
频率 |
|
1.565~1.595 |
2 |
0.04 |
|
1.595~1.625 |
4 |
0.08 |
|
1.625~1.655 |
6 |
0.12 |
|
1.655~1.685 |
11 |
0.22 |
|
1.685~1.715 |
17 |
0.34 |
|
1.715~1.745 |
6 |
0.12 |
|
1.745~1.775 |
4 |
0.08 |
|
合计 |
50 |
1 |
2、(8分) 为了了解学生的身高情况,抽测了某校17岁的50名学生的身高,数据如右表(单位:米)若将数据分成7组,取组距为0.03米,相应的频率分布如下表:
|
身高 |
1.57 |
1.58 |
1.59 |
1.60 |
1.61 |
1.62 |
1.63 |
1.64 |
1.65 |
1.66 |
1.68 |
1.69 |
1.70 |
1.71 |
1.72 |
1.73 |
1.74 |
1.75 |
1.76 |
1.77 |
|
人数 |
1 |
0 |
1 |
2 |
0 |
2 |
3 |
2 |
1 |
6 |
5 |
8 |
7 |
2 |
3 |
2 |
1 |
2 |
1 |
1 |
请回答下列问题:(1)样本数据中,17岁男生身高的众数,中位数分别是什么?
(2)依样本数据,估计这所学校17岁男生中,身高不低于1.65米且不高于1.70米的学生所占百分比;
(3)观察频率分布表,指出该校17岁的男生中,身高在哪个数据范围内频率最大,假如该校17岁男生共有350人,那么这个身高范围内的人数估计有多少人?
|