x

y＝2x

y＝2x＋3

解

2、3、说出直线y＝3x＋2与 ；y＝5x-1与y＝5x-4的相同之处．

解 :直线y＝3x＋2与 的 ，相同，所以这两条直线 ，同一点，且交点坐标 ，；直线y＝5x-1与y＝5x-4的 相同，所以这两条直线 ，．

4、（1）直线 和 的位置关系是 ，直线 可以看作是直线 向 平移 个单位得到的;; 向 平移 个单位得到的

(2)将直线y＝-2x＋3向下平移5个单位，得到直线 ．

(3).函数y＝kx-4的图象平行于直线y＝-2x，求函数若直线 的解析式为 ；

(4)直线y=2x-3可以由直线y=2x经过 单位而得到；直线y=-3x 2

可以由直线y=-3x经过 而得到；直线y=x 2可以由直线y=x-3经过

而得到．

（5）直线y=2x＋5与直线 ，都经过y轴上的同一点（ 、 ）

[B组]

5、写出一条与直线y=2x-3平行的直线

6、写出一条与直线y=2x-3平行，且经过点（2，7）的直线

7、直线y=－5x 7可以看作是由直线y=－5x－1向 平移 个单位得到的

第三课时（与坐标轴的交点）

[A组]

1、（1）一次函数y=kx b当x=0时，y= ，横坐标为0点在 上，在 中，；当y=0时，x= 纵坐标为0点在 上。。画一次函数的图象，常选取（0, ）、（ ,0）两点连线。（2）直线y＝4x－3过点（_____，0）、（0， ）；

（3）直线 过点（ ，0）、（0， ）．

2、 分别在同一直角坐标系内画出下列直线，写出各直线分别与x轴、y轴的交点坐标，并指出每一小题中两条直线的位置关系．

（1）y=－x 2 ； y=－x－1. （2）y=3x－2 ； y= .

3、直线y=－x 2与x轴的交点坐标是 ，与y轴的交点坐标是 　　

4、直线y=－x－1与x轴的交点坐标是 ，与y轴的交点坐标是 　　

5、直线y=4x－2与x轴的交点坐标是 ，与y轴的交点坐标是 　　

6、直线y= 与x轴的交点坐标是 ，与y轴的交点坐标是 　　

7、 画出函数y＝－2x＋3的图象，借助图象找出：

（1） 直线上横坐标是2的点，它的坐标是（ ， ）

（2） 线上纵坐标是－3的点，它的坐标是（ ， ）

（3） 直线上到y轴距离等于2的点，它的坐标是（ ， ）

（4）点（2、7）是否在此图象上；（ ）

（5）找出横坐标是-2的点，并标出其坐标；（ ， ）

（6）找出到 轴的距离等于1的点，并标出其坐标；（ ， ）

（7）找出图象与 轴和 轴的交点，并标出其坐标。（ ， ）

[B组]

9、求函数 与x轴、y轴的交点坐标，并求这条直线与两坐标轴围成的三角形的面积.

分析 求直线 与x轴、y轴的交点坐标，根据x轴、y轴上点的纵坐标和横坐标分别为0，可求出相应的横坐标和纵坐标；结合图象，易知直线 与x轴、y轴围成的三角形是直角三角形，两条直角边就是直线 与x轴、y轴的交点与原点的距离.

10、一次函数y＝3x＋b的图象与两坐标轴围成的三角形面积是24，求b.

一次函数的性质的学案第四课时（）一次函数的性质及与不等式的关系

函数八

初二（ ）班 姓名：_________ 学号：____ 时间：2006年3月25日

[教学目标]使学生通过画图、观察、讨论，进一步归纳出一次函数的图象性质，并利用性质进行解题.

[教学重点]通过观察和讨论，把握一次函数的性质.

[教学过程]

环节一：继续探讨一次函数的图象性质

一、 请在同一个平面直角坐标系中画出了下列函数的图象

1、 y=2x－4 2

观察直线y=2x－4：

（1）图象与x轴的交点坐标是 ，与y轴的交点坐标是

（2）图象经过这些点：（-3， ） （-1， ） （0， ）

（ ，－2） （ ， 2）

（3）当x的值越来越大时，y的值越来越

（4）整个函数图象来看，是从左至右向 （填上升或下降）

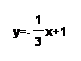（5）当x取何值时，y>0？

2、

观察直线y=－2x－2：

（1）图象与x轴的交点坐标是 ，与y轴的交点坐标是

（2）图象经过这些点：（-3， ） （-1， ） （0， ）

（ ，－4） （ ，－8）

（3）当x的值越来越大时，y的值越来越

（4）整个函数图象来看，是从左至右向 （填上升或下降）

（5）当x取何值时，y<0？

环节二：概括一次函数图象的性质

一次函数y＝kx＋b有下列性质：

（1） 当k＞0时，y随x的增大而______，这时函数的图象从左到右_____；

（2） 当k＜0时，y随x的增大而______，这时函数的图象从左到右_____.

（3）当b＞0时，这时函数的图象与y轴的交点在

（4）当b＞0时，这时函数的图象与y轴的交点在

环节三：课堂练习

[A组]

1、做一做，画出函数y=-2x 2的图象,结合图象

回答下列问题。函数y=-2x 2的图象中：

(1) 随着x的增大，y将 （填“增大”或“减小”）

(2) 它的图象从左到右 （填“上升”或“下降”）

(3) 图象与x轴的交点坐标是 ，与y轴的交点坐标是

(4) 这个函数中,随着x的增大,y将增大还是减小?它的图象从左到右怎样变化?

(5) 当x取何值时,y=0?

(6) 当x取何值时,y＞0?

2、函数y=3x－6的图象中：

（1）随着x的增大，y将 （填“增大”或“减小”）

（2）它的图象从左到右 （填“上升”或“下降”）

（3）图象与x轴的交点坐标是 ，与y轴的交点坐标是

3、已知函数y=(m-3)x- .

(1) 当m取何值时,y随x的增大而增大?

(2) 当m取何值时,y随x的增大而减小?

[B组]

1、写出一个y随x的增大而减少的一次函数

2、写出一个图象与x轴交点坐标为（3，0）的一次函数

3、写出一个图象与y轴交点坐标为（0，－3）的一次函数

第四课时的一课一练

[A组]

1.一次函数y=5x 4的图象经过___________象限,y随x的增大而________,它的图象与x轴. Y轴的坐标分别为________________ （2）．函数y=(k-1)x 2，当k＞1时，y随x的增大而______,当k＜1时，y随x的增大而_____。

2、函数y=-7x－6的图象中：

（1）随着x的增大，y将 （填“增大”或“减小”）

（2）它的图象从左到右 （填“上升”或“下降”）

（3）图象与x轴的交点坐标是 ，与y轴的交点坐标是

（4）x 取何值时，y=2? 当x=1时，y=

3.某个一次函数的图象位置大致如下图所示，试分别确定k、b的符号，并说出函数的性质.

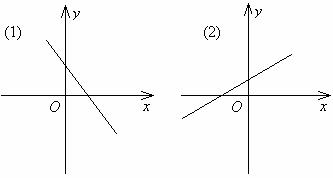
(k 0, b 0) (k 0, b 0)

4、已知一次函数y＝(2m-1)x＋m＋5,

当m取何值时,y随x的增大而增大?

当m取何值时,y随x的增大而减小?

5.已知点(x1, y1)和(x2, y2)都在直线 y= x-1上, 若x1 < x2, 则 y1__________y2

[B组]

6． 已知一次函数y＝(1-2m)x＋m-1，若函数y随x的增大而减小，并且函数的图象经过二、三、四象限,求m的取值范围.

7．已知函数 ,当m为何值时，这个函数是一次函数.并且图象经过第二、三、四象限？

8．已知一次函数y＝（1－2k） x＋（2k＋1）．

①当k取何值时，y随x的增大而增大？

②当k取何值时，函数图象经过坐标系原点？

③当k取何值时，函数图象不经过第四象限？

9.已知函数y＝2x-4.

(1)作出它的图象；

(2)标出图象与x轴、y轴的交点坐标；

(3)由图象观察，当-2≤x≤4时，函数值y的变化范围.

[C组]

10．若 a 是非零实数 , 则直线 y=ax-a 一 定（ ）

A.第一、二象限 B. 第二、三象限

C.第三、四象限 D. 第一、四象限

11.已知关于x的一次函数y＝(-2m＋1)x＋2m2＋m-3.

(1)若一次函数为正比例函数，且图象经过第一、第三象限，求m的值；

(2)若一次函数的图象经过点(1，-2),求m的值.

12． 已知一次函数y＝(3m-8)x＋1-m图象与y轴交点在x轴下方，且y随x的增大而减小，其中m为整数.

(1)求m的值；(2)当x取何值时，0＜y＜4？

函数九的学案第5课时（待定系数法）

初二（ ）班 姓名：_________ 学号：____ 时间：2005年3月31日

[教学目标]使学生通过实际问题，感受待定系数法的意义，并学会使用待定系数法求简单的函数关系式

[教学重点]使学生能应用待定系数法求一次函数的解析式，渗透常量与变量、已知和未知可以相互转化的思想方法

[教学过程]

环节一：试求一次函数解析式中的某些常量

1、水池已有水10m³，现以2m³/分钟的速度向水池注水，则水池中水的体积y（m³）与注水时间x（分钟）之间的函数关系式为

2、水池已有水bm³（b为常数），现以km³/分钟（k为常数）的速度向水池注水，则水池中水的体积y（m³）与注水时间x（分钟）之间的函数关系式为

（1）水池已有水bm³（b为常数），现以2m³/分钟的速度向水池注水，5分钟后水池中水的体积为25m³，则b= 。

（2）水池已有水15m³，现打开水管，以km³/分钟的速度向水池注水，5分钟后，水池中水的体积为30 m³，则k= 。

（3）水池已有水bm³（b为常数），现以km³/分钟（k为常数）的速度向水池注水，3分钟后水池中水的体积为16m³，8分钟后水池中水的体积为26m³，则

b= ，k= 。

环节二：例题练习

1、根据条件，求出下列函数的关系式：

（1） 函数y=kx（k≠O，K为常数）中，当x=2时，y=－6，则k= ，

函数关系式为y=

（2）直线y＝kx＋5经过点（－2，－1），则k= ，函数关系式为y=

（3）一次函数中，当x＝1时，y＝3；当x＝－1时，y＝7．

解：设所求函数的关系式是y＝kx＋b，根据题意，得

解得：

k=

b=

∴ 所求函数的关系式是

3、已知弹簧的长度 y（厘米）在一定的限度内是所挂重物质量 x（千克）的一次函数．现已测得不挂重物时弹簧的长度是6厘米，挂4千克质量的重物时，弹簧的长度是7.2厘米．求这个一次函数的关系式．

解：设所求函数的关系式是y＝ ，根据题意，得

解得： k=

b=

∴ 所求函数的关系式是

环节三：一课一 练

[A组]

1、根据下列条件写出相应的函数关系式．

（1）若直线y＝m＋1经过点（1,2），则该直线的解析式是

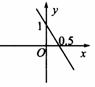
（2）一次函数y=kx b的图象如图所示，则k,b的值分别为（ ）

A.- ，1 B.-2，1 C. ，1 D.2，1

(3)已知一次函数的图象经过点A(－3，－2)和点B(1,6)．

①求此一次函数的解析式， 并画出图象；

②求此函数图象与坐标轴围成的三角形的面积．

(4)一次函数中，当x＝1时，y＝3；当x＝-1时，y＝7．

2、求满足下列条件的函数解析式：

（1）图象经过点（1，－2）的正比例函数的解析式；

(2)与直线y=－2x平行且经过点(1, -1)的直线的解析式；

(3)经过点（0，2）和（1，1）的直线的解析式；

(4)直线y=2x－3关于x轴对称的直线的解析式；

(5)把直线Y==2x 1向下平移两个单位，再向右平移3个单位后所得直线的解析

式．

[B组]

3、 已知y与x－3成正比例，当x＝4时，y＝3．

(1)写出y与x之间的函数关系式；

(2)y与x之间是什么函数关系；

(3)求x＝2.5时，y的值．

4、已知直线 的图象经过点（2，0），（4，3），（m，6），求m的值。

．

[C组]

5、点（1，1）、（2，0）、（3，－1）是否在同一条直线上？

6、 已知A、B两地相距30千米，B、C两地相距48千米．某人骑自行车以每小时12千米的速度从A地出发，经过B地到达C地．设此人骑行时间为x（时），离B地距离为y（千米）．

(1)当此人在A、B两地之间时，求y与x的函数关系及自变量x取值范围．

(2)当此人在B、C两地之间时，求y与x的函数关系及自变量x的取值范围．

分析 (1)当此人在A、B两地之间时，离B地距离y为A、B两地的距离与某人所走的路程的差．

(2)当此人在B、C两地之间时，离B地距离y为某人所走的路程与A、B两地的距离的差．

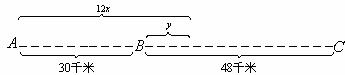
解 (1) y＝30－12x．(0≤x≤2.5)

(2) y＝12x－30．(2.5≤x≤6.5)

7、按照我国税法规定：个人月收入不超过800元，免交个人所得税．超过800元不超过1300元部分需缴纳5%的个人所得税．试写出月收入在800元到1300元之间的人应缴纳的税金y（元）和月收入x（元）之间的函数关系式．

．．

（应用）（可下一次用）

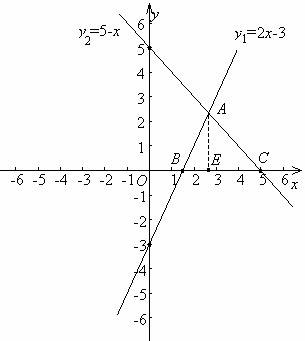
8、 已知两条直线y1＝2x-3和y2＝5-x．

(1)在同一坐标系内作出它们的图象；

(2)求出它们的交点A坐标；

(3)求出这两条直线与x轴围成的三角形ABC的面积；

(4)k为何值时，直线2k＋1＝5x＋4y与k＝2x＋3y的交点在每四象限．

分析 (1)这两个都是一次函数，所以它们的图象是直线，通过列表，取两点，即可画出这两条直线．

(2)两条直线的交点坐标是两个解析式组成的方程组的解．

(3)求出这两条直线与x轴的交点坐标B、C，结合图形易求出三角形ABC的面积．

(4)先求出交点坐标，根据第四象限内的点的横坐标为正，纵坐标为负，可求出k的取值范围．

解 (1)

(2) 解得

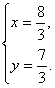
所以两条直线的交点坐标A为 ．

(3)当y1＝0时，x＝ 所以直线y1＝2x-3与x轴的交点坐标为B( ，0)，当y2＝0时，x＝5，所以直线y2＝5-x与x轴的交点坐标为C(5,0)．过点A作AE⊥x轴于点E，则 ．

(4)两个解析式组成的方程组为

解这个关于x、y的方程组，得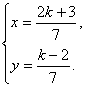

由于交点在第四象限，所以x＞0,y＜0．

即 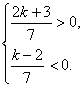解得 ．

例4 旅客乘车按规定可以免费携带一定重量的行李．假如所带行李超过了规定的重量，就要按超重的千克收取超重行李费．已知旅客所付行李费y（元）可以看成他们携带的行李质量x（千克）的一次函数为 ．画出这个函数的图象，并求旅客最多可以免费携带多少千克的行李？

分析 求旅客最多可以免费携带多少千克的行李数，即行李费为0元时的行李数．为此只需求一次函数与x轴的交点横坐标的值．即当y＝0时，x＝30．由此可知这个函数的自变量的取值范围是x≥30．

解 函数 (x≥30)图象为：

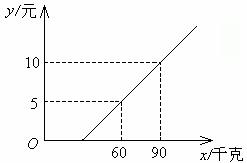
当y＝0时，x＝30.

所以旅客最多可以免费携带30千克的行李.

例5 今年入夏以来，全国大部分地区发生严重干旱．某市自来水公司为了鼓励市民节约用水，采取分段收费标准，若某户居民每月应交水费y（元）是用水量x（吨）的函数，当0≤x≤5时，y＝0.72x,当x＞5时，y＝0.9x-0.9．

(1)画出函数的图象；

(2)观察图象，利用函数解析式，回答自来水公司采取的收费标准.

分析 画函数图象时，应就自变量0≤x≤5和x＞5分别画出图象，当0≤x≤5时，是正比例函数，当x＞5是一次函数，所以这个函数的图象是一条折线.

解 (1)函数的图象是：

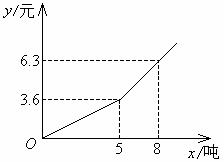
(2)自来水公司的收费标准是：当用水量在5吨以内时，每吨0.72元；当用水量在5吨以上时，每吨0.90元.

7、链接生活：某服装厂现有甲种布料42米，乙种布料30米，计划用这两种布料生产M，L两种型号的校服共40件．已知做一件M型号的服装需要甲种布料0.8米，乙种布料1.1米，可获利45元；做一件L型号的服装需要甲种布料1.2米，乙种布料0.5米，可获利30元．设生产M型号服装x件，用这批布料生产两种型号的服装所获的利润为Y元，

（1）写出y(元)与x(件)之间的函数关系式，并求出自变量的取值范围；

（2）该厂生产这批校服时，当M型号校服为多少件时，能使该厂所获的利润最大？最大利润是多少？

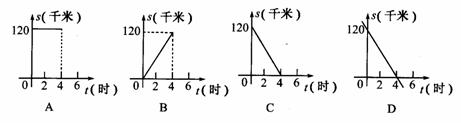
(4)汽车由天津驶往相距120千米的北京，它的平均速度是30千米/时，则汽车距北京的路程s（千米）与行驶的时间t(小时)的函数关系用图象应为下图中的（ ）

（多媒体演示幻灯片）

某学校需要刻录一批电脑光盘，若电脑公司刻录，每张需要8元（含空白光盘费）；若学校自刻，除租用刻录机需120元外，每张还需成本费4元（含空白光盘费）．问刻录这批

电脑光盘，到电脑公司刻录费用少，还是自刻费用少？你能帮助设计出一种使刻录费用最少的刻录方案吗？

2、课前热身