|
八年级上学期期末测试卷
班级:____________姓名:___________ 得分:___________
一、选择题(每小题2分,共20分)
1.下列计算正确的是( )
A. 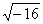 =-4 B.
=-4 B. 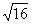 =±4
=±4
C. 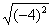 =-4 D.
=-4 D. 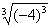 =-4
=-4
2.已知x有两个平方根,且|x|=3,则x的值为( )
A.9 B.3 C.-3 D.±3
3.用两个全等的直角三角形,拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形,其中不一定能拼成的图形是( )
A.①②③ B.②③
C.③④⑤ D.③④⑥
4.□ABCD的对角线AC上有两点E、F,且AE=EF=FC,则四边形BFDE的面积是 □ABCD面积的( )
A. 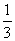 B.
B. 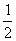 C.
C. 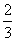 D.
D. 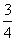
5.若直线y=-x a和直线y=x b的交点坐标为(m,8),则a b的值为( )
A.32 B.24 C.16 D.8
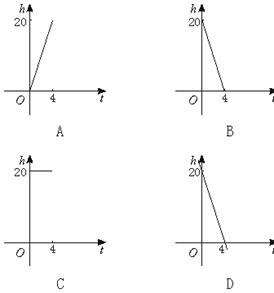
6.一根蜡烛长20 cm,点燃后每小时燃烧5 cm,燃烧时剩下的高度h(cm)与燃烧时间t(小时)的函数关系用图象表示为( )
7.若方程组 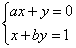 的解是
的解是 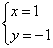 ,那么a,b的值为( )
,那么a,b的值为( )
A.a=1,b=0 B.a=1,b= 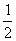
C.a=-1,b=0 D.a=0,b=0
8.某班有x人,分y个学习小组,若每组7人,则余下3人;若每组8人,则不足5人,求全班人数及分组数.正确的方程组为( )
A. 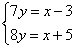 B.
B. 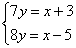
C. 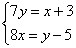 D.
D. 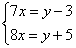
9.某轮船在顺水中行驶了3小时,每小时行驶m千米;在逆水中行驶了5小时,每小时行驶n千米,这艘轮船的平均速度为( )
A. 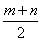 千米/时 B.
千米/时 B. 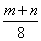 千米/时
千米/时
C. 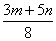 千米/时 D.
千米/时 D. 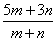 千米/时
千米/时
10.某校生物小组11人到校外采集标本,其中2人每人采集到6件,4人每人采集到3件,5人每人采集到4件,则这个小组平均每人采集标本( )
A.3件 B.4件 C.5件 D.6件
二、填空题(每小题2分,共20分)
11.|- 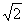 |的相反数是________.
|的相反数是________.
12. 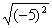 =________,
=________, 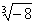 =_______.
=_______.
13.点P1(a-1,5)与点P2(2,b-1)关于x轴对称,则a b=________.
14.点A(3,-2)与点B(0,2)之间的距离为_______.
15.下列由火柴棒拼出的一列图形中,第n个图形由n个正方形组成,通过观察可以发现:
(1)第4个图形火柴棒的根数是________.
(2)第n个图形火柴棒的根数是________.

16.若直线y=kx-4,当x=-6时,y=8,那么k=________;假如这条直线又过点(9,m),则m=________.
17.直线y=(k2 1)x k,y随x的增大而________.(填“增大”或“减小”或“不变”)
18.已知 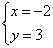 是方程x-ky=1的解,那么k=________.
是方程x-ky=1的解,那么k=________.
19.某班一组男生参加体育测试,引体向上成绩(单位:个)如下:6,9,11,13,11,7,10,8,12这组男生成绩的众数是________;中位数是________.
20.假如一个直角梯形的两底长分别为7 cm,12 cm,斜腰长为13 cm,那么这个梯形的面积等于_______.
三、解答题(21~23小题,每小题7分,24小题9分,25~27小题每小题10分,共60分)
21.一根弹簧,挂上物体后会伸长,弹簧总长y(cm)是所挂物体质量x(kg)的一次函数,其图象如图所示.
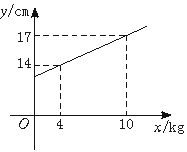
求:(1)y与x的函数关系式;
(2)弹簧原长是多少?
(3)若弹簧所挂物体质量不超过15 kg,那么弹簧最大可伸长到多少厘米?
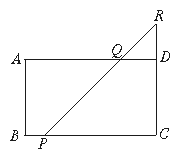
22.如图,在矩形ABCD中,AB=4,BC=7,P是BC边上与B点不重合的动点,过点P的直线交CD的延长线于R,交AD于Q(Q与D不重合),且∠RPC=45°,设BP=x,梯形ABPQ的面积为y,求y与x之间的函数关系,并求自变量x的取值范围.
23.列方程(组)解应用题
某校2002年秋季初一年级和高一年级招生总数为1000人,计划2003年秋初一年级招生数增 加20%,高一年级招生数增加15%,这样2003年秋季初一、高一年级招生总数比2002年将增加18%,求2003年秋季初一、高一年级计划招生数各是多少?
24.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)已知商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在(1)的方案中,为使销售时获利最多,你选择哪种进货方案?
25.某农户承包了山上的银杏树44株,现进入第三年收获时,先随意采摘5株树上的银杏称得每株树上的银杏质量如下(单位:千克):35,35,34,39,37.
(1)根据平均数估计,这年银杏的总产量是多少?
(2)若市场上的银杏售价每千克50元,则这年该农户卖银杏的收入将达到多少元?
26.甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下(单位:年):
甲厂:4,5,5,5,5,7,9,12,13,15;
乙厂:6,6,8,8,8,9,10,12,14,15;
丙厂:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)分别写出以上三组数据的平均数、众数、中位数;
(2)这三个厂家的推销广告分别用了哪一种表示集中趋势的特征数?
(3)假如你是顾客,宜选购哪家工厂的产品?为什么?
27.如图1,点E、F在正方形ABCD的边BC、CD上,且AE⊥BF于G.
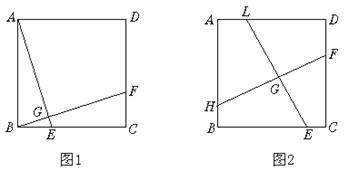
(1)AE与BF相等吗?请说明理由.
(2)运用图形的平移、旋转方法,分析说明△ABE和△BCF可以通过怎样的平移和旋转而相互得到.
如图2,点H、E、F、L在正方形ABCD的边上,且LE⊥HF于G,图2通过怎样的方法可以得到图1,从而分析说明LE与HF相等.
参考答案
一、1.D 2.B 3.D 4.A 5.C 6.B 7.A 8.A 9.C 10.B
二、11.- 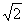 12. 5 -2 13.-1 14.5 15.13 3n 1 16.-2 -22 17.增大 18.-1 19.11 10 20.114 cm2
12. 5 -2 13.-1 14.5 15.13 3n 1 16.-2 -22 17.增大 18.-1 19.11 10 20.114 cm2
三、21.(1)y= 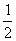 x 12 (2)12 cm (3)19.5 cm
x 12 (2)12 cm (3)19.5 cm
22.y=4x 8 0<x<3
23.600人 400人
24.(1)商场同时购进甲、乙两种电视机各25台;同时购进甲种电视机35台、丙种电视机15台;
(2)选择进甲种35台,丙种15台电视机的购货方案使销售时获利最多.
25.(1)1584千克 (2)79200元
26.(1)甲厂:8,5,6;乙厂:9.6,8,8.5;
丙厂:9.4,4,8
(2)甲厂选用平均数8;乙厂选用众数8;丙厂选用中位数8 (3)宜选购乙厂的产品,因为乙厂产品平均使用寿命最长且多数超过8年或达到8年寿命.
27.(1)AE=BF △ABE≌△BCF (2)略
|