一、仔细选一选（本题10小题，每小题3分，共30分）
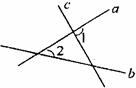
1. （ ）如图，射线c、b被直线a所截，则∠1与∠2是
A. 同位角 B. 内错角
C. 同旁内角 D. 对顶角
2. （ ）要使式子 
A．x>5 B．x>－5 C．x≥5 D．x≥－5
3. （ ）由5个相同的小立方体搭成的几何体如图所示，则它的左视图是
4. （ ）已知x＝2是方程 
A．3 B．4 C．5 D．6
5. （ ）给出下列调查：①了解市民对自来水质的满足程度；②了解学生对学校伙食的满足程度；③了解某路口在学校放晚学时段的车流量；④了解居民对废电池的处理情况；⑤防治某突发性传染病期间，某学校对学生测量体温，其中应作抽样调查的有
A. ②③④ B. ①②③④ C. ①②③⑤ D. ①②③④⑤
6. （ ）已知△ABC中，∠ACB＝90°，AC＝9cm，AB＝40cm则斜边上的中线CD的长是 A. 20cm B. 40cm C. 20.5cm D. 41cm
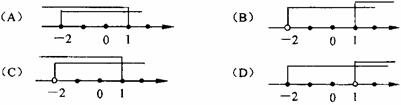
7. （ ）不等式组 
8. （ ）三角形两边长分别为3和6，第三边是方程 
A．11 B．13 C．11或13 D．11和13
9. （ ）根据下列表格的对应值：
|
x |
3.23 |
3.24 |
3.25 |
3.26 |
|
ax2 bx c |
－0.06 |
－0.02 |
0.03 |
0.09 |
判定方程ax2 bx c=0(a≠0，a, b, c为常数)一个解x的范围是
A．3＜x＜3.23 B．3.23＜x＜3.24
C．3.24＜x＜3.25 D．3.25＜x＜3.26
10.
|
|
|
|
|
|
|
|
|
|
（ ）如图.在宽为（A）
二、认真填一填（本题10小题，每小题3分，共30分）
11、把方程x(x－2)＝5x＋10化成一般式＿＿＿＿＿＿＿
12、方程 
13、写出一个无理数，使它与 
14、计算 
15、已知点P1(x1、y1)、P2(x2、、y2)在直线 
16.请写出一个根为x=1，另一根满足－1＜x＜1的一元二次方程__________________。
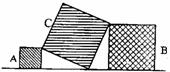
17、如图，三个正方形A、B、C如此放置，且正方形A、B的面积分别是2cm2和3cm2，则正方形C的面积等于________________cm2.
18、把点Q（－2，3）向上平移5个单位，再向左平移2个单位，则所得的像点Q'的坐标是＿＿＿＿＿＿。
19、某商场计划从2004年到2006年销售收入从20万元增长到28.8万元， 该商场销售收入每年的平均增长率是___________________。
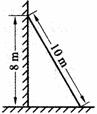
20、一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m。假如梯子的顶端下滑1m,梯子的底端滑动x米，可得方程＿＿＿＿＿＿＿＿。
三、耐心解一解（本题6小题，共计40分）下面每小题必须都有解题过程或推理步骤
21、(本题6分)计算：
(1) 
22、(本题6分)解方程：
(1) 
23、(本题5分)如图，在4×4正方形网格中的每个小正方形边长都是1，任意连结这些小正方形的顶点，可得到一些线段，请在图中画出AB= 
24、（7分）如图△ABC中，点D在AC上，E在AB上，且AB=AC，BC=CD，AD=DE=BE。
（1）求证△BCE≌△DCE；
（2）求∠EDC的度数。
25、(本题8分)某商场将进货价为30元的台灯以40元售出，平均每月能售出600个。调查表明：这种台灯的售价每上涨1元，其销售量就将减少10个。为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应进台灯多少个？请你利用方程解决这一问题。
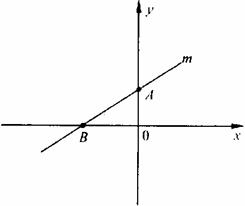26、(本题8分)如图，直线m与x轴、y轴分别交于点B、A，且A、B两点的坐标分别为A(0,3)、B(－4,0)。
(1) 请求出直线m的函数解析式；
(2) 在x轴上是否存在一点C，使△ABC为等腰三角形？若存在，请求出点C的坐标(不需要具体的解题过程)，并在坐标系中标出点C的大致位置；若不存在，请说明理由。
