(时间；45分钟 满分：100分)

班级_______姓名_______学号_______得分_______

一、选择题(本题共8小题，每小题3分，共24分．下列各题都有代号为A，B，C，D的四个结论供选择，其中只有一个结论是正确的)

1，下列计算正确的是 ( )

A．(ab4)4＝a4b8 B．(a2)3÷(a3)2＝0 C. (－x)6÷(－x3)＝－x3 D. －x2y3×100＝0

2．下列各式可以分解因式的是 ( )

A．x2－(－y2) D．4x2＋2xy＋y2 C －x2＋4y2 D．x2－2xy－y2

3．如下图所示，一辆客车从甲站驶往乙站，中途休息了一段时间．假如用横轴表示时间t，纵轴表示客车行驶的路程s，那么下列四个图中较好地反映了s与t之间的函数关系的是 ( )

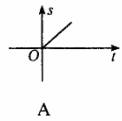
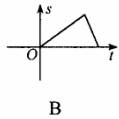
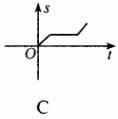
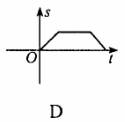
4．下列四个条件，可以确定△ABC与△A1B1C1全等的是 ( )

A．BC＝B1C1、AC＝A1C1、∠A＝∠B1 B．AB＝AC、A1B1＝A1C1、∠A＝∠A1

C. AC＝A1C1、∠A＝∠A1、∠B＝∠B1 D．∠A＝∠A1、∠B＝∠B1、∠C＝∠C1

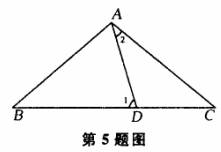
5．如下图所示，D为BC上一点，且AB＝AC＝BD．则图中∠1与∠2的关系是( )

A．∠1＝2∠2 B．∠1＋∠2＝180°

C．∠1＋3∠2＝180° D．3∠1－∠2＝180°

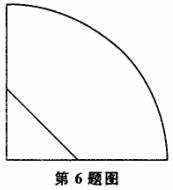
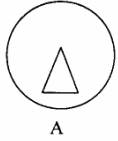
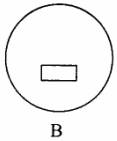
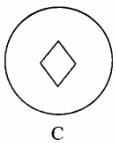
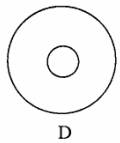
6．把一圆形纸片对折后再对折，得到此图，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是 ( )

7．若A(x1，y1)，B(x2，y2)为一次函数y＝3x－1的图象上的两个不同的点，且x1x2≠0，设M＝ eq \f(y1＋1,x1)，N＝ eq \f(y2＋2,x2)，那么M与N的大小关系是 ( )

A．M＞N B．M＜N C. M＝N D．不确定

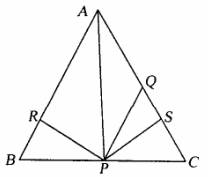
8．如图，在△ABC中，AQ＝PQ，PR＝PS，PR⊥AB于R，PS⊥AC于S，则三个结论①AS＝AR ②QP∥AR ③△BPR≌△QSP中 ( )

A．全部正确 B．仅①和②正确 C．仅①正确 D．仅①和③正确

二、填空题(本题共8小题；每小题3分，共24分．把最后结果填在题中横线上)

9．若5x2ym与4xn＋m－1y的和是单项式，则代数式m2－n的值是_______。

10．若9x2－kxy＋4y2是一个完全平方式，则k的值是_______。

11．若点P(a，b)在第二象限内，则直线y＝ax＋b不经过第_______限．

12．把直线y＝ eq \f(2,3)x＋1向上平移3个单位所得到的解析式为_______。

13．在扇形统计图中，有两个扇形的圆心角度数之比为3∶4，且知较小扇形表示24本课外书，那么较大扇形表示_______本课外书．

14．若等腰三角形的顶角为100°，则它腰上的高与底边的夹角是_______。

15．若y＋6与x＋a(a，b是常数)成正比例，且当x＝3时，y＝5，当x＝2时，y＝2，则y与x的函数关系是_______。

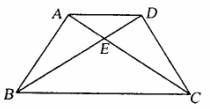
16．如右图，∠BAC＝∠CDB＝90°，BE＝EC，则图中的全等三角形有_______对，

三、解答题(共52分)

17．(4分)计算：(a2＋ab＋b2)(a2－ab＋b2)．

18．(4分)先化简，再求值：

(2a－3b)2－(3b＋2a)2，其中a＝－ eq \f(1,4)，b＝3．

19．(12分)因式分解：

(1) eq \f(1,3)－3a2； (2)9(x＋y)2－4(x－y)2；(3)(x＋y)2－4(x＋y－1)； (4)－x2y＋2xy2－y3．

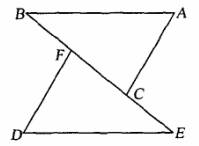
20．(4分)已知，如图，点B、F、C、E在同一直线上，FB＝CE，AB∥ED，AC∥FD．

求证：AB＝ED，AC＝DF．

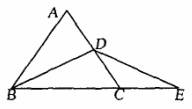
21．(7分)已知，如图，等边△ABC中，D为AC的中点，CE为BC的延长线，且CE＝CD．

求证：BD＝DE．

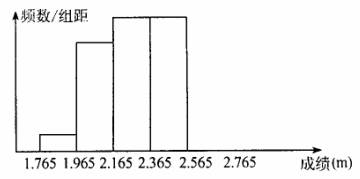
22．(7分)某校500名男生参加体育中考立定跳远测试，将所得成绩整理后分成五组，画出部分频率分布直方图，已知图中从左到右前四个小组的频率依次是0.04,0.24，0.28，0.28．

(1)求第五小组的频率，并补全频率分布直方图；

(2)若规定2.165m以上为满分，试问该校男生立定跳远得满分的人数有多少?

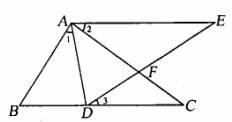
23．(7分)如图，点E在△ABC外部，点D在边BC上，DE交AC于F．若∠1＝∠2＝∠3，AC＝AE，请说明△ABC≌△ADE的道理．

24．(7分)某苹果生产基地组织20辆汽车装运A，B，C三种苹果42吨到外地销售．按规定每辆车只装一种苹果，且必须装满，每种苹果不少于2车．

苹果品种

A

B

C

每辆汽车的装载重量(吨)

2.2

2.1

2

每吨苹果获利(百元)

6

8

5