八年级下期中测试卷华师大版

一．选择题（每题3分，共24分）

1. 下列各式正确的是（ ）

A eq \r(,36)=±6 B - eq \r(3,-8) =-2 C eq \r(,（-6）2)=-6 D eq \r(3,-7)=- eq \r(3,7)

2. - eq \r(3,-64)的平方根是（ ）

A ±4 B 2 C ±2 D 不存在

3. 如图，已知△ABC，P为AB上一点，连结CP，以下各条件中不能判定△ACP∽△ABC的是（ ）

A ∠ACP=∠B B ∠APC=∠B

C eq \f(AC,AP)= eq \f(AB,AC) D eq \f(AC,AB)= eq \f(CP,BC)

4. 化简 eq \r(, eq \f(12,x))的结果是（ ）

A eq \f(2,x) eq \r(,3) B eq \f(,) eq \f(2,x) eq \r(,3x) C 2x eq \r(,2x) D eq \f(3,x) eq \r(,2x)

5. 下列给出的四个点中，不在直线y=2x-3上的是（ ）

A （1， -1） B （0， -3） C （2， 1） D （-1，5）

6. 汽车开始行驶时，油箱内有40升油，则油箱内剩余油量Q（升）与行驶时间t（时）

的函数关系式为（ ）

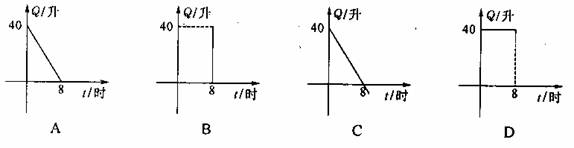
7. 若反比例函数y= eq \f(2m-1,x)，y随x的增大而减小，则m的取值范围是（ ）

A m> eq \f(1,2) B m< eq \f(1,2) C m>- eq \f(1,2) D m<- eq \f(1,2)

8. 无论m取任何非零实数,一次函数y=mx-(3m 2)的图象过定点（ ）

A (3,2) B (3,-2) C (-3,2) D (-3,-2)

二、填空题(每空2分，共25分)

9. eq \r(,(-3)2)= ,64的立方根为 , eq \f(1,3)和- eq \f(1,3)是 的平方根.

10. 若 eq \r(,x)= eq \f(1,5) ,则x= ,平方根得10-4的数是 .

11. 算术平方根等于它本身的数是 ,平方等于它本身的数是 ,立方等于它本身的数是 .

12. 假如两个三角形相似,相似比为5:8,则对应高的比为 ,周长比等于 ,面积比等于 .

13. 若整数x满足关系式- eq \r(,3)<x< eq \r(,6),则x= .

14. 在实数 eq \f(22,7), eq \r(,8),0.3, eq \f(π,2), eq \r(,9), eq \r(3,216),1- eq \r(,3)中,正无理数有 .

15. 假如(x 1)2 eq \r(,y-3)=0,则x 2y= .

16. 我们已经知道 eq \r(,2)是一个无理数,请写出三个比 eq \r(,2)还要小的正无理数,其中一个是不带根号的无理数: .

17. 用计算器探求:满足使 eq \r(, eq \f(n 1,n))的值小于1.01的最小正整数n= .

18. ⑴ 函数y= eq \f(1,5-x)中自变量x的取值范围是 .

⑵ 在一次函数y=(a 2)x 8的图象上有一点P,且点P的坐标为(-1,2),则a的取值范围是 .

19. 点A(a,-5)和(3,b)关于x轴对称,则a= ,b= .

20. 茶叶蛋每个0.55元,小明和同学们一起买的茶叶蛋个数x与所付出的钱数y(元)之间的函数关系式为 ,自变量x的取值范围是 .

21. 一次函数y=（2-k）x 2（k为常数），y随x的增大而增大，则k的取值范围是 .

22. 如图，EC∥AB，ED∥BC，图中有三对相似三角形，它们分别是 .

23. 如图,A、B分别是MP、MQ的中点,C、D分别是AP、BQ的中点,且AB∥CD∥PQ,则

S△MAB:S△MCD:S△MPQ= .

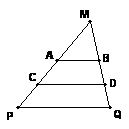
(第22题图) （第22题图)

四、化简与求值(24题16分,25题8分,共24分)

24. ⑴ eq \r(,8)- eq \r(,4)- eq \r(,18) ⑵ (1-2 eq \r(,3))2

⑶ 3 eq \r(, eq \f(1,2))- eq \r(,32) eq \r(,2) ⑷ eq \f( eq \r(,50) eq \r(,32), eq \r(,8))-4

25. 求x的值.

⑴ 27(x-2)3=8 ⑵ 3(x 1)2-(4 eq \r(,3))2=0

五、解答题(26、27题每题6分,28题8分,29题7分,共27分)

26. 如图,是一个3×3的格点三角形,三个顶点都在小正方形上的三角形叫做格点三角形.

⑴ 请在图中画出一个格点△ABC,使它的边长分别为 eq \r(,2)、2 eq \r(,2)、 eq \r(,10);

⑵ 在图中再画出一个格点三角形,使△EFG∽△ABC,且他们的相似比为1: eq \r(,2),并说明他们相似的理由.

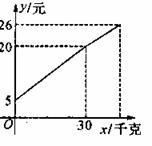
27. 一农民带了若干千克土豆进城出售,为了方便,他带了一些零用钱备用,按市场价出售一些土豆后,又降价出售,兽出土豆的千克数与他手中持有的钱数(含备用钱)的关系如图.结合图象回答:

⑴ 农民自带的零钱是多少?

⑵ 降价前他每千克土豆出售的价格是多少?

⑶ 降价后他按每千克0.4元将土豆售完,这时他手中的钱(含备用钱)是26元,问他一共带了多少土豆去城里出售?

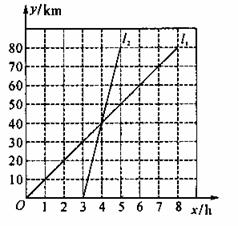
28. 如图，表示一骑自行车和一骑摩托车者沿相同的路线由甲地到乙地行驶过程的函数图象，两地相距80千米，请根据图象解决下列问题：

⑴ l1是 行驶过程的函数图象，l2是 行驶过程的函数图象；

⑵ 哪一个人出发早？早多长时间？哪一个人早到达目的地？早多长时间？

⑶ 求出两个人在途中行驶的速度是多少？

⑷ 分别求出表示自行车和摩托车行驶过程的函数解析式，并求出自变量x的取值范围。

29. 正方形ABCD的边长为4，将此正方形置于平面直角坐标系中，使AB边落在X轴的正半轴上，且A点的坐标是（1，0）。

⑴ 直线y= eq \f(4,3)x- eq \f(8,3)经过点C，且与x轴交与点E，求四边形AECD的面积；

⑵ 若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式，并在图中画出直线l.