|
九年级复习考试数学试题参考答案及评分标准
一、选择题(每小题2分,共20分)
1.B 2.C 3.D 4.D 5.A 6.D 7.A 8.A 9.C 10.C
二、填空题(每小题3分,共18分)
11. -2 12. 2<x<8 13. x+1 14. 2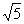 15. 2 15. 2 16. 16. 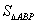
三、解答题(每小题5分,共20分)
17.解:原式4-1-2=1 18. ①Q ②X ③Z ④D ⑤M
19.解:设杯子和暖壶的单价分别是x元、y元,则有
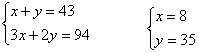
答:杯子和暖壶的单价分别是8元、35元.
20.
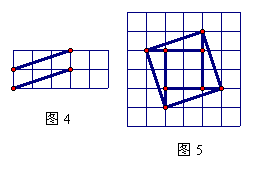
注: 图4和图5的分值分别为2分和3分
四、解答题(每小题6分,共18分)
21.解:由旋转的性质可知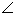 PA PA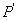 = =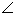 BAC= BAC= , ,
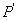 A=PA= A=PA= . P . P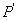 =2. 答: PP/的长为2. =2. 答: PP/的长为2.
22.解:延长AD,BC交于点F,过D做DE⊥CF于E,
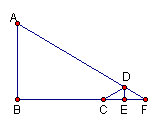
则DE=4米,CE=EF=4 米,-------3分 米,-------3分
设AB=x米由DE//AB知△FDE∽△FAB得
DE:AB=FE:FB 4: x=4 : (20+8 : (20+8 ) )
x= 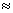 19.5(米) . 19.5(米) .
答:旗杆高19.5米.----------------------6分
23.(1)∵15-6 = 9,
∴ 四月份用水量的极差是9吨.------2分
(2)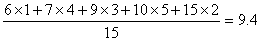 (吨), (吨),
∴阳光居民小区四月份每户家庭的月平均用水量大约为9.4吨.-------------------------4分
(3)如图:---------------------------------------6分
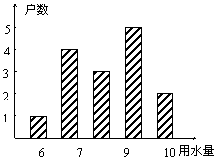
五、解答题(每小题8分,共24分)
24.(1)由题意得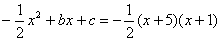 , ,
展开后比较系数,得 b =-3, , 即关系式为 , 即关系式为 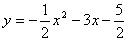 .------3分 .------3分
∵  ,∴ 其大致图象(略).--------------6分 ,∴ 其大致图象(略).--------------6分
(2)先向下平移2个单位,再向右平移3个单位;或先向右平移3个单位,再向下平移2个单位.----------------------------------------8分
25.(1)∵ΔΑΒC是等腰直角三角形,D是AB的中点,∴DA=DC,∠A=∠DCN=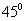 . .
又∵∠AMD+∠MDC=∠NDC+∠MDC= ∴∠ADM=∠NDC , ∴∠ADM=∠NDC ,
∴ΔADM≌ΔCDN, ∴DM=DN.---------------------4分
(2)如图所示,∵DC=DB,∠DCM=∠DBN=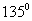 , ,
∠CDM=∠BDN,∴ΔDCM≌ΔDBN,∴DM=DN.---8分

26.解:①当点P在AB边上运动时,0<x<1,
此时AP=x, =y= =y=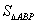 ?x?1= ?x?1=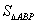 x. x.
当y=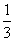 时,解得x= 时,解得x=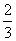 .--------------2分 .--------------2分
②当点P在BC边上运动时,1<x<2,
此时折线ABP=x-1,PC=2-x.
 =y= =y=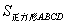 - -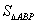 - - - -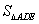 =1- =1-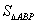 (x-1)?1- (x-1)?1-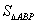 (2-x)? (2-x)?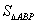 - - = =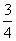 - - x. x.
当y=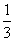 时,解得x= 时,解得x= ,------------------4分 ,------------------4分
③当点P在CE边上时,S△CEA=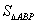 ? ?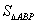 ?1= ?1= < <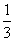 , ,
所以这时 < <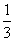 .不存在S△APE = .不存在S△APE =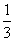 .-----6分 .-----6分
综上所述,当x=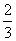 或x= 或x= 时,△APE的面积为 时,△APE的面积为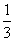 .-------8分 .-------8分
27.⑴A、B的坐标分别是(6,0),(0,8). ----------------------2分
⑵由BO=8,AO=6,得AB=10.当移动时间为t时,AP=t,AQ=10-2t.
∵∠QAP=∠BAO,
∴当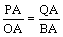 时,△APQ∽△AOB. 时,△APQ∽△AOB.
∴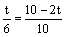 ,∴t= ,∴t= (秒). (秒).
∵∠QAP=∠BAO,
∴当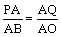 时,△AQP∽△AOB. 时,△AQP∽△AOB.
∴ ,∴t= ,∴t=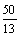 (秒). (秒).
∴t= 秒或t= 秒或t=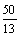 秒,经检验,它们都符合题意,此时△AQP与△AOB相似. ----------------------6分 秒,经检验,它们都符合题意,此时△AQP与△AOB相似. ----------------------6分
⑶当t=  秒时,PQ∥OB,PQ⊥OA,PA= 秒时,PQ∥OB,PQ⊥OA,PA= , ,
∴OP=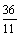 ,∴P( ,∴P(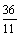 ,0). ,0).
∴线段PQ所在直线的函数表达式为x=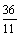 . .
当t=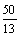 时,PA= 时,PA=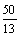 ,BQ= ,BQ=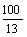 ,OP= ,OP= ,∴P( ,∴P( ,0). ,0).
设Q点的坐标为(x,y),则有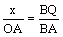 , ,
∴ ,∴x= ,∴x=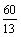 . .
当x=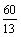 时,y=- 时,y=-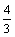 ? ?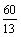 +8= +8=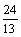 ,∴Q的坐标为( ,∴Q的坐标为(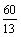 , ,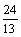 ). ).
设PQ的表达式为y=kx+b,则 ∴ ∴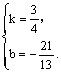
∴PQ的表达式为y=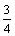 x- x-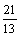 .-----------------------------------------10分 .-----------------------------------------10分
28.不能为 .----------------------------------------------1分 .----------------------------------------------1分
取AB、HG的中点M、N,连结MN、MH.
在△BMH中,?BMH = 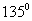 ,∴ ? MBH + ?MHB = ,∴ ? MBH + ?MHB = 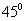 , ,
又 MH>MB,∴ ?MBH>?MHB,
∴ ?MBH>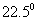 . .
∴ 4?ABH> , ,
∴ 按方案三所焊接而成的大扇形的圆心角必大于90°,---------5分
(2)不能相等,面积增大.
∵ 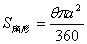 ,由于 ,由于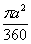 为常数且大于零, 为常数且大于零,
∴ 圆心角q 增大,扇形的面积必增大.-------------------------8分
(3)n越大,所焊接成的大扇形的面积也越大.
∵ n越大,焊接而成的大扇形的圆心角越大 .------------------------10分
|