|
二元一次方程组中出现字母系数(包括字母常数),是我们经常碰到的问题,它比单纯解方程组要求高一些。解此类问题首先要进行分析,挖掘题目所隐含的条件,运用转化的数学思想,巧妙地列出相应的方程或方程组来解,请看下面的例子。
例1 若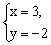 是二元一次方程组 是二元一次方程组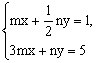 的解,求m、n的值。 的解,求m、n的值。
分析:根据方程组解的定义,可把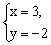 代入方程组中,这样可得到关于m、n的二元一次方程组,解之即可。 代入方程组中,这样可得到关于m、n的二元一次方程组,解之即可。
解:把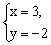 代入相应的二元一次方程组中,得 代入相应的二元一次方程组中,得 解得 解得
例2 已知方程组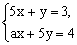 与 与 有相同的解,求a、b的值。 有相同的解,求a、b的值。
分析:两个方程组的解相同,也就是有一组x、y的值是这四个方程的公共解,当然也是其中任意两个方程的公共解。所以可以把原来的方程组打乱,重新组合起来求解。
解:由已知可得 解得 解得
把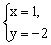 代入剩下的两个方程组成的方程组 代入剩下的两个方程组成的方程组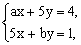 得 得 解得 解得
例3 关于x、y的方程组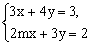 的解中x与y的和等于1,则m的值是 。 的解中x与y的和等于1,则m的值是 。
分析:方程组的解也必然是方程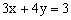 的解,也是方程 的解,也是方程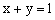 的解,把它们组合得方程组 的解,把它们组合得方程组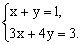 这个方程组的解一定也是方程 这个方程组的解一定也是方程 的解,代入这个方程即可求得m的值。 的解,代入这个方程即可求得m的值。
解:由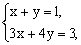 解得 解得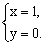
代入 ,得 ,得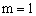 。 。
例4 k为何值时方程组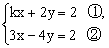 无解? 无解?
分析:将方程组消元,使之化为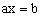 的形式,然后讨论一次项系数a。当 的形式,然后讨论一次项系数a。当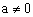 时,有唯一解 时,有唯一解 ;当 ;当 , ,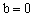 时,有无数个解;当 时,有无数个解;当 , ,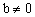 时,无解。反之也成立。 时,无解。反之也成立。
解:①×2+②,得 。 ③ 。 ③
由原方程组无解,知方程③也无解。所以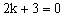 。解得 。解得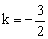 。当 。当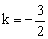 时方程组无解。 时方程组无解。
例5 小刚在解方程组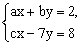 时,本应解出 时,本应解出 由于看错了系数c,而得到的解为 由于看错了系数c,而得到的解为 求 求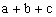 的值。 的值。
分析:尽管看错了c,但是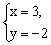 和 和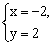 都适合方程组中的第一个方程。将它们代入第一个方程可得到关于a、b的二元一次方程组,可解出a、b的值,再由原方程组的解是 都适合方程组中的第一个方程。将它们代入第一个方程可得到关于a、b的二元一次方程组,可解出a、b的值,再由原方程组的解是 可求出c的值。 可求出c的值。
解:∵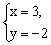 是方程组 是方程组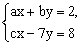 的解, 的解,
∴
由方程②,得 。 。
设小刚把c看成了n,则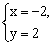 满足 满足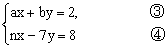
由③可得 。 ⑤ 。 ⑤
由方程①⑤组成方程组 解得 解得
所以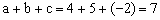 。 。
例6 要使方程组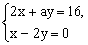 有正整数解,求整数a的值。 有正整数解,求整数a的值。
分析:首先解方程组(用含a的式子表示x、y的取值),再由条件确定a的取值。
解:解方程组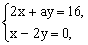 得 得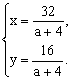
要使x、y均为正整数,则a+4必须是16和32的正整数因数,所以a+4只能等于1,2,4,8,16,故整数a的值是-3,-2,0,4,12。
[练一练]
1、方程组 的解中x与y相等,则k= 。 的解中x与y相等,则k= 。
2、在二元一次方程组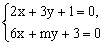 中,当m= 时,这个方程组有无数组解。 中,当m= 时,这个方程组有无数组解。
3、已知关于x、y的方程组 的解是 的解是 求a+b的值。 求a+b的值。
4、已知关于x、y的方程组 的解也是方程 的解也是方程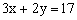 的解,求m。 的解,求m。
5、小明和小言同时解方程组
小明把方程①抄错了,求得的解为 小言把方程②抄错了,求得的解为 小言把方程②抄错了,求得的解为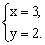 求原方程组的解。 求原方程组的解。
答案:1、0 2、9 3、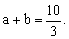 4、m=1。 5、 4、m=1。 5、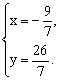
|