|
中考数学二轮复习题精选
(第五辑)
 1、如图,地面上有不在同一直线上的A、B、C三点,一只青蛙位于地面异于A、B、C的P点,第一步青蛙从P跳到P关于A的对称点P1,第二步从P1跳到P1关于B的对称点P2,第三步从P2跳到P2关于C的对称点P3,第四步从P3跳到P3关于A的对称点P4……以下跳法类推,青蛙至少跳几步回到原处P.( ) 1、如图,地面上有不在同一直线上的A、B、C三点,一只青蛙位于地面异于A、B、C的P点,第一步青蛙从P跳到P关于A的对称点P1,第二步从P1跳到P1关于B的对称点P2,第三步从P2跳到P2关于C的对称点P3,第四步从P3跳到P3关于A的对称点P4……以下跳法类推,青蛙至少跳几步回到原处P.( )
 A.4 B.5 C.6 D.8 A.4 B.5 C.6 D.8
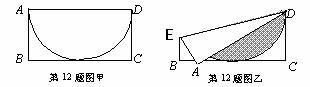
2、有一张矩形纸片ABCD,其中AD=4cm,上面有一个以AD为直径的半园,正好与对边BC相切,如图(甲)。将它沿DE折叠,是A点落在BC上,如图(乙)。这时,半圆还露在外面的部分(阴影部分)的面积是( )
A、(π-  )cm2 B、(
)cm2 B、( 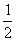 π+
π+ 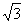 )cm2 C、(
)cm2 C、( 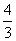 π-
π- 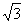 )cm2 D、(
)cm2 D、(  π+
π+ 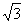 )cm2
)cm2
 3、已知函数y=x-5,令x= 3、已知函数y=x-5,令x= 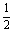 、1、
、1、 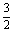 、2、
、2、 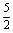 、3、
、3、 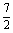 、4、
、4、 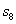 、5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1)、Q(x2,y2),则P、Q两点在同一反比例函数图象上的概率是( )
、5,可得函数图象上的十个点.在这十个点中随机取两个点P(x1,y1)、Q(x2,y2),则P、Q两点在同一反比例函数图象上的概率是( )
(A) 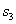 (B)
(B) 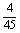 (C)
(C) 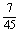 (D)
(D) 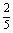
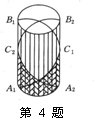
4、编织一个底面周长为a、高为b的圆柱形花架,需用沿圆柱
表面绕织一周的竹条若干根,如图中的A1C1B1,A2C2B2,  \* MERGEFORMAT
, 则
\* MERGEFORMAT
, 则
每一根这样的竹条的长度最少是 ( )
A. 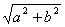 B.
B. 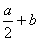 C.
C. 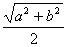 D.
D. 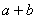
5、已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于 ( )
A.50 B.49 C.-50 D.-48
6、如图20,已知四边形ABCD的对角线AC=BD,AC⊥BD,四边形A1B1C1D1的四个顶点A1、B1、C1、D1分别为AB、BC、CD、DA的中点,四边形A2B2C2D2的四个顶点A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,假如AC=2a,那么S四边形AnBnCnDn=______________
 

7、如图5,在等腰△ABC中,∠C=90º,BC=2 cm,假如以AC的中点O为旋转中心,将这个三角形旋转180º,点B落在点B´处,那么点B´与点B原来位置相距 .
8、刘先生买了一套住房,并对房屋进行装修,工人师傅用半径为10 cm的圆形地板打磨机打磨地板,如图所示阴影部分表示一个墙角打磨不到的面积,那么一个矩形房间的地板打磨不到的面积为__________平方厘米.(π取3)
 9、如图,假如以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积 9、如图,假如以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积 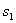 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为 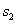 ,
, 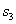 ,…..,
,…..,  (n为正整数),那么第8个正方形的面积
(n为正整数),那么第8个正方形的面积 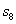 =_______。
=_______。
10、一只昆虫从点A处出发,以每分钟2米的速度在一条直线上运动,它先前进1米,再后退2米,又前进3米,再后退4米,……依此规律继续走下去,则运动1小时时这只昆虫与A点相距___________米.
11、如图,将半径为1、圆心角为 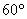 的扇形纸片
的扇形纸片  ,在直线
,在直线  上向右作无滑动的滚动至扇形
上向右作无滑动的滚动至扇形 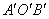 处,则顶点
处,则顶点 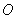 经过的路线总长为 。
经过的路线总长为 。
12、(1)观察右边的一列数: 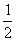 ,
, 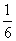 ,
,  ,
, 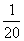 ,
, 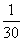 ,
, 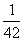 ,……,根据其规律可知:
,……,根据其规律可知:
第7个数是 , 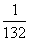 是第 个数,第
是第 个数,第 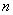 个数是
个数是  为正整数)。
为正整数)。
(2)观察图①~④中阴影部分构成的图案:

① ② ③ ④ ⑤ ⑥
 请写出这四个图案都具有的两个共同特征: ; 。并在图⑤、⑥中各设计一个新的图案,使该图案同时具有图①~④中的两个共同性质。 请写出这四个图案都具有的两个共同特征: ; 。并在图⑤、⑥中各设计一个新的图案,使该图案同时具有图①~④中的两个共同性质。
13、如图,在直角坐标系中,直线 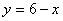 与
与 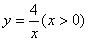 的图像相交于点A、B,设点A的坐标为
的图像相交于点A、B,设点A的坐标为  ,那么长为x1,宽为y1的矩形面积和周长分别为( )
,那么长为x1,宽为y1的矩形面积和周长分别为( )
A、4,12 B、8,12 C、4,6 D、8,6
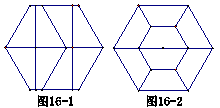 14、某校九年级学生开展了丰富多彩的数学课题学习活动。在探讨《漂亮的正六边形》课题学习时,发现正六边形可以分成八个全等的直角梯形(如图16-1),也可以分成八个全等的等腰梯形(如图16-2),则直角梯形的最短边与等腰梯形的最短边的比值是 . 14、某校九年级学生开展了丰富多彩的数学课题学习活动。在探讨《漂亮的正六边形》课题学习时,发现正六边形可以分成八个全等的直角梯形(如图16-1),也可以分成八个全等的等腰梯形(如图16-2),则直角梯形的最短边与等腰梯形的最短边的比值是 .
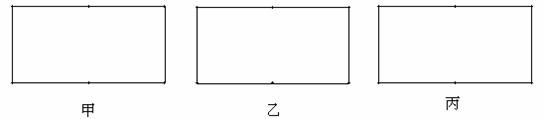
15、图有一矩形纸片,已知长是宽的2倍。把这个矩形分别剪成:
(1) 两部分,使得能用它们拼成一个等腰三角形(图甲);
(2) 两部分,使得能用它们拼成一个等腰梯形(图乙)
(3) 三部分,使得能用它们拼成一个正方形(图丙)
请按上述要求在对应图中画出拼成图形的示意图。
 16、在一张长为9厘米,宽为8厘米的矩形纸板上,剪下一个腰长为5厘米的等腰三角形(要求等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上),请你计算剪下的等腰三角形的面积? 16、在一张长为9厘米,宽为8厘米的矩形纸板上,剪下一个腰长为5厘米的等腰三角形(要求等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上),请你计算剪下的等腰三角形的面积?
17、已知,如图,等边三角形ABC边长为2,以BC为对称轴将 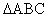 翻折,得到四边形ABDC,将此四边形放在直角坐标系xoy中,使AB在x轴上,点D在直线
翻折,得到四边形ABDC,将此四边形放在直角坐标系xoy中,使AB在x轴上,点D在直线 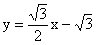 上。
上。
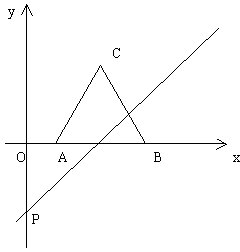
(1)根据上述条件画出图形,并求出A、B、D、C的坐标;
(2)若直线 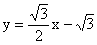 与y轴交于点P,抛物线
与y轴交于点P,抛物线  ,过A、B、P三点,求这条抛物线的函数关系式。
,过A、B、P三点,求这条抛物线的函数关系式。
(3)求出抛物线的顶点坐标,并指出这个点在  的什么非凡位置。
的什么非凡位置。
18、如图,在直角坐标系中,半径为2cm的动圆M与  轴交于A、B两点,且保持弦AB长为定值2cm,圆M与
轴交于A、B两点,且保持弦AB长为定值2cm,圆M与 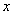 轴没有交点,且圆心M在第一象限内,P是
轴没有交点,且圆心M在第一象限内,P是 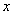 轴正半轴上一动点,MQ
轴正半轴上一动点,MQ 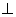 AB于Q,且MP=3cm,设OA=
AB于Q,且MP=3cm,设OA= 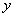 cm,OP=
cm,OP= 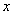 cm。
cm。
(1)求 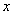 、
、 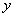 所满足的关系式,并写出
所满足的关系式,并写出 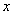 的取值范围;
的取值范围;
(2)当  MOP为等腰三角形时,求相应
MOP为等腰三角形时,求相应 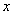 的值;
的值;
 (3)是否存在大于2的实数 (3)是否存在大于2的实数 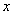 ,使
,使  MQO∽
MQO∽  OMP?若存在,求出相应的值;若不存在,请说明理由。
OMP?若存在,求出相应的值;若不存在,请说明理由。
中考数学二轮复习题精选
(第五辑参考答案)
1、C 2、C 3、B 4、A 5、C 6、  7、
7、 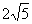 cm 8、100
cm 8、100
9、128 10、8 11、(略) 12、(略) 13、A 14、 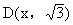 15、(略)
15、(略)
16、 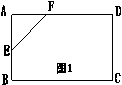 解:分三种情况计算: 解:分三种情况计算:
⑴当AE=AF=5厘米时(图一)
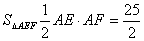 …………………(4分)
…………………(4分)
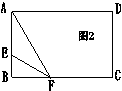 ⑵当AE=EF=5厘米时(图2) ⑵当AE=EF=5厘米时(图2)
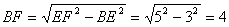
∴ 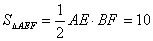 …………(3分)
…………(3分)
 ⑶当AE=EF=5厘米时(图3) ⑶当AE=EF=5厘米时(图3)
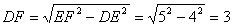
∴ 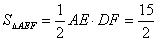 …………(3分)
…………(3分)
17、解:(1)依题意,四边形ABDC为菱形
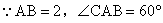
 C、D两点纵坐标均为
C、D两点纵坐标均为 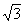
 设 设 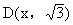
 点D在直线
点D在直线 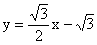 上
上 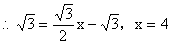
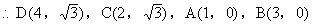
如图 ……4分
(2) 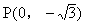 ,抛物线过A、B、P三点
,抛物线过A、B、P三点
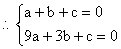
解得 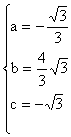
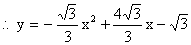 ……6分
……6分
(3) 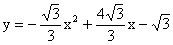
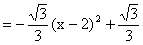
 顶点
顶点 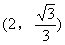 ……7分 这个点在
……7分 这个点在  的内心位置 ……8分
的内心位置 ……8分
(答外心、重心、垂心均可)
 18、解:(1)过M点作 18、解:(1)过M点作  ,垂足为N,连结MA
,垂足为N,连结MA
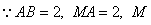 为圆心
为圆心 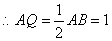
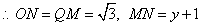
在 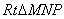 中,
中, 
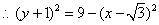
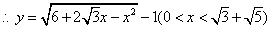
(2)当 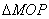 为等腰三角形时
为等腰三角形时
①若 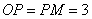 时,
时, 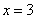
②若 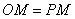 时,
时, 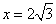
③若  时,有
时,有  即
即 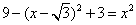
解得 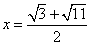 或
或 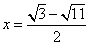 (舍去)
(舍去)
(3)当 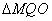 ∽
∽ 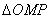 时,有
时,有  即
即 

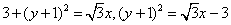
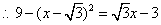
解得  或
或  (舍去) 但
(舍去) 但 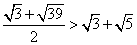
 不存在满足条件的实数
不存在满足条件的实数 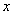 ,使
,使 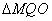 ∽
∽ 
|