|
温州市数学中考试题
卷 一
 一、选择题:(本题有12小题，每小题4分，共48分。每小题只有一个选项是正确的，不选、错选、多选均不给分)
1、计算：－1＋(＋3)的结果是( )
A、－1 B、1 C、2 D、3
2、若 eq \f(a,b)＝\f(3,5) ，则 eq \f(a＋b,b)的值是( )
A、 eq \f(8,5) B、 eq \f(3,5) C、 eq \f(3,2) D、 eq \f(5,8)
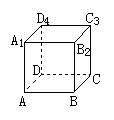
3、如图，正方体ABCD－A1B1C1D1中，与平面A1C1平行的平面是( )
A、平面AB1 B、平面AC C、平面A1D D、平面C1D
4、不等式组 eq \b\lc\{(\a\al(x－2≤0,x＋1＞0)) 的解是( )
A、x≤2 B、x≥2 C、－1＜x≤2 D、x＞－1
5、下列图形中，既是轴对称图形又是中心对称图形的是( )
6、已知抛物线的解析式为y＝(x－2)2＋1，则抛物线的顶点坐标是( )
A、(－2,1) B、(2，1) C、(2，－1) D、(1，2)
7、在一个暗箱里放入除颜色外其它都相同的3个红球和11个黄球，搅拌均匀后随机任取一个球，取到是红球的概率是( )
A、 eq \f(3,11) B、 eq \f(8,11) C、 eq \f(11,14) D、 eq \f(3,14)
8、如图，圆锥的母线长为5cm，高线长是4cm，则圆锥的底面积是( )cm2
A、3π B、9π C、16π D、25π
 9、已知x1、x2是方程x2－3x＋1＝0的两个实数根，则 eq \f(1,x1)＋\f(1,x2) 的值是( )
A、3 B、－3 C、 eq \f(1,3) D、1
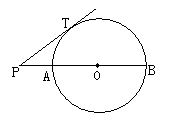
10、如图，PT切⊙O于点T，经过圆心O的割线PAB交⊙O于点A、B，已知PT＝4，PA＝2，则⊙O的直径AB等于( )
A、3 B、4 C、6 D、8
11、用换元法解方程(x2＋x)2＋(x2＋x)＝6时，假如设x2＋x＝y，那么原方程可变形为( )
A、y2＋y－6＝0 B、y2－y－6＝0 C、y2－y＋6＝0 D、y2＋y＋6＝0
12、两圆的半径分别是2cm和3cm，它们的圆心距为5cm，则这两圆的位置关系是( )
A、相离 B、外切 C、相交 D、内切
卷 二
二、填空题:(本题有6小题，每小题5分，共30分)
13、计算：2xy＋3xy＝_________。
14、已知反比例函数y＝ eq \f(k,x) 的图象经过点(1，2)，则k的值是_________。
15、在实数范围内分解因式：ab2－2a＝_________.
16、若二次函数y＝x2－4x＋c的图象与x轴没有交点，其中c为整数，则c＝_________.(只要求写出一个)
17、杉杉打火机厂生产某种型号的打火机，每只的成本为2元，毛利率为25%。工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，则这种打火机每只的成本降低了_________元.(精确到0.01元。毛利率＝ eq \f(售价－成本,成本)×100% )
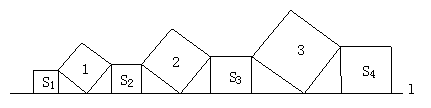
18、在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1＋S2＋S3＋S4＝_______。
三、解答题:(本题有7小题，共72分)
19、(本题8分)计算： eq \r(12)＋\f(1,2－\r(3))－(2＋\r(3))2 ;
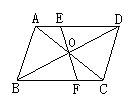
20、(本题8分)如图，四边形ABCD是平行四边形，对角线AC、BD交于点O，过点O画直线EF分别交AD、BC于点E、F。求证：OE＝OF.
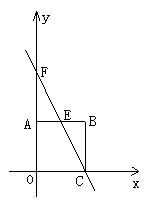
21、(本题8分)如图，在平面直角坐标系中，正方形AOCB的边长为6，O为坐标原点，边OC在x轴的正半轴上，边OA在y轴的正半轴上，E是边AB上的一点，直线EC交y轴于F，且S△FAE∶S四边形AOCE＝1∶3。
⑴求出点E的坐标；⑵求直线EC的函数解析式.
22、(本题10分)小明家用瓷砖装修卫生间，还有一块墙角面未完工(如图甲所示)，他想在现有的六块瓷砖余料中(如图乙所示)挑选2块或3块余料进行铺设，请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图，并标出所选用每块余料的编号)。
23、(本题12分)某校初三⑵班课题研究小组对本校初三段全体同学的体育达标(体育成绩60分以上，含60分)情况进行调查，他们对本班50名同学的体育达标情况和其余班级同学的体育达标情况分别进行调查，数据统计如下：
根据以上统计图，请解答下面问题：
⑴初三⑵班同学体育达标率和初三段其余班级同学达标率各是多少？
⑵假如全段同学的体育达标率不低于90%，则全段同学人数不超过多少人？
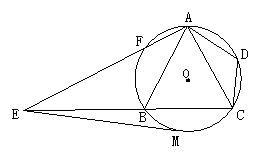
24、(本题12分)如图，已知四边形ABCD内接于⊙O，A是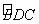 
的中点，AE⊥AC于A，与⊙O及CB的延长线分别交于点F、E，且 
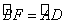，EM切⊙O于M。
⑴ △ADC∽△EBA；
⑵ AC2＝ eq \f(1,2) BC·CE；
⑶ 假如AB＝2，EM＝3，求cot∠CAD的值。
25、(本题14分)如图，在Rt△ABC中，已知AB＝BC＝CA＝4cm，AD⊥BC于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点P沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x(s)。
⑴ 求x为何值时，PQ⊥AC；
⑵ 设△PQD的面积为y(cm2)，当0＜x＜2时，求y与x的函数关系式；
⑶ 当0＜x＜2时，求证：AD平分△PQD的面积；
⑷ 探索以PQ为直径的圆与AC的位置关系。请写出相应位置关系的x的取值范围(不要求写出过程)
参考答案
一、选择题
1、C 2、A 3、B 4、C 5、B 6、B 7、D 8、B 9、A 10、C 11、A 12、B
二、填空题
13、5xy 14、2 15、a(b＋ eq \r(2))(b－ eq \r(2)) 16、略(答案不惟一)
17、0.21
18、4
三、解答题
19、解：原式＝2 eq \r(3)＋(2＋ eq \r(3))－1＝3 eq \r(3)＋1
20、证实：∵四边形ABCD是平行四边形，
∴AD∥BC，AO＝CO，
∴∠EAO＝∠FCO，
∵∠AOE＝∠COF，
∴△AOE≌△COF
∴OE＝OF
21、解：⑴∵S△FAE∶S四边形AOCE＝1∶3，
∴S△FAE∶S△FOC＝1∶4，
∵四边形AOCB是正方形，
∴AB∥OC，
∴△FAE∽△FOC，
∴AE∶OC＝1∶2，
∵OA＝OC＝6，
∴AE＝3，
∴点E的坐标是(3,6)
⑵设直线EC的解析式是y＝kx＋b，
∵直线y＝kx＋b过E(3,6)和C(6，0)
∴ eq \b\lc\{(\a\al(3k＋b＝6,6k＋b＝0)) ，解得： eq \b\lc\{(\a\al(k＝－2,b＝12))
∴直线EC的解析式是y＝－2x＋12
22、
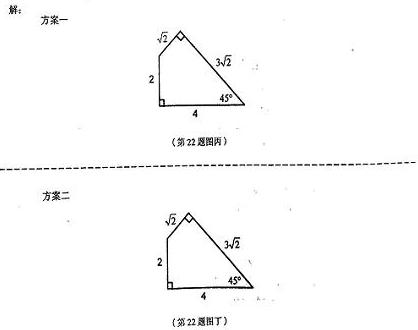
列举以下四种铺设的示意图供参考
23、解：
⑴ 初三⑵班体育成绩达标率为(1－0.02)×100%＝98%
其余班级体育成绩达标率为1－12.5%＝87.5%
答：初三⑵班体育成绩达标率和其余班级体育成绩达标率分别为98%和87.5%
⑵、设全校有x名同学，由题意得：
50×98%＋(x－50)×87.5%≥90%，
解得：x≤210
答：全段同学人数不超过210人。①
24、解：
⑴∵四边形ABCD内接于⊙O，∴∠CDA＝∠ABE，
∵
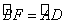，∴∠DCA＝∠BAE，
∴△CAD∽△AEB
⑵、过A作AH⊥BC于H(如图)
∵A是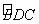
中点，∴HC＝HB＝ eq \f(1,2) BC，
∵∠CAE＝900，∴AC2＝CH·CE＝ eq \f(1,2) BC·CE
⑶∵A是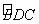
中点，AB＝2，∴AC＝AB＝2，
∵EM是⊙O的切线，∴EB·EC＝EM2 ①
∵AC2＝ eq \f(1,2) BC·CE，BC·CE＝8 ②
①＋②得：EC(EB＋BC)＝17，∴EC2＝17
∵EC2＝AC2＋AE2，∴AE＝ eq \r(17－22)＝\r(13)
∵△CAD∽△ABE，∴∠CAD＝∠AEC，
∴cot∠CAD＝cot∠AEC＝ eq \f(AE,AC)＝\f(\r(13),2)
25、解：
⑴∵当Q在AB上时，显然PQ不垂直于AC。
当，由题意得：BP＝x，CQ＝2x，PC＝4－x，
∴AB＝BC＝CA＝4，∠C＝600，
若PQ⊥AC，则有∠QPC＝300，∴PC＝2CQ
∴4－x＝2×2x，∴x＝ eq \f(4,5) ，
∴当x＝ eq \f(4,5) (Q在AC上)时，PQ⊥AC；
⑵ 当0＜x＜2时，P在BD上，Q在AC上，过点Q作QH⊥BC于H，
∵∠C＝600，QC＝2x，∴QH＝QC×sin600＝ eq \r(3)x
∵AB＝AC，AD⊥BC，∴BD＝CD＝ eq \f(1,2) BC＝2
∴DP＝2－x，∴y＝ eq \f(1,2) PD·QH＝ eq \f(1,2) (2－x)· eq \r(3)x＝－ eq \f(\r(3),2)x2＋\r(3)x
⑶ 当0＜x＜2时，在Rt△QHC中，QC＝2x，∠C＝600，
∴HC＝x，∴BP＝HC
∵BD＝CD，∴DP＝DH，
∵AD⊥BC，QH⊥BC，∴AD∥QH，
∴OP＝OQ
∴S△PDO＝S△DQO，
∴AD平分△PQD的面积；
⑷ 显然，不存在x的值，使得以PQ为直径的圆与AC相离
当x＝ eq \f(4,5)或 eq \f(16,5)时，以PQ为直径的圆与AC相切。
当0≤x＜ eq \f(4,5)或 eq \f(4,5)＜x＜ eq \f(16,5)或 eq \f(16,5)＜x≤4时，以PQ为直径的圆与AC相交。
|
