| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
一、填空题:(本题共12小题,每小题3分,满分36分) 1. 计算: 2. 上海已进入老龄化城市,预计到2025年,上海65岁及以上老人将达到 400万人,“400万”用科学记数法可表示为_________. 3. 函数 4. 若 5. 不等式组 6. 抛物线 7. 在△ 8. 若分式 9. 若两圆外切,则它们的公切线共有 条. 10. 已知菱形的周长40cm,一条对角线长12 cm,则另一条对角线的长为______ cm. 11. 2005年某市人均GDP约为2003年的1.21倍,假如该市每年的人均GDP增长率相同,那么该增长率为 . 12. 旋转180°得到△ 则△ 二、选择题:(本题共4小题,每小题4分,满分16分) 13.在统计中,样本的标准差可以反映这组数据的 …………………( ). (A)平均状态; (B)分布规律; (C)离散程度; (D)数值大小. 14.下列各式中,在实数范围内不能分解因式的是 …………………( ). (A) 15. 下列四边形中,对角线一定相等是 ………………………………( ). (A)菱形和矩形 ; (B)矩形和等腰梯形; (C)平行四边形和等腰梯形; (D)菱形和直角梯形. 16. 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为5cm,若这两个三角形相似,则△DEF的另两边长是下列各组中的 …………………………………………………………………( ). (A)2 cm,3 cm;(B)4 cm,6 cm;(C)6 cm,7 cm;(D)7 cm,9 cm. 三、(本题共5小题,17、18小题每题9分,19~21小题每题10分,满分48分) 17.先化简,后求值: 18.解方程组:
(1) 点B坐标为_________ . (2) 若将△ABC沿 △ABC绕原点O旋转180°得到 △A2B2C2,则点B2的坐标为_________,△A1B1C1与△A2B2C2关于_________轴对称. (3) 若△ABC与△EFD成中心对称,则对 称中心的坐标为_________. 20.在直角坐标平面内,把过原点的直线l与双曲线: (1)求直线l的函数解析式; (2)将直线l向上平移4个单位后,直线l与 21.某初级中学四个年级学生人数分布如图(a),通过对全体学生寒假期间所读课外书情况调查,制成各年级读课外书情况的条形图,如图(b),已知该校被调查的四个年级共有学生1200人,则 (1)预备年级学生占四个年级总人数的________%; (2)寒假期间人均读课外书最少的是________年级学生,读课外书总量最少的是________年级学生;
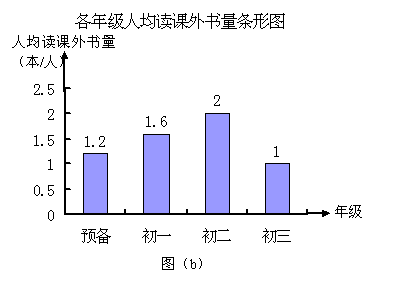
四、(本题共4小题,22~24小题每题12分,25小题14分,满分50分)
(1)求 (2)当建设费用为6万元时,求被利用的旧墙的长度为多少米? 23.如图△ABC,△CDE都是等边三角形,且点B、C、D在同一直线上,连结AD交CE于点F,连结BE交AC于点G,AD、BE相交于点M,
(2)在不添加新的字母和线段的前提下,在图 中再找出2个与△ABG相似的三角形.
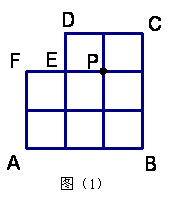 24. 将8个边长为1的正方形拼成如图(1)外形,要求过点P作一条直线l将该图形分割成面积相等的两部分, 24. 将8个边长为1的正方形拼成如图(1)外形,要求过点P作一条直线l将该图形分割成面积相等的两部分,
(1)在图(1)中画出直线l的大致位置; (2)计算直线l与直线AB所成的夹角(锐角)的正切值.
25.抛物线 (1)求证:A、B两点都在 (2)已知圆P(点P在第一象限)过A、B两点,且与 ①求圆心P点的坐标;(用含有 ②当
2006年卢湾区初三模拟考试参考答案 一、 填空题:(本题共12小题,每小题3分,满分36分) 1. 7.15; 8.3; 9. 3; 10.16; 11. 10%; 12. 6. 二、选择题:(本题共4小题,每小题4分,满分16分) 13.C; 14.C; 15.B; 16.B. 三、(本题共5小题,17、18小题每题9分,19~21小题每题10分,满分48分) 17. 解:原式= = = 把 18.解1: 代入(1)得 解得 代入(3)解得 方程组的解为 解2:由(1)得 与(2)组成 解得 19. (1)(1,1);(2)(-1,1),(-1-1), (每空2分) 20.解:将 设直线l的函数解析式为 将 直线l的函数解析式为 将直线l向上平移4个单位后,直线l的解析式为 可得B
21.(1)20;(2)初三,预备;(3)1.44. 第(1)、(3)小题每题3分,第(2)小题4分. 四、(本题共4小题,22~24小题每题12分,25小题14分,满分50分) 22. 解:另一边的长度为
(2)由题意得
化简得 解得 经检验 答:(略) 23.(1)证实:∵△ABC,△CDE都是等边三角形, ∴∠ACB=∠ECD=60°,∴∠ACB ∠GCF=∠FCD ∠GCF, 即∠BCE=∠ACD,……………………………………………………2分 又∵BC=AC,CE=CD,∴△BCE≌△ACD, ………………………2分 ∴∠BEC=∠ADC,∵∠ABC=∠ECD=60°,∴AB∥CE,…………2分 ∴∠ABE=∠BEC,∴∠ABE=∠ADC,………………………………1分 又∵∠BAC=∠CED=60°,∴△ABG∽△CDF.……………………1分 (2)写出△BDA,△MEF,△MBA,△CEG中的任意2个.……4分 24. 解:(1)草图正确 ……………………………………………3分 (2) 设CM=x,由CD∥AB,得 解得 由梯形NBCM的面积为4,得 解得 作MH⊥AB,垂足为H,
设CG= x,由CD∥AB 得 解得
由梯形NBCM的面积为4,得 解得
25. 解:(1)由抛物线
设A (2)①如图,过P点作PH⊥AB,垂足为H, 由垂径定理得点H是AB中点,因此圆心P必在抛物线的对称轴上, 设P 连结AP,在Rt△AHP中, 即 ∴圆心P点的坐标为P ②当 1°若两圆外切, Q的坐标为 2°若两圆内切, Q的坐标为 综上所述满足条件的圆的圆心Q的坐标为
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |