| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
现经市场调查发现,在一个月中(按30天记数)有20天可卖出150份/天,有10天只能卖出100份/天,而报社规定天天批发给摊点的报纸的数量必须相同. (1)通过在坐标系中(以退还的钱数为纵坐标,退还的报纸数量为横坐标)描出点,分析出退还的钱数y(元)与退还的报纸数量k(份)之间的函数关系式. (2)若该家报刊摊点天天从报社买进的报纸数x份(满足100<x<150),则当买进多少报纸时,毛利润最大?最多可赚多少钱? 27、(本题满分8分)
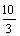
 在一块长16m、宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案. 在一块长16m、宽12m的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半. 下面分别是小明和小颖的设计方案.
小明说:我的设计方案如图(1),其中花园四面小路的宽度相等. 通过解方程,我得到小路的宽为2m或12m. 小颖说:我的设计方案如图(2),其中花园中每个角上的扇形相同. (1)你认为小明的结果对吗?请说明理由. (2)请你帮助小颖求出图中的x(精确到0.1m).
四、解答题(本大题共有2小题,共18分.) 28、(本题满分8分) 如图,在△ABC中,∠C=90°,AC=6,BC=8,M是BC的中点,P为AB上的一个动点,(可以与A、B重合),并作∠MPD=90°,PD交BC(或BC的延长线)于点D. (1)记BP的长为x,△BPM的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围; (2)是否存在这样的点P,使得△MPD与△ABC相似?若存在,请求出x的值;若不存在,请说明理由.
 29、(本题满分10分) 29、(本题满分10分)
如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是ABC的中点,弦DE⊥AB,垂足为F,DE交AC于点G. (1)图中有哪些相等的线段?(要求:不再标注其他字母,找结论的过程中所作的辅助线不能出现在结论中,不写出推理过程) (2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证实;若不成立,请说明理由.
参考答案 一、细心填一填 1. ﹣ 二、精心选一选 13. C 14. B 15. A 16. C 17. D 18. C 19. D 20. C 三、认真答一答 21. (1)3;(2)a=4 ; (3) 2x-1 ,3 22. 略 23.(1) ①②⑤ 证实:在AB上取点M,使AM=AD,连结EM,可证△AEM≌△AED, △BEM≌△BCE,∴∠D=∠AME, ∠C=∠BME,故∠D ∠C=∠AME ∠BME=180° ∴AD∥BC. (2)①②③ △ABM中,E是内心,过E作DC⊥EM,显然有,AE平分∠BAM,BE平分∠ABM,ED=EC,但AD不平分于BC. 24.(1)0元的频数是5,2元的频数是7,5元的频数是21,6元的频数是5,8元的频数是2. (2)平均数是4.125,中位数是5,众数是5. (3)5元. 25.(1) 26.(1)通过作图,知y=mk n, 当0<k<30,且为整数, y=﹣0.1k 0.3;当k≥30 , y=0.02. (2) S=2×0.2x+100×10×0.2-(0.3-y)(x-100)= 4x+200-0.1(x-100) =﹣0.1x+24x-800. 当x=﹣ 27.(1)设小路的宽为xm,则(16-2x)(12-2x)= (2)四个角上的四个扇形可合并成一个圆,设这个圆的半径为rm,
(3)依此连结各边的中点得如图的设计方案. 28.(1)作PK⊥BC于K,BM=4,AB=10,∵PK∥AC,∴ ∴y= (2)①∠PMB=∠B, PM=PB ,MK=KB=2 , ②∠PMD=∠A, 又∠B =∠B,∴△BPM∽△BAC, ∴BP·AB=BM·BC, ∴10x=4×8 ,x=3.2,∴存在 x=2.5或3.2. 29.(本题仅供学有余力的同学参考)(1)OA=OB,DF=EF,DE=AC,AG=DG,EG=CG. (2)ME=GM. 理由是:连EO并延长交⊙O于点N,连结DN. ∵EM是⊙O的切线,∴∠OEM=90º,∴∠GEM ∠GEN=90º. ∵EN是⊙O的直径,∠N ∠GEN=90º, ∴∠N=∠GEM. ∵AB是⊙O的直径,∴∠B ∠BAC=90º,∵∠AGF ∠GAF=90º,∴∠AGF=∠B,∵∠AGF=∠CGE,∴∠CGE=∠B. ∵AC=DE,∴∠N=∠B,∴∠GEM=∠CGE,∴MG=ME. (3)答案: |
|||||||||||||||||||||||||||||||||||||||
| |