中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
| 得 分
| 评卷人
|
| |
|
(第1题图) |
一、填空题（本大题共15小题，每小题2分，满分30分）
1. 亲爱的同学们，在我们的生活中处处有数学的身影.请看图，
折叠一张三角形纸片，把三角形的三个角拼在一起，就得到
一个闻名的几何定理，请你写出这一定理的结论：“三角形
的三个内角和等于_______°.”
2. 按照神舟号飞船环境控制与生命保障分系统的设计指标，“神舟”五号飞船返回舱的温度为21℃±4℃.该返回舱的最高温度为________℃.
3. 点A(-2,1)在第_______象限.
4. 分解因式:a2-1=_______.
5. 不等式组 
6. 已知等腰三角形的一边等于5,另一边等于6,则它的周长等于_______.
7. 已知方程 
8.
|
A |
|
D |
|
B |
|
C |
|
(第11题图) |
用48米长的竹篱笆在空地上,围成一个绿化场地,现有两种设计方案,一种是围成正方形的场地;另一种是围成圆形场地.现请你选择,围成
________(圆形、正方形两者选一)场在面积较大.
9. 已知数据x1，x2，…，xn的平均数是 
数据x1 8,x2 8,…,xn 8的平均数是____.
|
A |
|
B |
|
10m |
|
8m |
10. 在直角三角形ABC中，∠C=90°，已知sinA= 
则cosB=_______.
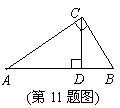
11. 如图，已知CD是Rt△ABC的斜边上的高，其中
AD=9cm，BD=4cm，那么CD等于_______cm.
12. 二次函数y=x2-2x 1的对称轴方程是x=_______.
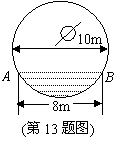
13. 在直径为10m的圆柱形油槽内装入一些油后，截
面如图所示，假如油面宽AB=8m，那么油的最大
深度是______m.
14. 等腰梯形是__________对称图形.
15. 对甲、乙两台机床生产的零件进行抽样测量，其平均数、方差计算结果如下：
机床甲： 
得 分
评卷人
二、单项选择题（本大题共10小题，每小题3分，满分30分）
16. 下列四个实数中是无理数的是 ( ).
A.2.5 B. 
17. 一个容量为50的样本,在整理频率分布时,将所有频率相加,其和是( ).
A.50 B.0.02 C.0.1 D.1
18. 假如t>0,那么a t与a的大小关系是 ( ).
|
(第19题图) |
|
③ |
|
① |
|
② |
A.a t>a B.a t<a C.a t≥a D.不能确定
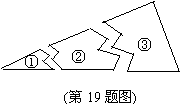
19. 如图,某同学把一块三角形的玻璃打坏成三片,现在他
要到玻璃店去配一块完全一样外形的玻璃.那么最省
事的办法是带________去配. ( ).
A.① B.② C.③ D.①和②
20. 数据”1,2,1,3,1”的众数是 ( ).
A.1 B.1.5 C.1.6 D.3
21. 在银行存款预备金不变的情况下,银行的可贷款总量与存款预备金率成反比例关系.当存款预备金率为7.5%时,某银行可贷款总量为400亿元,假如存款预备金率上调到8%时,该银行可贷款总量将减少________亿. ( ).
A.20 B.25
C.30 D.35
22. 假如两圆只有两条公切线,那么这两圆的位置关系是 ( ).
A.内切 B.外切
C.相交 D.外离
23. 一个多边形的每一个外角都等于72°,这个多边形是 ( ).
A.正三角形 B.正方形
C.正五边形 D.正六边形
24. 小明在一次登山活动中捡到一块矿石,回家后,他使用一把刻度尺,一只圆柱形的玻璃杯和足量的水,就测量出这块矿石的体积.假如他量出玻璃杯的内直径d,把矿石完全浸没在水中,测出杯中水面上升了高度h,则小明的这块矿石体积是 ( ).
A. 
C. 
25. 分式 
A.x=-3 B.x=3
C.x=-3或x=1 D.x=3或x=-1
得 分
评卷人
三、解答题（本大题共3小题,每小题5分，满分15分）
26. 计算: 
|
|
27. 解方程组 
28. 在△ABC中,∠A,∠B都是锐角,且sinA= 
得 分
评卷人
四、（本大题共2小题,第29题8分,第30题9分,共17分）
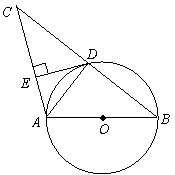
29. 如图,AB是⊙O的直径, ⊙O过BC的中点D,DE⊥AC.求证: △BDA∽△CED.
|
B |
A |
|
C |
|
D |
|
E |
|
O |
 |
30. 某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元：
① 求出y与x的函数关系式.(纯利润=总收入-总支出)
② 当y=106000时,求该厂在这个月中生产产品的件数.
得 分
评卷人
五、（本大题满分8分）
31．小王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接
下来的一周交易日内，小王记下该股票每日收盘价格相比前一天的涨跌情况：
（单位：元）
星期
一
二
三
四
五
每股涨跌（元）
2
-0.5
1.5
-1.8
0.8
根据上表回答问题：
① 星期二收盘时，该股票每股多少元？（2分）
② 周内该股票收盘时的最高价，最低价分别是多少？（4分）
③ 已知买入股票与卖出股票均需支付成交金额的千分之五的交易费。若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？（2分）
2004年芜湖市高中招生考试
数学加试试卷
注重：1.数学试卷分两部分，第一部分4页，共31题；第二部分为加试试卷4页，共8题；总共8页，共39题。报考各类高中的考生全做；只参加毕业考试的考生无加试试卷。请您仔细核对每页试卷下页码和题数，核实无误后再答题.
2.请你仔细思考、认真答题，不要过于紧张，祝考试顺利！
题 号
六
七
八
九
总 分
得 分
得 分
评卷人
六、填空题（本大题满分20分，每小题4分）
32. 某商场在促销期间规定：商场内所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，按如下方案获得相应金额的奖券.（奖券购物不再享受优惠）
消费金额x的范围（元）
200≤x<400
400≤x<500
500≤x<700
…
获得奖券的金额（元）
30
60
100
…
根据上述促销方法，顾客在该商场购物可获得双重优惠，假如胡老师在该商场购标价450元的商品，他获得的优惠额为_________元.
33. 如图,正方形ABCD内接于⊙O,E为DC的中点,直线BE交⊙O于点F,假如⊙O的半径为 
|
A |
B |
|
C |
|
D |
|
E |
O |
|
F |
|
M |
（第33题图） |
（第35题图） |
O |
 | |||
 | |||
34. 关于x的方程m2x2 (2m 3)x 1=0有两个乘积为1的实数根,方程x2 (2a m)x 2a 1-m2=0有一个大于0且小于4的实数根,则a的整数值是_________.
35. 如图,正六边形与正十二边形内接于同一圆⊙O中,已知外接圆的半径为2,则阴影部分面积为_________.
36. 按照一定顺序排列的一列数叫数列,一般用a1，a2，a3，…，an表示一个数列，可简记为{an}.现有数列{an}满足一个关系式：an 1= 
得 分
评卷人
七、（本大题满分8分）
37. 通过市场调查，一段时间内某地区特种农产品的需求量y（千克）与市场价格x（元/千克）存在下列函数关系式：y= 
（1） 根据以上市场调查，请你分析当市场处于平衡状态时，该地区这种农产品的市场价格与这段时间内农民的总销售收入各是多少？（4分）
（2） 受国家“三农”政策支持，该地区农民运用高科技改造传统生产方式，减少产量，以大力提高产品质量.此时生产数量z与市场价格x的函数关系发生改变，而需求函数关系未发生变化，当市场再次处于平衡状态时，市场价格已上涨了a(0<a<25)元，问在此后的相同时间段内该地区农民的总销售收入是增加了还是减少了？变化多少？（4分）
得 分
评卷人
八、（本大题满分10分）
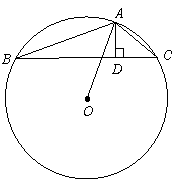
38.在钝角△ABC 中，AD⊥BC,垂足为D点，且AD与DC的长度为x2-7x 12=0方程的两个根，⊙O是△ABC的外接圆，假如BD长为a(a>0).
求△ABC的外接圆⊙O的面积.
|
A |
B |
|
C |
|
D |
|
O |
 |
得 分
评卷人
九、（本大题满分12分）
39. 如图①，在平面直角坐标系中，AB、CD都垂直于x轴，垂足分别为B、D且AD与B相交于E点.已知：A(-2,-6),C(1,-3)
(1) 求证：E点在y轴上；（4分）
(2) 假如有一抛物线经过A，E，C三点，求此抛物线方程.（4分）
(3) 假如AB位置不变，再将DC水平向右移动k(k>0)个单位，此时AD与BC相交于E′点，如图②，求△AE′C的面积S关于k的函数解析式.（4分）
|
C（1，-3） |
|
A （2，-6） |
|
B |
|
D |
|
O |
|
x |
|
E |
|
y |
|
（第39题图②） |
|
C（1 k，-3） |
|
A （2，-6） |
|
B |
|
D |
|
O |
|
x |
|
E′ |
|
y |
 | |||
 | |||
|
2004年芜湖市初中毕业、高中招生考试
数学试卷参考答案及评分标准
一、填空题（本大题共15小题，每题2分，满分30分）
1. 180 2. 25 3. 二 4. (a 1)( a-1) 5. x>2 6. 16或17 7. 6 8. 圆形
9. 
二、单项选择题（本大题共10小题，每题3分，满分30分）
题号
16
17
18
19
20
21
22
23
24
25
答案
C
D
A
C
A
C
C
A
A
三、（本大题共3小题，每题5分，满分15分）
|
26.解：原式=4-8×0.125 1 1
|
=4-1 2
|
=5
|
27.解：① 2×②得：7x=21
|
x=3
|
把x=3代入②得y=-2
|
A |
|
B |
|
C |
|
∴原方程组的解是 
|
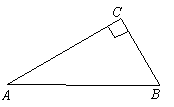
28.解：由已知可得：∠A=30°，∠B=60°
|
∴△ABC为Rt△，且∠C=90°
又AB=10，∴BC=AB·sin30°=10 
|
AC=AB·cos30°=10 
|
∴S△ABC= 
四、（本大题共2小题，每29题8分，第30题9分，共17分）
|
|
29.证法一：∵AB是⊙O直径
∴AD⊥BC
|
又BD=CD
∴AB=AC
|
∴∠B=∠C
|
又∠ADB=∠DEC=90°
|
|
∴△BDA∽△CED
证法二：连结DO，∵BO=OA
BD=DC
|
∴DO∥CA
∴∠BDO=∠C
又∠BDO=∠B
|
∴∠B=∠C
∵AB是直径，DE⊥AC
∴∠ADB=∠DEC=90°
|
∴△BDA∽△CED
|
30．解：①依题意得：y=80x-60x-0.5x·2-8000
|
y=19x-8000
|
∴所求的函数关系式为y=19x-8000(x>0且x是整数)
（x取值范围不写不扣分）
|
②当y=106000时，代入得：
|
106000=19x-8000
|
19x=114000
|
x=6000
∴这个月该厂生产产品6000件.
五、（本大题满分8分）
|
|
31．解：（1）星期二收盘价为25 2-0.5=26.5（元/股）
|
（2）收盘最高价为25 2-0.5 1.5=28(元/股)
|
收盘最低价为25 2-0.5 1.5-1.8=26.2（元/股）
（3）小王的收益为：27×1000(1-5‰)-25×1000（1 5‰）
=27000-135-25000-125
=1740（元）
|
∴小王的本次收益为1740元.
2004 年 芜 湖 市 高 中 招 生 考 试
数学加试试卷参考答案及评分标准
六、填空题（本大题满分20分，每小题4分）
32.120 33. 
七、（本大题满分8分）
|
|
37.解：（1）由已知市场处于平衡，此时y=z得 
|
（x-25）(x 10)=0, ∴x1=25,x2=-10(舍去)
|
把x=25代入z=400x中，得z=10000（千克）
一段时间内该地区农民的总销售收入=25×10000=250000（元）
（2）∵需求函数关系未变，∴平衡点仍在需求函数图象上.
由已知此时价格为(a 25)元/千克，代入 
|
得：此时的需求数量 
又∵此时市场处于平衡，生产数量z1=需求数量y1,
∴此时的总销售收入为：
|
|
(a 25)· 
∴农民总销售收入增加了(250000 6000a)-250000=6000a(元)
八、
|
A |
B |
|
C |
|
D |
|
O |
|
E |
（本大题10分）
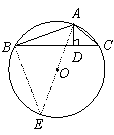
38.解：∵AD与DC的长度为x2-7x 12的两根
|
∴有两种情况：①AD=3，DC=4
②AD=4，DC=3
|
由勾股定理：求得AC=5
（求△ABC的外接圆⊙O的直径长，
介绍三种方法供参考）
|
方法一：连接AO并延长交⊙O于E点，连接BE
|
|
∴∠ABE=90°
又∵∠E=∠C
|
|
∴△ABE∽△ADC，∴
方法二：连接AO并延长交⊙O于E点，连接BE
|
∴∠ABE=90°
在Rt△ADC中：sinC= 
|
又∵∠C=∠E，∴sinC=sinE
|
∴
|
方法三：在Rt△ADC中，sinC=
由正弦定理： 
|
可得： 
① 
|
当AD=3，DC=4时， 
|
⊙O的面积为： 
② 
|
当AD=4，DC=3时， 
|
⊙O的面积为： 
<注>(结果有两种情况，只求出一种正确结果，只能得8分)
九、（本大题满分12分）
39．解：（1）（本小题介绍二种方法，供参考）
方法一：过E作EO′⊥x轴，垂足O′∴AB∥EO′∥DC
|
∴ 
又∵DO′ BO′=DB
|
∴ 
∵AB=6，DC=3，∴EO′=2
|
又∵ 
|
∴DO′=DO，即O′与O重合，E在y轴上
|
方法二：由D（1，0），A（-2，-6），得DA直线方程：y=2x-2①
|
再由B（-2，0），C（1，-3），得BC直线方程：y=-x-2 ②
|
联立①②得 
|
∴E点坐标（0，-2），即E点在y轴上
（2）设抛物线的方程y=ax2 bx c(a≠0)过A（-2，-6），C（1，-3）
|
|
|
E（0，-2）三点，得方程组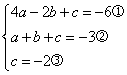 
解得a=-1,b=0,c=-2
|
|
∴抛物线方程y=-x2-2
(注：题目未告之E（0，-2）是抛物线的顶点，如设顶点式求解正确只能得6分)
（3）（本小题给出三种方法，供参考）
由（1）当DC水平向右平移k后，过AD与BC的交点E′作E′F⊥x轴垂足为F。
|
同（1）可得：
|
方法一：又∵E′F∥AB 
|
S△AE′C= S△ADC- S△E′DC= 
= 
|
S=3 k为所求函数解析式
|
方法二：∵ BA∥DC，∴S△BCA=S△BDA
|
∴S△AE′C= S△BDE′ 
|
∴S=3 k为所求函数解析式.
|
证法三：S△DE′C∶S△AE′C=DE′∶AE′=DC∶AB=1∶2
|
同理：S△DE′C∶S△DE′B=1∶2,又∵S△DE′C∶S△ABE′=DC2∶AB2=1∶4
|
∴ 
|
∴S=3 k为所求函数解析式.
| |
