|
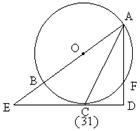
1、如图,已知AB是⊙O的直径,过⊙O上的点C的切线交AB的延长线于E,AD⊥EC于D且交⊙O于F。
⑴求证:AD DF=AB;⑵若CE= 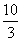 ,EB=
,EB= 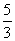 ,求⊿ADE的面积。
,求⊿ADE的面积。
2、已知P是∠XAY的平分线上的一点,过A、P两点任作一圆,若此圆交∠XAY的两边于B、C。求证:AB AC为一定值。
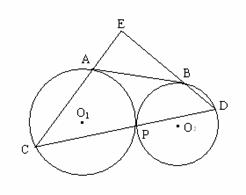
3、如图,已知⊙O1和⊙O2外切于P点,AB是两圆的外公切线,A、B为切点,过点P的直线交⊙O1于点C,交⊙O2于点D,分别延长CA、DB相交于点E,求证:CE⊥DE
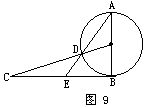 4、如图9,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E. 4、如图9,已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E.
(2)取BE的中点F,连结DF.求证:DF是⊙O的切线;
(3)过点D作DG⊥BC,垂足为G,OE与DG相交于点M.
①求证:DM=GM;
②连结BM并延长,与OC相交于点N.试判定以N为圆心,经过点E的⊙N与⊙O的位置关系,并说明理由.
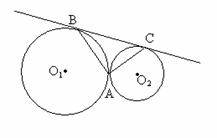
5、已知:⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为
切点。求证:AB⊥AC
6、AB为⊙O直径,BC切⊙O于B,BC=AB,AC交⊙O于点D,CO交BD于点M,过M作EF⊥AB于E,交AC于F。求证:(1)BM=2DM。
(2)AD·DF=DM  EM·FM
EM·FM
7、已知:如图,AB是⊙O的直径,AB交弦CD于M(M与O不重合),且M是CD的中点,P是CD延长线上一点,PE切⊙O于E,AE交CD于F.
求证:(1) PF2=PC·PD;
 (2) PM2–PF2=MA·MB. (2) PM2–PF2=MA·MB.
8、⊙O与⊙O1相交于A,B,PN切⊙O于N交⊙O1于PN,M是PN的中点,延长BA交PN于Q。
(1) 求证:MQ:QN:PM:PQ=1:2:3:4
(2)
若由点Q引一直线交⊙O于F,D交⊙O1于H,E。求证: 
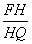 =
= 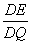 。
。
9、如图已知⊙O1与⊙O2外切,⊙O1的半径r=2cm,⊙O2的半径R=6cm,
AB、CD为外公切线。
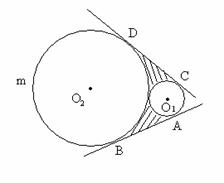 ⑴求 ⑴求  的长 的长
⑵图中阴影部分的面积
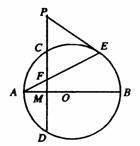
10、如图,在⊙O中,弦CD垂直于直径AB,垂足为H,弦BE与
半径OC相交于点F,且OF=FC,弦DE与弦AC相交于点G
(1) 求证:AG·BF=DG·OF;
(2) 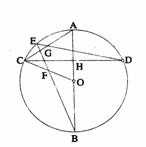 求证:AG=GC; 求证:AG=GC;
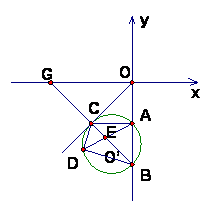
11、已知:如图10,在平面直角坐标系中,半径为 SHAPE \* MERGEFORMAT 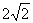 的⊙O’与y轴交于A、B两点,与直线OC相切于点C,∠BOC=45°,BC⊥OC,垂足为C.
的⊙O’与y轴交于A、B两点,与直线OC相切于点C,∠BOC=45°,BC⊥OC,垂足为C.
(1)判定△ABC的外形;
(2)在弧BC上取一点,连结DA、DB、DC,DA交BC于点E.
求证:BD·CD=AD·ED;
(3)延长BC交x轴于点G,求经过O、C、G三点的二次函数的解析式.
|