|
|
 |
| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
|
[组图]中考数学代数解答题
|
| 查询数中考复习的详细结果
|
|
中考数学代数解答题
(08北京市卷)13.(本小题满分5分)计算: 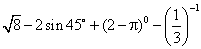 .
.
解: 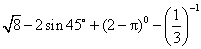
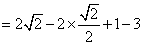 ························································································ 4分
························································································ 4分
 .·········································································································· 5分
.·········································································································· 5分
(08北京市卷)14.(本小题满分5分)
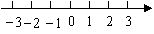 解不等式 解不等式  ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
14.(本小题满分5分)
解:去括号,得 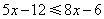 .······································································ 1分
.······································································ 1分
移项,得  .·············································································· 2分
.·············································································· 2分
合并,得  .····························································································· 3分
.····························································································· 3分
系数化为1,得  .····················································································· 4分
.····················································································· 4分
不等式的解集在数轴上表示如下:
(08北京市卷)16.(本小题满分5分)
如图,已知直线 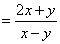 经过点
经过点 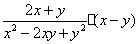 ,求此直线与
,求此直线与  轴,
轴, 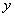 轴的交点坐标.
轴的交点坐标.
16.(本小题满分5分)
解:由图象可知,点 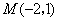 在直线
在直线 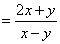 上,············································ 1分
上,············································ 1分
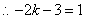 .
.
解得 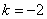 .······································································································ 2分
.······································································································ 2分
 直线的解析式为
直线的解析式为  .········································································· 3分
.········································································· 3分
令  ,可得
,可得 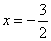 .
.
 直线与
直线与  轴的交点坐标为
轴的交点坐标为 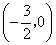 .································································· 4分
.································································· 4分
令 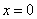 ,可得
,可得 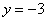 .
.
 直线与
直线与 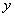 轴的交点坐标为
轴的交点坐标为 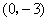 .·································································· 5分
.·································································· 5分
(08北京市卷)17.(本小题满分5分)
已知 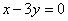 ,求
,求 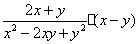 的值.
的值.
解: 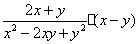
 ······························································································· 2分
······························································································· 2分
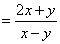 .·········································································································· 3分
.·········································································································· 3分
当 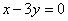 时,
时, 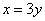 .·················································································· 4分
.·················································································· 4分
原式 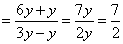 .··················································································· 5分
.··················································································· 5分
|
“限塑令”实施前,平均一次购物使用不同数量塑料购物袋的人数统计图
|
|
“限塑令”实施后,使用各种
购物袋的人数分布统计图
|
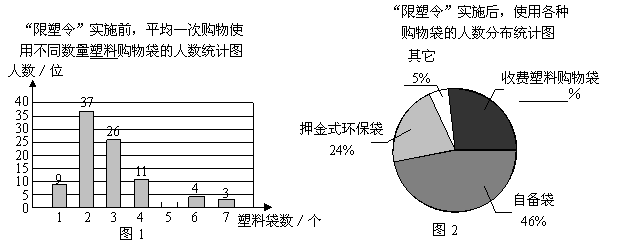 (08北京市卷)20.为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分: (08北京市卷)20.为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
|
处理方式 |
直接丢弃 |
直接做垃圾袋 |
再次购物使用 |
其它 |
|
选该项的人数占
总人数的百分比 |
5% |
35% |
49% |
11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,假如天天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市天天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.
解:(1)补全图1见下图.·················································································· 1分
|
“限塑令”实施前,平均一次购物使用不同数量塑料购物袋的人数统计图
|
 (个).
(个).
这100位顾客平均一次购物使用塑料购物袋的平均数为3个.······························ 3分
 .
.
估计这个超市天天需要为顾客提供6000个塑料购物袋.······································· 4分
(2)图2中,使用收费塑料购物袋的人数所占百分比为 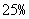 .···························· 5分
.···························· 5分
根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.····· 6分
(08北京市卷)21.(本小题满分5分)列方程或方程组解应用题:
京津城际铁路将于2008年8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.假如这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?
21.解:设这次试车时,由北京到天津的平均速度是每小时  千米,则由天津返回北京的平均速度是每小时
千米,则由天津返回北京的平均速度是每小时  千米.····················································································································· 1分
千米.····················································································································· 1分
依题意,得 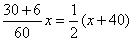 .······································································ 3分
.······································································ 3分
解得  .···································································································· 4分
.···································································································· 4分
答:这次试车时,由北京到天津的平均速度是每小时200千米.·························· 5分
(08北京市卷)23.已知:关于  的一元二次方程
的一元二次方程  .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为  ,
, 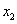 (其中
(其中 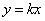 ).若
).若 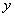 是关于
是关于  的函数,且
的函数,且 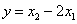 ,求这个函数的解析式;
,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量  的取值范围满足什么条件时,
的取值范围满足什么条件时,  .
.
 23.(1)证实: 23.(1)证实: 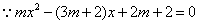 是关于
是关于  的一元二次方程,
的一元二次方程,
 .
.
 当
当 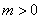 时,
时, 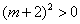 ,即
,即  .
.
 方程有两个不相等的实数根.……2分
方程有两个不相等的实数根.……2分
(2)解:由求根公式,得 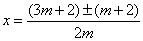 .
.
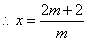 或
或 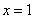 .······················································································· 3分
.······················································································· 3分
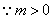 ,
,
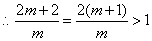 .
.
 ,
,
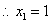 ,
, 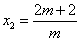 .···················································································· 4分
.···················································································· 4分
 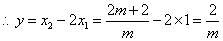 .
.
即  为所求.··················· 5分
为所求.··················· 5分
(3)解:在同一平面直角坐标系中分别画出
 与
与 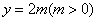 的图象.
的图象.
······························································ 6分
由图象可得,当 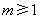 时,
时, 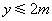 .···· 7分
.···· 7分
(08北京市卷)24.在平面直角坐标系  中,抛物线
中,抛物线 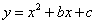 与
与  轴交于
轴交于 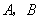 两点(点
两点(点 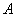 在点
在点 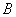 的左侧),与
的左侧),与 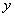 轴交于点
轴交于点  ,点
,点 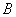 的坐标为
的坐标为 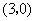 ,将直线
,将直线 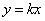 沿
沿 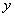 轴向上平移3个单位长度后恰好经过
轴向上平移3个单位长度后恰好经过  两点.
两点.
(1)求直线  及抛物线的解析式;
及抛物线的解析式;
(2)设抛物线的顶点为 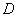 ,点
,点 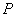 在抛物线的对称轴上,且
在抛物线的对称轴上,且  ,求点
,求点 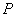 的坐标;
的坐标;
(3)连结 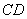 ,求
,求 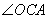 与
与 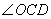 两角和的度数.
两角和的度数.
24.解:(1)  沿
沿 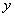 轴向上平移3个单位长度后经过
轴向上平移3个单位长度后经过 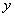 轴上的点
轴上的点  ,
,
 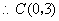 .
.
设直线  的解析式为
的解析式为  .
.
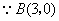 在直线
在直线  上,
上,
 .
.
解得  .
.
 直线
直线  的解析式为
的解析式为 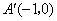 .……1分
.……1分
 抛物线
抛物线 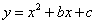 过点
过点  ,
,

解得 
 抛物线的解析式为
抛物线的解析式为 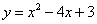 .································································· 2分
.································································· 2分
 (2)由 (2)由 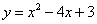 .
.
可得 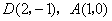 .
.
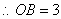 ,
,  ,
, 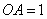 ,
, 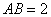 .
.
可得 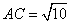 是等腰直角三角形.
是等腰直角三角形.
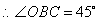 ,
, 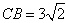 .
.
如图1,设抛物线对称轴与  轴交于点
轴交于点 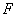 ,
,
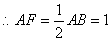 .
.
过点 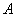 作
作 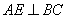 于点
于点  .
.
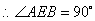 .
.
可得  ,
, 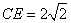 .
.
在 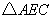 与
与 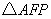 中,
中, 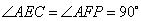 ,
,  ,
,
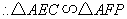 .
.
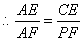 ,
, 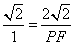 .
.
解得 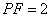 .
.
 点
点 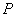 在抛物线的对称轴上,
在抛物线的对称轴上,
 点
点 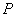 的坐标为
的坐标为 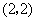 或
或 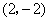 .······································································· 5分
.······································································· 5分
(3)解法一:如图2,作点 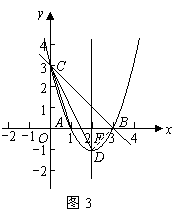 关于
关于 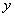 轴的对称点
轴的对称点  ,则
,则 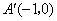 .
.
连结 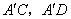 ,
,
 可得 可得 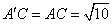 ,
, 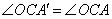 .
.
由勾股定理可得 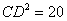 ,
,  .
.
又 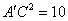 ,
,
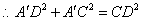 .
.
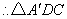 是等腰直角三角形,
是等腰直角三角形, 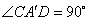 ,
,
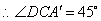 .
.
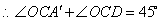 .
.
 .
.
 即 即 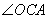 与
与 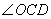 两角和的度数为
两角和的度数为 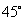 .·························································· 7分
.·························································· 7分
解法二:如图3,连结 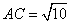 .
.
同解法一可得 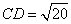 ,
, 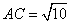 .
.
在 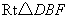 中,
中, 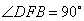 ,
, 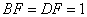 ,
,
 .
.
在 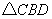 和
和 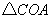 中,
中,
 ,
,  ,
, 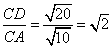 .
.
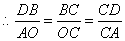 .
.
 .
.
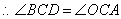 .
.
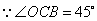 ,
,
 .
.
即 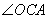 与
与 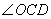 两角和的度数为
两角和的度数为 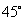 .·························································· 7分
.·························································· 7分
(08天津市卷)19.(本小题6分)
解二元一次方程组 
19.本小题满分6分.
解 ∵ 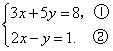
由②得  ,③ ······················································································ 2分 ,③ ······················································································ 2分
将③代入①,得 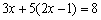 .解得 .解得 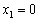 .代入③,得 .代入③,得  . .
∴原方程组的解为 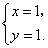 ·················································································· 6分 ·················································································· 6分
(08天津市卷)20.(本小题8分)
已知点P(2,2)在反比例函数 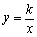 ( ( 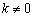 )的图象上, )的图象上,
(Ⅰ)当  时,求 时,求 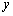 的值; 的值;
(Ⅱ)当  时,求 时,求 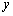 的取值范围. 的取值范围.
20.本小题满分8分.
解 (Ⅰ)∵点P(2,2)在反比例函数 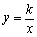 的图象上, 的图象上,
∴ 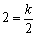 .即 .即 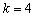 . ··························································································· 2分 . ··························································································· 2分
∴反比例函数的解析式为 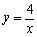 . .
∴当  时, 时, 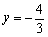 . ··················································································· 4分 . ··················································································· 4分
(Ⅱ)∵当 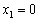 时, 时, 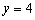 ;当 ;当 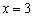 时, 时,  , ············································ 6分 , ············································ 6分
又反比例函数 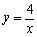 在 在  时 时 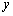 值随 值随 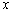 值的增大而减小, ···································· 7分 值的增大而减小, ···································· 7分
∴当  时, 时, 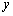 的取值范围为 的取值范围为 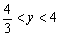 .······················································· 8分 .······················································· 8分
(08天津市卷)22.(本小题8分)
下图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时).
请分别计算这些车辆行驶速度的平均数、中位数和众数(结果精确到0.1).
22.本小题满分8分.
解 观察直方图,可得
车速为50千米/时的有2辆,车速为51千米/时的有5辆,
车速为52千米/时的有8辆,车速为53千米/时的有6辆,
车速为54千米/时的有4辆,车速为55千米/时的有2辆,
车辆总数为27, ······························································································· 2分
∴这些车辆行驶速度的平均数为
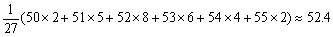 .····································· 4分 .····································· 4分
∵将这27个数据按从小到大的顺序排列,其中第14个数是52,
∴这些车辆行驶速度的中位数是52. ······························································ 6分
∵在这27个数据中,52出现了8次,出现的次数最多,
∴这些车辆行驶速度的众数是52.······································································· 8分
(08天津市卷)24.(本小题8分)注重:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路,填写表格,并完成本题解答的全过程.假如你选用其他的解题方案,此时,不必填写表格,只需按照解答题的一般要求,进行解答即可.
天津市奥林匹克中心体育场——“水滴”位于天津市西南部的奥林匹克中心内,某校九年级学生由距“水滴”10千米的学校出发前往参观,一部分同学骑自行车先走,过了20分钟后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度.
(Ⅰ)设骑车同学的速度为x千米/时,利用速度、时间、路程之间的关系填写下表.
(要求:填上适当的代数式,完成表格) |
|
速度(千米/时) |
所用时间(时) |
所走的路程(千米) | |
骑自行车 |
 
|
|
10 | |
乘汽车 |
|
|
10 | |
(Ⅱ)列出方程(组),并求出问题的解.
24.本小题满分8分.
解 (Ⅰ) |
|
速度(千米/时) |
所用时间(时) |
所走的路程(千米) | |
骑自行车 |
 
|
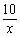
|
10 | |
乘汽车 |

|
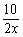
|
10 | |
·························································· 3分
(Ⅱ)根据题意,列方程得 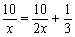 . ························································ 5分
. ························································ 5分
解这个方程,得 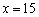 . ·············································································· 7分
. ·············································································· 7分
经检验, 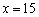 是原方程的根.
是原方程的根.
所以, 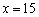 .
.
答:骑车同学的速度为每小时15千米. ····························································· 8分
(08天津市卷)26.(本小题10分)
已知抛物线  ,
,
(Ⅰ)若 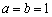 ,
, 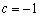 ,求该抛物线与
,求该抛物线与 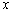 轴公共点的坐标;
轴公共点的坐标;
(Ⅱ)若 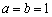 ,且当
,且当 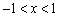 时,抛物线与
时,抛物线与 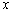 轴有且只有一个公共点,求
轴有且只有一个公共点,求  的取值范围;
的取值范围;
(Ⅲ)若  ,且
,且 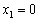 时,对应的
时,对应的 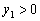 ;
; 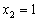 时,对应的
时,对应的 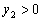 ,试判定当
,试判定当 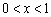 时,抛物线与
时,抛物线与 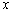 轴是否有公共点?若有,请证实你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证实你的结论;若没有,阐述理由.
26.本小题满分10分.
解(Ⅰ)当 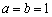 ,
, 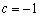 时,抛物线为
时,抛物线为 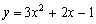 ,
,
方程  的两个根为
的两个根为  ,
, 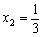 .
.
∴该抛物线与 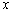 轴公共点的坐标是
轴公共点的坐标是 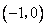 和
和 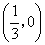 . ······································· 2分
. ······································· 2分
(Ⅱ)当 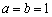 时,抛物线为
时,抛物线为 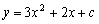 ,且与
,且与 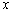 轴有公共点.
轴有公共点.
对于方程  ,判别式
,判别式 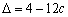 ≥0,有
≥0,有  ≤
≤ 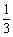 . ······························· 3分
. ······························· 3分
①当 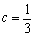 时,由方程
时,由方程 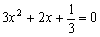 ,解得
,解得 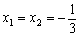 .
.
此时抛物线为 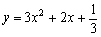 与
与 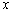 轴只有一个公共点
轴只有一个公共点 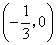 .························ 4分
.························ 4分
②当 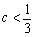 时,
时,
 时,
时,  ,
,
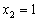 时,
时, 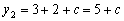 .
.
由已知 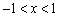 时,该抛物线与
时,该抛物线与 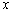 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为 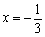 ,
,
应有  即
即 
解得 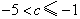 .
.
综上, 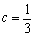 或
或 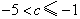 . ······································································· 6分
. ······································································· 6分
(Ⅲ)对于二次函数  ,
,
由已知 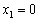 时,
时, 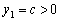 ;
; 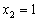 时,
时, 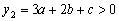 ,
,
又  ,∴
,∴ 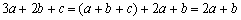 .
.
于是 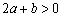 .而
.而 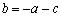 ,∴
,∴  ,即
,即 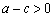 .
.
∴ 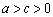 . ··································································································· 7分
. ··································································································· 7分
∵关于 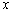 的一元二次方程
的一元二次方程 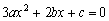 的判别式
的判别式
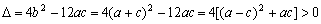 ,
,
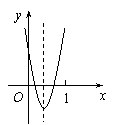 ∴抛物线
∴抛物线  与
与  轴有两个公共点,顶点在
轴有两个公共点,顶点在 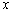 轴下方.···················· 8分
轴下方.···················· 8分
又该抛物线的对称轴 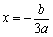 ,
,
由  ,
,  ,
, 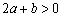 ,
,
得 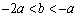 ,
,
∴ 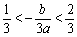 .
.
又由已知 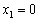 时,
时, 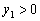 ;
; 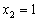 时,
时, 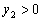 ,观察图象,
,观察图象,
可知在 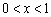 范围内,该抛物线与
范围内,该抛物线与 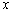 轴有两个公共点. ··································· 10分
轴有两个公共点. ··································· 10分
(08河北省卷)19.(本小题满分7分)
已知 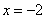 ,求
,求  的值.
的值.
19.解:原式 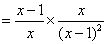
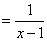 .
.
当 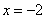 时,原式
时,原式 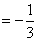 .
.
(08河北省卷)20.(本小题满分8分)
某种子培育基地用A,B,C,D四种型号的小麦种子共2 000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C型号种子的发芽率为 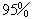 ,根据实验数据绘制了图10-1和图10-2两幅尚不完整的统计图.
,根据实验数据绘制了图10-1和图10-2两幅尚不完整的统计图.
(1)D型号种子的粒数是 ;
(2)请你将图10-2的统计图补充完整;
(3)通过计算说明,应选哪一个型号的种子进行推广;
(4)若将所有已发芽的种子放到一起,从中随机取出一粒,求取到B型号发芽种子的概率.
20.解:(1)500;
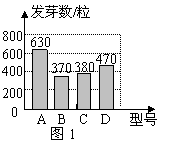 (2)如图1;
(2)如图1;
(3) 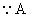 型号发芽率为
型号发芽率为  ,B型号发芽率为
,B型号发芽率为 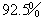 ,
,
D型号发芽率为  ,C型号发芽率为
,C型号发芽率为 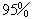 .
.
 应选C型号的种子进行推广.
应选C型号的种子进行推广.
(4) 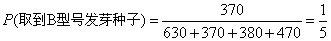 .
.
(08河北省卷)21.(本小题满分8分)
 如图11,直线
如图11,直线  的解析表达式为
的解析表达式为 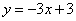 ,且
,且  与
与  轴交于点
轴交于点 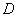 ,直线
,直线  经过点
经过点 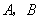 ,直线
,直线  ,
,  交于点
交于点  .
.
(1)求点 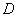 的坐标;
的坐标;
(2)求直线  的解析表达式;
的解析表达式;
(3)求 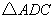 的面积;
的面积;
(4)在直线  上存在异于点
上存在异于点  的另一点
的另一点 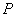 ,使得
,使得
 与
与 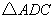 的面积相等,请直接写出点
的面积相等,请直接写出点 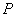 的坐标.
的坐标.
21.解:(1)由 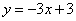 ,令
,令  ,得
,得 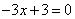 .
. 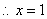 .
. 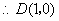 .
.
(2)设直线  的解析表达式为
的解析表达式为  ,由图象知:
,由图象知: 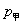 ,
,  ;
; 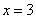 ,
,  .
.


 直线
直线  的解析表达式为
的解析表达式为 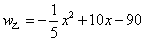 .
.
(3)由 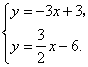 解得
解得 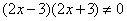
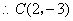 .
.
 ,
, 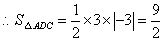 .
.
(4) 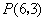 .
.
(08河北省卷)25.(本小题满分12分)
研究所对某种新型产品的产销情况进行了研究,为投资商在甲、乙两地生产并销售该产品提供了如下成果:第一年的年产量为  (吨)时,所需的全部费用
(吨)时,所需的全部费用 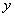 (万元)与
(万元)与  满足关系式
满足关系式  ,投入市场后当年能全部售出,且在甲、乙两地每吨的售价
,投入市场后当年能全部售出,且在甲、乙两地每吨的售价 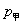 ,
, 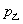 (万元)均与
(万元)均与  满足一次函数关系.(注:年利润=年销售额-全部费用)
满足一次函数关系.(注:年利润=年销售额-全部费用)
(1)成果表明,在甲地生产并销售  吨时,
吨时, 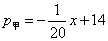 ,请你用含
,请你用含  的代数式表示甲地当年的年销售额,并求年利润
的代数式表示甲地当年的年销售额,并求年利润 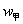 (万元)与
(万元)与  之间的函数关系式;
之间的函数关系式;
(2)成果表明,在乙地生产并销售  吨时,
吨时, 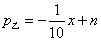 (
( 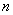 为常数),且在乙地当年的最大年利润为35万元.试确定
为常数),且在乙地当年的最大年利润为35万元.试确定 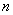 的值;
的值;
(3)受资金、生产能力等多种因素的影响,某投资商计划第一年生产并销售该产品18吨,根据(1),(2)中的结果,请你通过计算帮他决策,选择在甲地还是乙地产销才能获得较大的年利润?
参考公式:抛物线  的顶点坐标是
的顶点坐标是 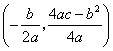 .
.
25.解:(1)甲地当年的年销售额为  万元;
万元;
 .
.
(2)在乙地区生产并销售时,
年利润 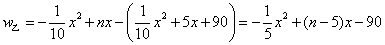 .
.
由  ,解得
,解得 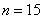 或
或 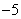 .
.
经检验,  不合题意,舍去,
不合题意,舍去, 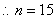 .
.
(3)在乙地区生产并销售时,年利润 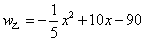 ,
,
将 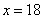 代入上式,得
代入上式,得 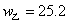 (万元);将
(万元);将 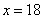 代入
代入  ,
,
得 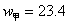 (万元).
(万元). 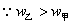 ,
,  应选乙地.
应选乙地.
(08内蒙古赤峰)19.(本题满分16分)
(1)解分式方程: 
19.(1)解:方程两边同乘 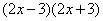 ,得
,得
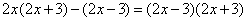 ······················································· (2分)
······················································· (2分)
化简,得 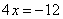 ······················································································· (5分)
······················································································· (5分)
解得 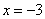 ··································································································· (7分)
··································································································· (7分)
检验: 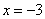 时
时 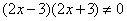 ,
, 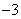 是原分式方程的解.···················· (8分)
是原分式方程的解.···················· (8分)
(2)假如 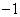 是一元二次方程
是一元二次方程 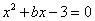 的一个根,求它的另一根.
的一个根,求它的另一根.
(2)解: 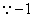 是
是 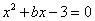 的一个根,
的一个根,
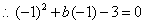 .
.
解方程得 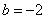 .························································································ (3分)
.························································································ (3分)
 原方程为
原方程为 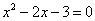
分解因式,得 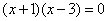
 ,
, 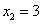 ························································································ (7分)
························································································ (7分)
 它的另一根是3.······················································································ (8分)
它的另一根是3.······················································································ (8分)
(08内蒙古赤峰)25.(本题满分14分)
在平面直角坐标系中给定以下五个点 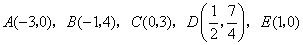 .
.
(1)请从五点中任选三点,求一条以平行于  轴的直线为对称轴的抛物线的解析式;
轴的直线为对称轴的抛物线的解析式;
(2)求该抛物线的顶点坐标和对称轴,并画出草图;
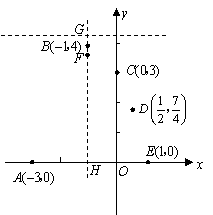 (3)已知点
(3)已知点  在抛物线的对称轴上,直线
在抛物线的对称轴上,直线  过点
过点 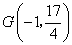 且垂直于对称轴.验证:以
且垂直于对称轴.验证:以  为圆心,
为圆心, 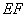 为半径的圆与直线
为半径的圆与直线  相切.请你进一步验证,以抛物线上的点
相切.请你进一步验证,以抛物线上的点 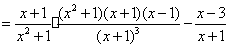 为圆心
为圆心 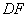 为半径的圆也与直线
为半径的圆也与直线  相切.由此你能猜想到怎样的结论.
相切.由此你能猜想到怎样的结论.
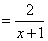 25.解:(1)设抛物线的解析式为
25.解:(1)设抛物线的解析式为 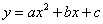 ,
,
且过点 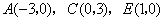 ,
,
由 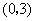 在
在 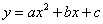 H .
H .
则 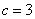 .……(2分)
.……(2分)
得方程组 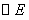 ,
,
解得 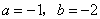 .
.
 抛物线的解析式为
抛物线的解析式为 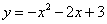 ············· (4分)
············· (4分)
(2)由  ·········· (6分)
·········· (6分)
得顶点坐标为  ,对称轴为
,对称轴为  .······· (8分)
.······· (8分)
(3)①连结 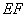 ,过点
,过点  作直线
作直线  的垂线,垂足为
的垂线,垂足为  ,
,
则 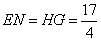 .
.
在 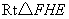 中,
中,  ,
, 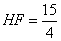 ,
,
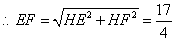 ,
,
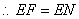 ,
,
 以
以  点为圆心,
点为圆心, 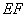 为半径的
为半径的 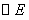 与直线
与直线  相切.·························· (10分)
相切.·························· (10分)
②连结 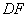 过点
过点  作直线
作直线  的垂线,垂足为
的垂线,垂足为 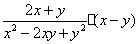 .过点
.过点 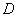 作
作  垂足为
垂足为 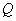 ,
,
则 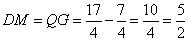 .
.
在  中,
中, 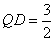 ,
,  .
.
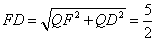 .
.
 以
以 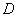 点为圆心
点为圆心 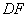 为半径的
为半径的 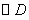 与直线
与直线  相切.····························· (12分)
相切.····························· (12分)
③以抛物线上任意一点 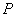 为圆心,以
为圆心,以 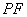 为半径的圆与直线
为半径的圆与直线  相切.·· (14分)
相切.·· (14分)
(08年内蒙古乌兰察布)19.(本小题8分)
先化简,再求值 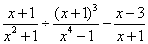 ,其中
,其中  .
.
19. 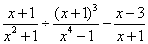
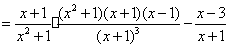
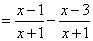
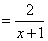 .
.
当  时,
时,

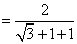
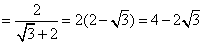 .
.
(08年内蒙古乌兰察布)20.(本小题6分)
在“不闯红灯,珍爱生命”活动中,文明中学的关欣和李好两位同学某天来到城区中心的十字路口,观察,统计上午7:00—12:00中闯红灯的人次,制作了如下的两个数据统计图.
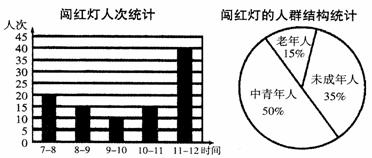
(1)通过计算,估计一个月(30天)上午7:00—12:00在该十字路口闯红灯的老年人约有多少次;
(2)请你根据统计图提供的信息向交通治理部门提出一条合理化建议.
20.(1) 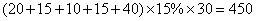 (人).
(人).
(2)加强对11:00—12:00这一时段的交通治理,或加强对中青年人(或未成年人)交通安全教育.
注:建议要合理,思想要积极向上.
(08年内蒙古乌兰察布)22.(本小题10分)
在一次春游中,小明、小亮等同学随家人一同到江郎山旅游,下面是购买门票时,小明与他爸爸的对话(如图所示).

(1)小明他们一共去了几个成人?几个学生?
(2)请你帮助小明算一算,用哪种方式买票更省钱?并说明理由.
22.解:(1)设小明他们一共了  个成人,
个成人, 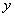 个学生,
个学生,
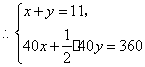

答:小明他们一共去了7个成人,4个学生.
(2)若按14人购买团体票,则共需  (元)
(元)
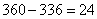 (元).
(元).
 购买团体票可省24元.
购买团体票可省24元.
(08年内蒙古乌兰察布)23.(本小题11分)
声音在空气中传播的速度 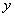 (m/s)是气温
(m/s)是气温  (℃)的一次函数,下表列出了一组不同气温的音速:
(℃)的一次函数,下表列出了一组不同气温的音速:
|
气温  (℃) (℃) |
0 |
5 |
10 |
15 |
20 |
|
音速 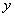 (m/s) (m/s) |
331 |
334 |
337 |
340 |
343 |
(1)求 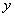 与
与  之间的函数关系式;
之间的函数关系式;
(2)气温 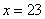 ℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
23.解:(1)设  ,
,
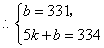
 ,
, 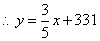
(2)当 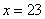 时,
时, 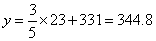 .
.
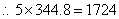 .
.
 此人与烟花燃放地相距约1724m.
此人与烟花燃放地相距约1724m.
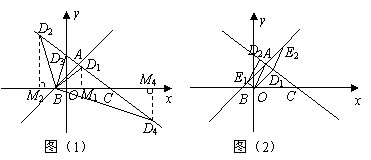
(08年内蒙古乌兰察布)24.(本小题14分)
两个直角边为6的全等的等腰直角三角形 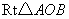 和
和 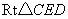 ,按如图一所示的位置放置,点
,按如图一所示的位置放置,点  与
与  重合.
重合.
(1)  固定不动,
固定不动,  沿
沿  轴以每秒2个单位长度的速度向右运动,当点
轴以每秒2个单位长度的速度向右运动,当点  运动到与点
运动到与点 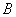 重合时停止,设运动
重合时停止,设运动  秒后,
秒后, 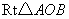 和
和 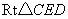 的重叠部分面积为
的重叠部分面积为 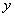 ,求
,求 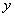 与
与  之间的函数关系式;
之间的函数关系式;
(2)当 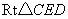 以(1)中的速度和方向运动,运动时间
以(1)中的速度和方向运动,运动时间 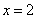 秒时,
秒时, 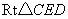 运动到如图二所示的位置,若抛物线
运动到如图二所示的位置,若抛物线 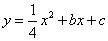 过点
过点 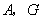 ,求抛物线的解析式;
,求抛物线的解析式;
(3)现有一动点 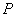 在(2)中的抛物线上运动,试问点
在(2)中的抛物线上运动,试问点 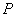 在运动过程中是否存在点
在运动过程中是否存在点 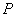 到
到  轴或
轴或 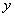 轴的距离为2的情况,若存在,请求出点
轴的距离为2的情况,若存在,请求出点 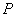 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
24.解:(1)由题意知重叠部分是等腰直角三角形,作  .
.
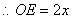 ,
, 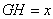 ,
,
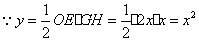 (
( 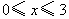 )
)
(2) 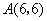 )
)
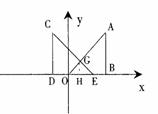 当
当 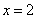 时,
时,  .
.
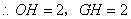 ,
,  .
.
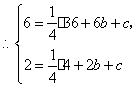

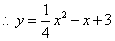 .
.
(3)设 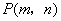 .
.
当点 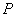 到
到 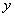 轴的距离为
轴的距离为 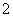 时,有
时,有  ,
, 
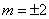 .
.
当  时,得
时,得  ,
,
当 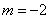 时,得
时,得 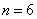 .
.
当点 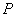 到
到  轴的距离为2时,有
轴的距离为2时,有 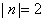 .
.
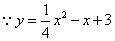

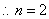 .
.
当 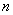
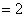 时,得
时,得  .
.
综上所述,符合条件的点 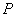 有两个,分别是
有两个,分别是  .
.
(08山西省卷)19.(本题8分)求代数式的值:  ,其中
,其中 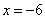 。
。
(08山西省卷)21.(本题10分)“安全教育,警钟长鸣”,为此某校从14000名学生中随机抽取了200名学生就安全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图)。
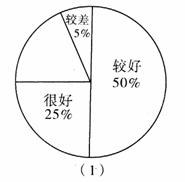
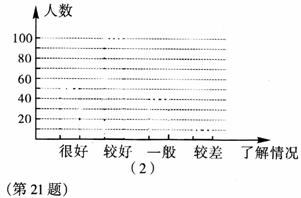
(1)补全扇形统计图,并计算这200名学生中对安全知识了解“较好”、“很好”的总人数。(2)在图(2)中,绘制样本频数的条形统计图。
(3)根据以上信息,请提出一条合理化建议。
(08山西省卷)22.(本题10分)甲、乙两人在玩转盘游戏时,把转盘A、B分成3等份、4等份,并在每一份内标有数字(如图)。
游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲胜;指针所在区域的数字之积为偶数时,乙胜。假如指针恰好在分割线上,则需重新转动转盘。
(1)用树状图或列表的方法,求甲获胜的概率。
(2)这个游戏规则对甲、乙双方公平吗?请判定并说明理由。
(08山西省卷)24.(本题8分)某文化用品商店用200元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元。
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
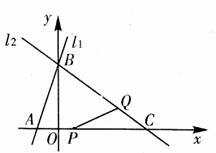 (08山西省卷)26.(本题14分)如图,已知直线
(08山西省卷)26.(本题14分)如图,已知直线  的解析式为
的解析式为 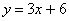 ,直线
,直线 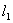 与x轴、y轴分别相交于A、B两点,直线
与x轴、y轴分别相交于A、B两点,直线 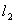 经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线
经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线 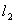 从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(
从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒( 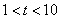 )。
)。
(1)求直线 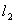 的解析式。
的解析式。
(2)设△PCQ的面积为S,请求出S关于t的函数关系式。
(3)试探究:当t为何值时,△PCQ为等腰三角形?
(08山西太原)21.(本小题满分5分)
解不等式组: 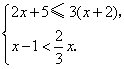
21.解:解不等式  ,得
,得 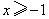 .············································· 2分
.············································· 2分
解不等式 
 ,得
,得 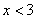 .········································································· 4分
.········································································· 4分
所以,原不等式组的解集是 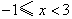 .····························································· 5分
.····························································· 5分
(08山西太原)22.(本小题满分5分)
解方程: 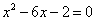 .
.
22.解法一:这里 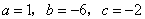 .························································ 1分
.························································ 1分
 ,························································· 2分
,························································· 2分
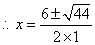 .································································································· 3分
.································································································· 3分
即 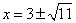 .·································································································· 4分
.·································································································· 4分
所以,方程的解为 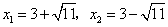 .··················································· 5分
.··················································· 5分
解法二:配方,得 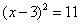 .········································································ 3分
.········································································ 3分
即 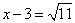 或
或 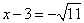 .·········································································· 4分
.·········································································· 4分
所以,方程的解为 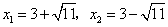 .··················································· 5分
.··················································· 5分
(08山西太原)23.(本小题满分6分)
为帮助灾区人民重建家园,某校学生积极捐款.已知第一次捐款总额为9000元,第二次捐款总额为12000元,两次人均捐款额相等,但第二次捐款人数比第一次多50人.求该校第二次捐款的人数.
23.解法一:设第二次捐款人数为  人,则第一次捐款人数为
人,则第一次捐款人数为 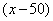 人.·········· 1分
人.·········· 1分
根据题意,得 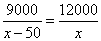 .·········································································· 3分
.·········································································· 3分
解这个方程,得  .··················································································· 4分
.··················································································· 4分
经检验,  是所列方程的根.····································································· 5分
是所列方程的根.····································································· 5分
答:该校第二次捐款人数为200人.···································································· 6分
解法二:人均捐款额为 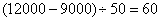 (元).····································· 3分
(元).····································· 3分
第二次捐款人数为  (人).························································ 5分
(人).························································ 5分
答:该校第二次捐款人数为200人.···································································· 6分
(08山西太原)25.(本小题满分10分)
甲乙两名同学做摸牌游戏.他们在桌上放了一副扑克牌中的4张牌,牌面分别是J,Q,K,K.游戏规则是:将牌面全部朝下,从这4张牌中随机取1张牌记下结果放回,洗匀后再随机取1张牌,若两次取出的牌中都没有K,则甲获胜,否则乙获胜.你认为甲乙两人谁获胜的可能性大?用列表或画树状图的方法说明理由.
25.解:乙获胜的可能性大.·············································································· 2分
进行一次游戏所有可能出现的结果如下表:·························································· 6分
|
 第二次 第二次
第一次 |
J |
Q |
K1 |
K2 |
|
J |
(J,J) |
(J,Q) |
(J,K1) |
(J,K2) |
|
Q |
(Q,J) |
(Q,Q) |
(Q,K1) |
(Q,K2) |
|
K1 |
(K1,J) |
(K1,Q) |
(K1,K1) |
(K1,K2) |
|
K2 |
(K2,J) |
(K2,Q) |
(K2,K1) |
(K2,K2) |
从上表可以看出,一次游戏可能出现的结果共有16种,而且每种结果出现的可能性相等,其中两次取出的牌中都没有K的有(J,J),(J,Q),(Q,J),(Q,Q)等4种结果.
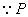 (两次取出的牌中都没有K)
(两次取出的牌中都没有K) 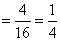 .
.
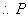 (甲获胜)
(甲获胜) 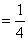 ,
, 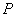 (乙获胜)
(乙获胜) 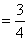 .························································· 9分
.························································· 9分

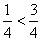 ,
,  乙获胜的可能性大.······································································ 10分
乙获胜的可能性大.······································································ 10分
(08山西太原)26.(本小题满分6分)
人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄.当车速为50km/h时,视野为80度.假如视野  (度)是车速
(度)是车速 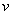 (km/h)的反比例函数,求
(km/h)的反比例函数,求 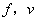 之间的关系式,并计算当车速为100km/h时视野的度数.
之间的关系式,并计算当车速为100km/h时视野的度数.
26.解:设 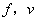 之间的关系式为
之间的关系式为  .··············································· 1分
.··············································· 1分
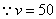 时,
时, 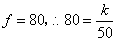 .······································································ 2分
.······································································ 2分
解,得 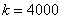 .······························································································· 3分
.······························································································· 3分
所以, 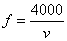 .····························································································· 4分
.····························································································· 4分
当 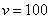 时,
时, 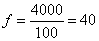 (度).································································ 5分
(度).································································ 5分
答:当车速为100km/h时视野为40度.······························································· 6分
(08山西太原)27.(本小题满分10分)
用商家免费提供的塑料袋购物,我们享受着方便和快捷,但同时要关注它对环境的潜在危害.为了解太原市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:
|
每户丢弃塑料袋数(单位:个) |
1 |
2 |
3 |
4 |
5 |
6 |
|
家庭数(单位:户) |
15 |
60 |
65 |
35 |
20 |
5 |
(1)求这天这200户家庭平均每户丢弃塑料袋的个数.
(2)假设我市现有家庭100万户,据此估计全市所有家庭每年(以365天计算)丢弃塑料袋的总数.
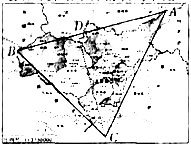
(3)下图是我市行政区划图,它的面积相当于图中  的面积.已知
的面积.已知  间的实际距离为150km,
间的实际距离为150km,  间的实际距离为110km,
间的实际距离为110km, 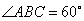 .根据(2)中的估算结果,求我市每年每平方公里的土地上会增加多少个塑料袋?(取
.根据(2)中的估算结果,求我市每年每平方公里的土地上会增加多少个塑料袋?(取 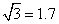 ,
, 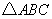 的面积和最后计算结果都精确到千位)
的面积和最后计算结果都精确到千位)
27.解:(1) 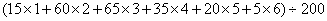
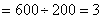 (个/户).··························································· 2分
(个/户).··························································· 2分
所以,这天这200户家庭平均每户丢弃3个塑料袋.············································ 3分
(2) 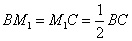 (万个).······························································· 5分
(万个).······························································· 5分
所以,我市所有家庭每年丢弃109500万个塑料袋.·············································· 6分
(3)如图,过点  作
作 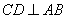 ,垂足为点
,垂足为点 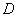 .················································ 7分
.················································ 7分
在 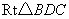 中,
中,  ,
,
由 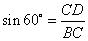 ,得
,得  .················································ 8分
.················································ 8分
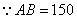 ,
,
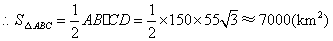 .····································· 9分
.····································· 9分
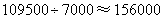 (个/km2).
(个/km2).
答:我市每年平均每平方公里的土地上会增加156000个塑料袋.······················· 10分
(08山西太原)29.(本小题满分12分)
 如图,在平面直角坐标系
如图,在平面直角坐标系 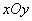 中,直线
中,直线  与
与 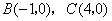 交于点
交于点 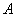 ,分别交
,分别交  轴于点
轴于点 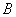 和点
和点  ,点
,点 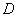 是直线
是直线 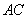 上的一个动点.
上的一个动点.
(1)求点 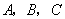 的坐标.
的坐标.
(2)当 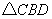 为等腰三角形时,求点
为等腰三角形时,求点 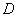 的坐标.
的坐标.
(3)在直线 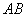 上是否存在点
上是否存在点  ,使得以点
,使得以点 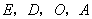 为顶点的四边形是平行四边形?假如存在,直线写出
为顶点的四边形是平行四边形?假如存在,直线写出 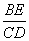 的值;假如不存在,请说明理由.
的值;假如不存在,请说明理由.
29.解:(1)在  中,当
中,当  时,
时, 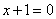 ,
,
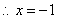 ,点
,点 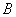 的坐标为
的坐标为  .······································································· 1分
.······································································· 1分
在 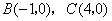 中,当
中,当  时,
时, 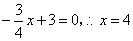 ,点
,点  的坐标为(4,0). 2分
的坐标为(4,0). 2分
由题意,得  解得
解得 
 点
点 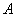 的坐标为
的坐标为  .·················································································· 3分
.·················································································· 3分
(2)当 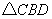 为等腰三角形时,有以下三种情况,如图(1).设动点
为等腰三角形时,有以下三种情况,如图(1).设动点 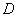 的坐标为
的坐标为 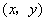 .
.
由(1),得 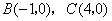 ,
, 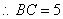 .
.
①当  时,过点
时,过点  作
作  轴,垂足为点
轴,垂足为点  ,则
,则 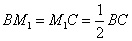 .
.
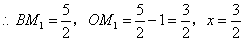 .
.
 ,点
,点 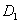 的坐标为
的坐标为 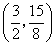 .·············································· 4分
.·············································· 4分
②当 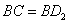 时,过点
时,过点 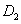 作
作  轴,垂足为点
轴,垂足为点 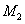 ,则
,则 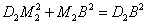 .
.
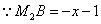 ,
,  ,
,
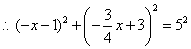 .
.
解,得  (舍去).此时,
(舍去).此时, 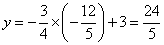 .
.
 点
点 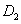 的坐标为
的坐标为  .··········································································· 6分
.··········································································· 6分
③当 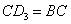 ,或
,或 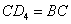 时,同理可得
时,同理可得 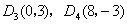 .·················· 9分
.·················· 9分
由此可得点 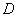 的坐标分别为
的坐标分别为  .
.
评分说明:符合条件的点有4个,正确求出1个点的坐标得1分,2个点的坐标得3分,3个点的坐标得5分,4个点的坐标得满分;与所求点的顺序无关.
(3)存在.以点 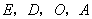 为顶点的四边形是平行四边形有以下三种情形,如图(2).
为顶点的四边形是平行四边形有以下三种情形,如图(2).
①当四边形 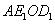 为平行四边形时,
为平行四边形时, 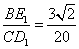 .········································ 10分
.········································ 10分
②当四边形 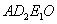 为平行四边形时,
为平行四边形时, 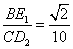 .········································· 11分
.········································· 11分
③当四边形 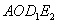 为平行四边形时,
为平行四边形时,  .····································· 12分
.····································· 12分
评分说明:1.如你的正确解法与上述提供的参考答案不同时,可参照评分说明进行估分.
2.如解答题由多个问题组成,前一问解答有误或未答,对后面问题的解答没有影响.可依据参考答案及评分说明进行估分.
来源:中国哲士网
教师学生家长 数中考复习资料 备课考试教学
教育资料 [组图]中考数学代数解答题 文章
|
| 上一篇文章: 与圆有关的基本概念 |
| 下一篇文章: 中考数学代数选择题 |
| |
|
![]() . ························································ 5分
. ························································ 5分![]() . ·············································································· 7分
. ·············································································· 7分![]() 是原方程的根.
是原方程的根. ![]() .
. ![]() ,
,![]() ,
, ![]() ,求该抛物线与
,求该抛物线与 ![]() 轴公共点的坐标;
轴公共点的坐标;![]() ,且当
,且当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴有且只有一个公共点,求
轴有且只有一个公共点,求 ![]() 的取值范围;
的取值范围;![]() ,且
,且 ![]() 时,对应的
时,对应的 ![]() ;
; ![]() 时,对应的
时,对应的 ![]() ,试判定当
,试判定当 ![]() 时,抛物线与
时,抛物线与 ![]() 轴是否有公共点?若有,请证实你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证实你的结论;若没有,阐述理由.![]() ,
, ![]() 时,抛物线为
时,抛物线为 ![]() ,
,![]() 的两个根为
的两个根为 ![]() ,
, ![]() .
. ![]() 轴公共点的坐标是
轴公共点的坐标是 ![]() 和
和 ![]() . ······································· 2分
. ······································· 2分![]() 时,抛物线为
时,抛物线为 ![]() ,且与
,且与 ![]() 轴有公共点.
轴有公共点.![]() ,判别式
,判别式 ![]() ≥0,有
≥0,有 ![]() ≤
≤ ![]() . ······························· 3分
. ······························· 3分![]() 时,由方程
时,由方程 ![]() ,解得
,解得 ![]() .
.![]() 与
与 ![]() 轴只有一个公共点
轴只有一个公共点 ![]() .························ 4分
.························ 4分![]() 时,
时, ![]() 时,
时, ![]() ,
,![]() 时,
时, ![]() .
.![]() 时,该抛物线与
时,该抛物线与 ![]() 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为 ![]() ,
, 即
即 ![]()
![]() .
.![]() 或
或 ![]() . ······································································· 6分
. ······································································· 6分![]() ,
,![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,
,![]() ,∴
,∴ ![]() .
.![]() .而
.而 ![]() ,∴
,∴ ![]() ,即
,即 ![]() .
.![]() . ··································································································· 7分
. ··································································································· 7分![]() 的一元二次方程
的一元二次方程 ![]() 的判别式
的判别式![]() ,
,  ∴抛物线
∴抛物线 ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() .
.![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,观察图象,
,观察图象,![]() 范围内,该抛物线与
范围内,该抛物线与 ![]() 轴有两个公共点. ··································· 10分
轴有两个公共点. ··································· 10分![]() ,求
,求 ![]() 的值.
的值.![]()
![]() .
.![]() 时,原式
时,原式 ![]() .
.![]() ,根据实验数据绘制了图10-1和图10-2两幅尚不完整的统计图.
,根据实验数据绘制了图10-1和图10-2两幅尚不完整的统计图.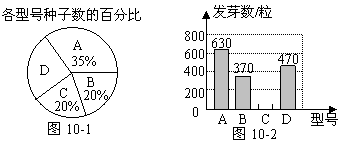
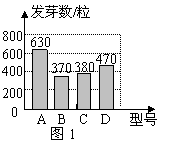 (2)如图1;
(2)如图1;
![]() 型号发芽率为
型号发芽率为 ![]() ,B型号发芽率为
,B型号发芽率为 ![]() ,
,![]() ,C型号发芽率为
,C型号发芽率为 ![]() .
.![]() 应选C型号的种子进行推广.
应选C型号的种子进行推广.![]() .
. 如图11,直线
如图11,直线 ![]() 的坐标;
的坐标;![]() 的解析表达式;
的解析表达式;![]() 的面积;
的面积;![]() 上存在异于点
上存在异于点 ![]() 的另一点
的另一点 ![]() ,使得
,使得![]() 与
与 ![]() 的面积相等,请直接写出点
的面积相等,请直接写出点 ![]() 的坐标.
的坐标.![]() ,令
,令 ![]() ,得
,得 ![]() .
. ![]() .
. ![]() .
.![]() 的解析表达式为
的解析表达式为 ![]() ,由图象知:
,由图象知: ![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.

![]() 直线
直线 ![]() 的解析表达式为
的解析表达式为 ![]() .
.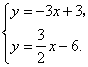 解得
解得 ![]()
![]() .
.![]() ,
, ![]() .
.![]() .
.![]() (吨)时,所需的全部费用
(吨)时,所需的全部费用 ![]() (万元)与
(万元)与 ![]() 满足关系式
满足关系式 ![]() ,投入市场后当年能全部售出,且在甲、乙两地每吨的售价
,投入市场后当年能全部售出,且在甲、乙两地每吨的售价 ![]() ,
, ![]() (万元)均与
(万元)均与 ![]() 满足一次函数关系.(注:年利润=年销售额-全部费用)
满足一次函数关系.(注:年利润=年销售额-全部费用)![]() 吨时,
吨时, ![]() ,请你用含
,请你用含 ![]() 的代数式表示甲地当年的年销售额,并求年利润
的代数式表示甲地当年的年销售额,并求年利润 ![]() (万元)与
(万元)与 ![]() 之间的函数关系式;
之间的函数关系式;![]() 吨时,
吨时, ![]() (
( ![]() 为常数),且在乙地当年的最大年利润为35万元.试确定
为常数),且在乙地当年的最大年利润为35万元.试确定 ![]() 的值;
的值;![]() 的顶点坐标是
的顶点坐标是 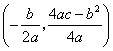 .
.![]() 万元;
万元;![]() .
.![]() .
. ,解得
,解得 ![]() 或
或 ![]() .
.![]() 不合题意,舍去,
不合题意,舍去, ![]() .
.![]() ,
,![]() 代入上式,得
代入上式,得 ![]() (万元);将
(万元);将 ![]() 代入
代入 ![]() ,
,![]() (万元).
(万元). ![]() ,
, ![]() 应选乙地.
应选乙地.![]()
![]() ,得
,得![]() ······················································· (2分)
······················································· (2分)![]() ······················································································· (5分)
······················································································· (5分)![]() ··································································································· (7分)
··································································································· (7分)![]() 时
时 ![]() ,
, ![]() 是原分式方程的解.···················· (8分)
是原分式方程的解.···················· (8分)![]() 是一元二次方程
是一元二次方程 ![]() 的一个根,求它的另一根.
的一个根,求它的另一根.![]() 是
是 ![]() 的一个根,
的一个根,![]() .
.![]() .························································································ (3分)
.························································································ (3分)![]() 原方程为
原方程为 ![]()
![]()
![]() ,
, ![]() ························································································ (7分)
························································································ (7分)![]() 它的另一根是3.······················································································ (8分)
它的另一根是3.······················································································ (8分)![]() .
.![]() 轴的直线为对称轴的抛物线的解析式;
轴的直线为对称轴的抛物线的解析式; (3)已知点
(3)已知点 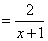 25.解:(1)设抛物线的解析式为
25.解:(1)设抛物线的解析式为 ![]() ,
,![]() 在
在 ![]() H .
H .![]() .……(2分)
.……(2分)![]() ,
,![]() .
.![]() 抛物线的解析式为
抛物线的解析式为 ![]() ············· (4分)
············· (4分)![]() ·········· (6分)
·········· (6分)![]() ,对称轴为
,对称轴为 ![]() .······· (8分)
.······· (8分)![]() ,过点
,过点 ![]() 作直线
作直线 ![]() 的垂线,垂足为
的垂线,垂足为 ![]() ,
,![]() .
.![]() 中,
中, ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() 以
以 ![]() 点为圆心,
点为圆心, ![]() 为半径的
为半径的 ![]() 与直线
与直线 ![]() 相切.·························· (10分)
相切.·························· (10分)![]() 过点
过点 ![]() 作直线
作直线 ![]() 的垂线,垂足为
的垂线,垂足为 ![]() .过点
.过点 ![]() 作
作 ![]() 垂足为
垂足为 ![]() ,
,![]() .
.![]() 中,
中, ![]() ,
, ![]() .
.![]() .
.![]() 以
以 ![]() 点为圆心
点为圆心 ![]() 为半径的
为半径的 ![]() 与直线
与直线 ![]() 相切.····························· (12分)
相切.····························· (12分)![]() 为圆心,以
为圆心,以 ![]() 为半径的圆与直线
为半径的圆与直线 ![]() 相切.·· (14分)
相切.·· (14分)![]() ,其中
,其中 ![]() .
.![]()
![]()
![]()
![]() .
.![]() 时,
时,![]()
![]()
![]() .
.
![]() (人).
(人).
![]() 个成人,
个成人, ![]() 个学生,
个学生,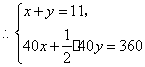
![]()
![]() (元)
(元)![]() (元).
(元).![]() 购买团体票可省24元.
购买团体票可省24元.![]() (m/s)是气温
(m/s)是气温 ![]() (℃)的一次函数,下表列出了一组不同气温的音速:
(℃)的一次函数,下表列出了一组不同气温的音速:![]() 与
与 ![]() 之间的函数关系式;
之间的函数关系式;![]() ℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?![]() ,
,![]()
![]() ,
, ![]()
![]() 时,
时, ![]() .
.![]() .
.![]() 此人与烟花燃放地相距约
此人与烟花燃放地相距约![]() 和
和 ![]() ,按如图一所示的位置放置,点
,按如图一所示的位置放置,点 ![]() 与
与 ![]() 重合.
重合.
![]() 固定不动,
固定不动, ![]() 沿
沿 ![]() 轴以每秒2个单位长度的速度向右运动,当点
轴以每秒2个单位长度的速度向右运动,当点 ![]() 运动到与点
运动到与点 ![]() 重合时停止,设运动
重合时停止,设运动 ![]() 秒后,
秒后, ![]() 和
和 ![]() 的重叠部分面积为
的重叠部分面积为 ![]() ,求
,求 ![]() 与
与 ![]() 之间的函数关系式;
之间的函数关系式;![]() 以(1)中的速度和方向运动,运动时间
以(1)中的速度和方向运动,运动时间 ![]() 秒时,
秒时, ![]() 运动到如图二所示的位置,若抛物线
运动到如图二所示的位置,若抛物线 ![]() 过点
过点 ![]() ,求抛物线的解析式;
,求抛物线的解析式;![]() 在(2)中的抛物线上运动,试问点
在(2)中的抛物线上运动,试问点 ![]() 在运动过程中是否存在点
在运动过程中是否存在点 ![]() 到
到 ![]() 轴或
轴或 ![]() 轴的距离为2的情况,若存在,请求出点
轴的距离为2的情况,若存在,请求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.![]() .
.![]() ,
, ![]() ,
,![]() (
( ![]() )
)![]() )
) 当
当 ![]() 时,
时, ![]() .
.![]() ,
, ![]() .
.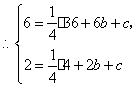
![]()
![]() .
.![]() .
.![]() 到
到 ![]() 轴的距离为
轴的距离为 ![]() 时,有
时,有 ![]() ,
, ![]()
![]() .
.![]() 时,得
时,得 ![]() ,
,![]() 时,得
时,得 ![]() .
.![]() 到
到 ![]() 轴的距离为2时,有
轴的距离为2时,有 ![]() .
.![]()
![]()
![]() .
.![]()
![]() 时,得
时,得 ![]() .
.![]() 有两个,分别是
有两个,分别是 ![]() .
.![]()
![]()


 (08山西省卷)26.(本题14分)如图,已知直线
(08山西省卷)26.(本题14分)如图,已知直线 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
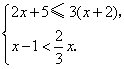
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 如图,在平面直角坐标系
如图,在平面直角坐标系 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()