一、选择题: 本大题共12小题；每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1． 
A． 
２．下列运算中，正确的是 （ ）
A． 
3．点P(1，―2)关于y轴对称的点的坐标是 （ ）
A．(―1，―2) B．(1， 2) C． (―1，2) D． (―2，1)
4．据统计，2005“超级女声”短信投票的总票数约327 000 000张，将这个数写成科学计数法是 （ ）
A． 
5．不等式组 
A．－1 B．0 C．1 D．4
6．如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的一个动点，则线段OM长的最小值为 （ ）
A．2 B．3 C．4 D．5
|
A |
|
O |
|
B |
|
M |
第6题图
7．如图，是象棋盘的一部分，若帅位于点（1，－2）上，相位于点（3，－2）上，则炮位于点 （ ）
A．（－1，1） B．（－1，2） C．（－2，2） D．（－2，1）
8．如图，把一个正方形三次对折后沿虚线剪下则得到的图形是 ( )
A B C D
9．我们知道，溶液的酸碱度由pH确定．当pH＞7时，溶液呈碱性；当pH＜7时，溶液呈酸性．若将给定的HCI溶液加水稀释，那么在下列图象中，能反映HCI溶液的pH与所加水的体积（v）的变化关系的是 （ ）
A B C D
|
80cm |
|
x |
|
x |
|
x |
|
x |
|
50cm |
10． 在一幅长80cm，宽50cm的矩形风景画的四面镶一 条金色纸边，制成一幅矩形挂图，如图所示，假如要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的方程是 （ ）
A．x2 130x-1400=0 B．x2-65x-350=0
C．x2-130x-1400=0 D．x2 65x-350=0
11．甲、乙、丙三位同学进行立定跳远比赛，每人轮流跳一次称为一轮，每轮按名次从高到低分别得3分、2分、1分（没有并列名次）．他们一共进行了五轮比赛，结果甲共得14分；乙第一轮得3分，第二轮得1分，且总分最低.那么丙得到的分数是 （ ）
A．8分 B．9分 C．10分 D．11分
12．如图：这是圆桌正上方的灯泡（看作一个点）发出的光线照射桌面后，在地面上形成阴影（圆形）的示意图，已知桌面的直径为1.2米，桌面距离地面1米，若灯泡距离地面3米，则地面上阴影部分的面积为 （ ）
A． 
平方米 B． 
平方米
C． 
平方米 D． 
平方米
二、填空题:本大题共10小题；每小题3分，共30分．把答案填写在题中横线上．
13．分解因式： 
14．已知函数：（1）图象经过（－2，１），（2）函数值y随x值的增大而增大．请你写出一个同时满足（1）和（2）的函数表达式 .
15．某班有49位学生，其中有21位女生. 在一次活动中，班上每一位学生的名字都各自写在一张小纸条上，放入一盒中搅匀. 假如老师闭上眼睛从盒中随机抽出一张纸条，那么抽到写有女生名字纸条的概率是 .
16． 棱长是1cm的小立方体组成如图所示的几何体，那么这个几何体的表面积是 ．
 |
第16题图 第17题图
17．在右边的日历中， 任意圈出一竖列上相邻的三个数，设中间的一个数n， 则这三个数之和为________（用含n的代数式表示）．
18． 一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分（如图4），则这串珠子被盒子遮住的部分有____ 颗.
19．如图：用8块相同的长方形地砖拼成一个矩形，则每个长方形地砖的面积是 ．
第18题图
20．一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是 个单位.
21．如图，平行四边形ABCD的周长为16cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为__________㎝
22． 如图，在边长为２的正方形内部，以各边为直径画四个半 圆，则图中阴影部分的面积是 ．
|
密 |
|
封 |
|
线 |
三、解答题：（本题共8个小题，共54分）
23．（本小题5分）计算： 
24．（本小题5分）
先化简代数式 
25．(本小题5分) 解方程： 
26.(本题7分) 如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG.
(1) 观察猜想BE与DG之间的大小关系，并证实你的结论;
|
A |
|
B |
|
C |
|
D |
|
E |
|
F |
|
G |
(2) 图中是否存在通过旋转能够互相重合的两个三角形? 若存在，请说出旋转过程; 若不存在，请说明理由.
27．（本题７分）城市规划期间，欲拆除一电线杆ＡＢ（如图），已知与电线杆ＡＢ水平距离14米的D处有一等腰梯形大坝CDEF，该梯形的上底CF长为3米，下底DE长为5米，
∠CDE=60°，在坝顶C处测得杆顶A的仰角为30°,D、G之间是宽3米的人行道．试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封闭?请说明理由．（在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域）
|
D |
|
A |
|
B |
|
C |
|
F |
|
E |
|
人行道 |
|
G |
|
30° |
  |
28．(本题9分) 某地区为了改善生态环境，防止水土流失，决定从2003年起开始“退耕还林”，在山坡上推广种植某种果树，并且出台了一项激励措施：在“退耕还林”的过程中，每一年新增果树达到100棵的农户，当年都可得到生活补贴1200元，且每超出一棵，政府还给予每棵 
下表是某农户在头两年通过“退耕还林”每年获得的总收入情况：
年 份
新增果树的棵数
年总收入
2003年
130棵
1500元
2004年
150棵
4300元
(注：年总收入＝生活补贴费＋政府奖励费＋果实收入)
（１）试根据以上提供的资料确定
（２）从2005年起，该农户每年新增果树的棵数将以某一百分率增长，预计2006年新增果树216棵，那么2006年该农户通过“退耕还林”获得的年总收入将达到多少元？
29．（本题7分） 如图，在矩形ABCD中，AB=3，AD=2，点E、F分别在AB、DC上，AE=DF=2.再把一块直径为2的量角器（圆心为O）放置在图形上，使其0°线MN与EF重合；若将量角器0°线上的端点N固定在点F上，再把量角器绕点F顺时针方向旋转∠α（0°<α<90°）,此时量角器的半圆弧与EF相交于点P，设点P处量角器的读数为 
（1）用含
（2）当 
 |
30．（本题9分） 如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0），（3，4）.动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于P，连结MP. 已知动点运动了 
（1）P点的坐标为（ ， ）；（用含x的代数式表示）
（2）试求 △MPA面积的最大值，并求此时x的值。
（3）请你探索：当x为何值时，△MPA是一个等腰三角形？
你发现了几种情况？写出你的研究成果。
答 案
一、选择题：
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
A
C
B
B
D
C
C
D
B
B
二、填空题：
13、3x(x 3)(x-3)； 14、答案不惟一，如y=2x 5等； 15、 
18、27； 19、300 
三、解答题：
23、原式= 
24、原式= 
25、解：去分母，得 2x(1 x)=2(x-1)(x 1) x-1
解这个方程，得 x=-3
经检验 x=-3是原方程的根，所以原方程的根是x=-3
26、(1)、猜想：BE=DG
证实：∵ 四边形ABCD、ECGF都是正方形
∴ BC=DC ∠BCE=∠DCG=90° EC=DG
∴ △BCE≌DCG
∴ BE=DG
（2）、这样的两个三角形存在，将△BCE饶着点C顺时针旋转90°，就与△DCG重合
|
D |
|
A |
|
B |
|
C |
|
F |
|
E |
|
人行道 |
|
G |
|
30° |
|
D |
|
A |
|
B |
|
C |
|
F |
|
E |
|
人行道 |
|
G |
|
30° |
|
P |
|
Q |
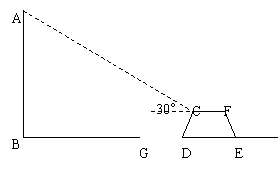
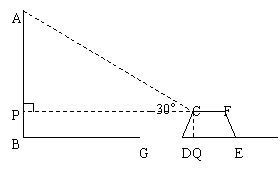27、不需要．理由是：
过点C作CP⊥AB于P，作CQ⊥DE于Q
由题意可得，DQ=1，
在Ｒt△CDQ中，∠CDQ=60°，
|
|
|
∵ 
= 
在Rt△APC中，PC=BQ=BD DQ=15，∠ACP=30°
AP=PCtan30°=15× 
∵BG=14-3=11，∴AB﹤BG ∴不需要封闭人行道．
28、(1) 由题意可得：
∴ 
(2) 设从2005年起，每年新增果树的增长率为x．
根据题意，得 
解这个方程，得 
∴2005年新增果树为 150×(1 20﹪)=180 (棵)
2006年通过“退耕还林”获得总收入为
29、（1）连接OˊP ∵O′P =O′F，∴∠O′PF=∠O′FP=∠α.
∴n° 2∠α=180° ∴∠α=90°－ 
（2）连结M′P，∵M′F是半圆O′的直径，
∴M′P⊥PF. 又∵FC⊥PF，∴FC//M′P.
若PC// M′F，则四边形M′PCF是平行四边形
∴PC= M′F=2FC，∠α=∠CPF=30°.
代入（1）中关系式得：
30°=90°－ 
30．(1)（3—x ,
（2）设rMPA的面积为S，在rMPA中，MA=3—x，MA边上的高为
其中，0≤x≤3.
∴S= 
∴S的最大值为
(3)延长NP交x轴于Q，则有PQ⊥OA
①若ＭＰ＝ＰＡ
∵ＰＱ⊥ＭＡ∴ＭＱ＝ＱＡ＝x.∴3x=3, ∴x=1
②若ＭＰ＝ＭＡ，则ＭＱ＝3—2x，ＰＱ=
在ＲtrＰＭＱ 中，∵ＰＭ2＝ＭＱ2＋ＰＱ2
∴(３—x) 2=(3—2x) 2 ( 
③若ＰＡ＝ＡＭ，∵ＰＡ＝ 
∴ 
综上所述，x=1，或x=
