| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
| 得分
| 阅卷人
| 复卷人
|
|
| | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
二、填空题(本大题共5小题,每小题3分,共15分.把正确答案直接填在题中的横线上)
15. x2 49 = (x 7)2.
16.计算:(π-3.14)0- ( ![]()
17.方程x2=4x的解是 .
 18.边长为2cm的正六边形面积等于 cm2.
18.边长为2cm的正六边形面积等于 cm2.
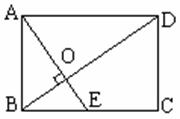
19.如图,在矩形ABCD中, 点E为边BC的中点, AE⊥BD,垂足为点O, 则 ![]()
三.解答题 (本大题共10小题,共93分)
得分
阅卷人
复卷人
20. (本题满分8分)
计算: ![]()
![]()
得分
阅卷人
复卷人
21. (本题满分8分)
化简:(1 ![]()
![]()
得分
阅卷人
复卷人
22.(本题满分8分)
已知:关于x的方程x2 4x a=0有两个实数根x1、x2,且2x1 -x2=7,求实数a的值.
得分
阅卷人
复卷人
23.(本题满分11分)
三明中学初三(1)班篮球队有10名队员,在一次投篮练习中,这10名队员各投篮50次的进球情况如下表:
进球数
42
32
26
20
19
18
15
14
人数
1
1
1
1
2
1
2
1
针对这次练习,请解答下列问题:
(1)求这10名队员进球数的平均数、中位数和众数;
(2)求这支球队整体投篮命中率;(投篮命中率= ![]()
(3)若队员小华的投篮命中率为40%,请你分析一下小华在这支球队中的投篮水平.
得分
阅卷人
复卷人
24.(本题满分8分)
如图,在一张圆桌(圆心为点O)的正上方点A处吊着一盏照明灯,实践证实:桌子边沿处的光的亮度与灯距离桌面的高度AO有关,且当sin∠ABO= ![]()
 (参考数据:
(参考数据: ![]()
![]()
![]()
得分
阅卷人
复卷人
25.(本题满分8分)
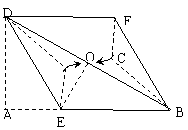
![]() 已知: ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
已知: ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
⑴求证:四边形ABCD是矩形;
|
O |
|
F |
|
D |
|
B |
|
E |
|
C |
|
· |
|
A |
 ⑵在四边形ABCD中,求
⑵在四边形ABCD中,求 得分
阅卷人
复卷人
26.(本题满分10分)
已知抛物线y=ax2 bx c过点A(0,2)、B( ![]()
![]()
⑴求a、b、c的值;
⑵①这条抛物线上纵坐标为 ![]()
②请写出: 函数值y随着x的增大而增大的x的一个范围 .
得分
阅卷人
复卷人
27.(本题满分8分)
如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.
⑴求证:CD是⊙O的切线;
|
A |
|
B |
|
D |
|
C |
|
· |
|
· |
|
E |
|
O |
|
P |
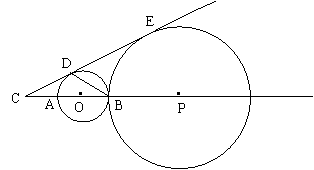 ⑵若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求
⑵若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求 得分
阅卷人
复卷人
28.(本题满分12分)
联想中学本学期前三周每周都组织初三年级学生进行一次体育活动,全年级400名学生每人每次都只参加球类或田径类中一个项目的活动.假设每次参加球类活动的学生中,下次将有20%改为参加田径类活动;同时每次参加田径类活动的学生中,下次将有30%改为参加球类活动.
⑴假如第一次与第二次参加球类活动的学生人数相等,那么第一次参加球类活动的学生应有多少名?
⑵假如第三次参加球类活动的学生不少于200名,那么第一次参加球类活动的学生最少有多少名?
得分
阅卷人
复卷人
29.(本题满分12分)
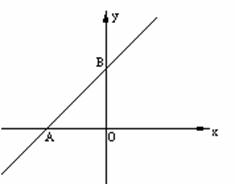
如图,已知直线y=x 4与x轴、y轴分别相交于点A、B,点M是线段AB(中点除外)上的动点,以点M为圆心,OM的长为半径作圆,与x轴、y轴分别相交于点C、D.
(1)设点M的横坐标为a,则点C的坐标为 ,点D的坐标为 (用含有a的代数式表示);
(2)求证:AC=BD;
(3)若过点D作直线AB的垂线,垂足为E.
①求证: AB=2ME;
②是否存在点M,使得AM=BE?若存在,求出点M的坐标;若不存在,请说明理由.

江苏省淮安市2005年初中毕业暨升学统一考试
数学试卷答案
一、选择题(每小题3分,共14小题,计42分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
答案
B
A
B
C
B
A
C
C
B
D
C
A
C
B
二、填空题(每小题3分,共5小题,计15分)
15.14x 16.-1 17.0或4 18.6 ![]()
![]()
三、解答题(共10题,合计93分)
20.(本题满分8分)解:原式= ![]()
=2 ![]()
= ![]()
21.(本题满分8分)解:原式= ![]()
= ![]()
= ![]()
22.(本题满分8分)解:∵ ![]()
![]()
![]()
∴ ![]()
由 ![]()
![]()
∴ ![]()
说明:(1)本题可利用求根公式进行求解,但要分类讨论;
(2)本题不写出△≥0(或不验证△≥0)不扣分。
23.(本题满分11分)解:(1)平均数= ![]()
=22 ………………………………2分
中位数=19 ……………………………………4分
众数有19和15………………………………6分
(2)投篮命中率= ![]()
(3)虽然小华的命中率为40%低于整体投篮命中率44%,但小华投50个球进了20个大于中位数19,事实上全队有6人低于这个水平,所以小华在这支队伍中的投篮水平中等以上。……………………………………………………………………………11分
说明:只要学生表达出用中位数衡量小华水平即可,答案可以是中等以上、较高等字眼。如学生没有用到中位数可扣一分。
|
B |
|
A |
|
O |
|
┌ |
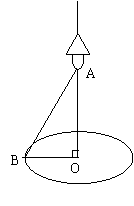 24.(本题满分8分)解法一:在Rt△OAB中,
24.(本题满分8分)解法一:在Rt△OAB中,
∵sin∠ABO= ![]()
![]()
即OA= ![]()
又OA2 OB2=AB2,且OB=60cm ……………………6分
解得OA=60 ![]()
答:高度OA约为85cm ………………………………………8分
解法二:∵OA⊥OB,sin∠ABO= ![]()
∴ 可设OA= ![]()
∵OA2 OB2=AB2,∴ ![]()
解得 ![]()
∴OA=60 ![]()
答:高度OA约为85cm ……………………………………………8分
注:其它解法参照给分。
例①先求cos∠ABO,再求tan∠ABO;②由sin∠ABO= ![]()
![]()
![]()
25.(本题满分8分)
(1)证实:连结OE
∵四边形ABCD是平行四边形,
∴DO=OB,……………………………………………………………1分
∵四边形DEBF是菱形,
∴DE=BE,……………………………………………………………2分
|
O |
|
F |
|
D |
|
B |
|
E |
|
C |
|
A |
 ∴EO⊥BD
∴EO⊥BD
∴∠DOE= 90°
即∠DAE= 90°…………………………………………4分
又四边形ABCD是平行四边形,
∴四边形ABCD是矩形………………………………………………5分
(2)解:∵四边形DEBF是菱形
∴∠FDB=∠EDB
又由题意知∠EDB=∠EDA
由(1)知四边形ABCD是矩形
∴∠ADF=90°,即∠FDB ∠EDB ∠ADE=90°
则∠ADB= 60°…………………………………………………………7分
∴在Rt△ADB中,有AD∶AB=1∶ ![]()
即 ![]()
说明:其他解法酌情给分
26.(本题满分10分)
(1)解:∵点B( ![]()
![]()
![]()
![]()
又抛物线 ![]()
∴ 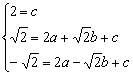
解得 ![]()
(2)① 2 ………………………………………………………8分
②x≤ ![]()
![]()
![]()
27.(本题满分8分)
(1)证实:连结OD、DA
∵AB是⊙O的直径,∴∠BDA=90°
又∠ABD=30°,∴AD= ![]()
又AC=AO,∴∠ODC=90°
∴CD切⊙O于点D……………………………………………………4分
(2)方法一:连结PE,由(1)知∠DAB=60°,又AD=AC
∴∠C=30°………………………………………………………………5分
又∵DE切⊙P于E,∴PE⊥CE
∴PE= ![]()
又PE=BP=R,CA=AO=OB= r
∴3r=R,即 ![]()
方法二:连结PE,
又∵DE切⊙P于E,∴PE⊥CE
∴OD∥PE ……………………………………………………………6分
∴ ![]()
![]()
即 ![]()
![]()
28.(本题满分12分)解:(1)设第一次参加球类活动的学生为x名,则第一次参加田径类活动的学生为(400-x)名
第二次参加球类活动的学生为x·(1-20%) (400-x)·30%
由题意得:x = x·(1-20%) (400-x)·30%……………………………3分
解之,得:x = 240 ……………………………………………………………………4分
(2)∵第二次参加球类活动的学生为x·(1-20%) (400-x)·30%= ![]()
∴第三次参加球类活动的学生为:
![]()
∴由 ![]()
又当x=80时,第二次、第三次参加球类活动与田径类活动的人数均为整数。
答:⑴第一次参加球类活动的学生应有240名;
⑵第一次参加球类活动的学生最少有80名 ……………………………………12分
29.⑴C(2a,0),…………………………………………………………………1分
D(0,2a 8)………………………………………………………………2分
⑵方法一:由题意得:A(-4,0),B(0,4)
-4<a<0,且a≠2,………………………………………………………………3分
① 当2a 8<4,即-4<a<-2时
AC=-4-2a,BD=4-(2a 8)=-4-2a
∴AC=BD……………………………………………………………………………5分
② 当2a 8>4,即-2<a<0时
同理可证:AC=BD
综上:AC=BD……………………………………………………………………………6分
方法二:①当点D在B、O之间时,
连CD,∵∠COD=90°
∴圆心M在CD上,………………………………………………………………3分
过点D作DF∥AB,
∵点M为CD中点,
∴MA为△CDF中位线,
∴AC=AF,…………………………………………………………………………4分
又DF∥AB,
∴ ![]()
而BO=AO
∴AF=BD
∴AC=BD……………………………………………………………………………5分
②点D在点B上方时,同理可证:AC=BD
综上:AC=BD…………………………………………………………………………6分
⑶方法一
①A(-4,0),B(0,4),D(0,2a 8),M(a,a 4),△BDE、△ABO均为等腰直角三角形,
E的纵坐标为a 6,∴ME= ![]()
![]()
![]()
AB=4 ![]()
∴AB=2ME…………………………………………………………………………9分
②AM= ![]()
![]()
![]()
![]()
∵AM=BE
又-4<a<0,且a≠2,
10 当-4<a<-2时
![]()
![]()
∴a=-3
M(-3,1)………………………………………………………………………11分
20 当-2<a<0时
![]()
![]()
∴a不存在………………………………………………………………………12分
方法二:
①当点D在B、O之间时,作MP⊥x轴于点P、MQ⊥y轴于点Q,取AB中点N,
在Rt△MNO与Rt△DEM中,MO=MD
∠MON=450-∠MOP
∠EMD=450-∠DMQ=450-∠OMQ=450-∠MOP
∴∠MON=∠EMD
∴Rt△MNO≌Rt△DEM………………………………………………………………7分
∴MN=ED=EB
∴AB=2NB=2(NE+EB)=2(NE+MN)=2ME…………………………8分
当点D在点B上方时,同理可证………………………………………………9分
②当点D在B、O之间时,
由①得MN=EB,
∴AM=NE ……………………………………………………………………10分
若AM=BE,则AM=MN=NE=EB= ![]()
![]()
∴M(-3,1)……………………………………………………………………11分
点D在点B上方时,不存在。…………………………………………………12分
注:(2)、(3)两问凡需要讨论而没有讨论的,每漏讨论一次扣1分。
![]() 恭贺你顺利完成答题,别忘了认真检查!
恭贺你顺利完成答题,别忘了认真检查!
| |