| |
|
[组图]中考数学全真模拟试卷
|
| 查询数中考复习的详细结果
|
|
一、填空题(每小题3分,共15分)
1、  是矩形
是矩形  的内接矩形,且
的内接矩形,且 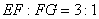 ,
,  ,则
,则 
2、某市初三年级举行以班为单位的基层数学团体赛,在各校预赛的基础上,每校选派一个班级中25名同学参加决赛,实验初中三(2)班、三(6)班为该校的候选班级,他们预赛的成绩如下: |
得分 |
50 |
60 |
70 |
80 |
90 |
100 | |
人数 |
三(2) |
4 |
5 |
10 |
8 |
14 |
9 | |
三(6) |
4 |
4 |
16 |
2 |
12 |
12 | |
已经算得两个班的平均分都是80分
①利用你学的统计知识,比较 班的实力更均衡些.
②你认为应派 班的25名同学参加决赛.
3、数轴上表示 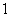 、
、 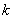 的对应点分别为
的对应点分别为  、
、  ,点
,点  关于点
关于点  的对称点
的对称点  所示的数是
所示的数是
4、在平面直角坐标系中,直线  与双曲线
与双曲线  只有一个交点,则
只有一个交点,则 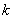 的值为
的值为

5、如图,圆木的横截面圆半径均为  ,则将这七根圆木用绳子扎住,每周所需绳子的长度为
,则将这七根圆木用绳子扎住,每周所需绳子的长度为
二、(共7分)
 如图, 如图,  是⊙
是⊙  的直径,
的直径,  ,垂足为
,垂足为  ,
,  是弦,交
是弦,交  和
和  于点
于点  、
、  .
.
①假如 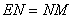 ,求证:
,求证:  .
.
②假如弦  交
交  于点
于点  ,且
,且  ,求证:
,求证:  .
.
三、(共8分)
已知关于  的方程
的方程 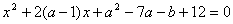 有两个相等的实数根,且满足
有两个相等的实数根,且满足  .
.
①利用根与系数的关系判定这两根的正负情况.
②若将  图象沿对称轴向下移动3个单位,写出顶点坐标和对称轴方程.
图象沿对称轴向下移动3个单位,写出顶点坐标和对称轴方程.
 四、(11分) 四、(11分)
如图所示, 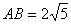 ,
,  ,
, 
①求过  、
、  、
、  三点的二次函数解析式.
三点的二次函数解析式.
②若  是
是  的中点,试判定点D在这条二次函数的图象上吗?并说明理由.
的中点,试判定点D在这条二次函数的图象上吗?并说明理由.
③若  随
随  的增大而减小,求
的增大而减小,求  的取值范围.
的取值范围.
五、(9分)
正方形  中,有一直径为
中,有一直径为  的半圆,
的半圆,  ,现有两点
,现有两点  、
、  ,分别从点
,分别从点  、点
、点  同时出发,点
同时出发,点  沿线段
沿线段  以
以 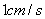 的速度向点
的速度向点  运动,点
运动,点  沿折线
沿折线  以
以  的速度向点
的速度向点  运动,设点
运动,设点  离开
离开  的时间为
的时间为 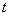 秒
秒
①当 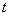 为何值时,线段
为何值时,线段  与
与  平行?
平行?
②设  ,当
,当 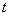 为何值时,
为何值时,  与半圆相切?
与半圆相切?
 ③当 ③当  时,设
时,设  与
与 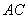 相交于点
相交于点 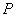 ,问点
,问点  、
、  运动时,点
运动时,点 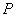 的位置是否发生变化?若变化,请说明理由;若不发生变化,请给予证实,并求
的位置是否发生变化?若变化,请说明理由;若不发生变化,请给予证实,并求  的值.
的值.
 
参考答案
一、1、  ;2、①二班②六班;3、
;2、①二班②六班;3、  ;4、
;4、  ;5、
;5、 
二、证实:①连结  ,
,
∵  是⊙
是⊙  的直径,∴
的直径,∴ 
∵  ,∴
,∴ 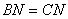 ,
, 
又 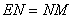 ,∴
,∴  △
△ 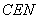 ≌
≌  △
△ 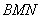
  ∴ ∴ 
又∵  ,∴
,∴  ,∴
,∴ 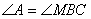
∴ 
又 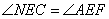
在△  和△
和△  中
中
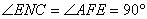
即 
②连结  、
、  、
、 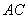
∵点  是
是  垂直平分线
垂直平分线  上一点,∴
上一点,∴ 
∵ 
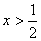  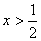 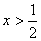 ∴ ∴  ,∴
,∴  ,∴
,∴ 
又 
∴△ 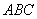 ≌△
≌△ 
∴ 
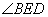 是公共角
是公共角
∴△  ∽△
∽△  ,
,
∴ 
∴ 
三、①解:由 
得  ,又
,又  得
得

设这个方程的解为  、
、  则
则

∴  、
、  均为正根
均为正根
② ∵ 
∴  可化为:
可化为:
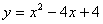 ,将此图象向下移动2个单位,得
,将此图象向下移动2个单位,得

顶点  ,对称轴为
,对称轴为 
四、解:①  ,
, 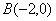 ,
, 
∴ 
②∵  是
是  的中点,∴
的中点,∴ 
∵ 
∴点D一在这条二次函数的图象上
③∵ 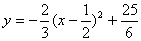 ,
,  开口向下
开口向下
∴当 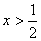 时,
时,  随
随  的增大而减小
的增大而减小
五、解:①点  离开点
离开点 
 秒,
秒,  ,
, 
要使  与
与  平行,则应
平行,则应 
∴  ,得
,得 
②  与半圆相切,作
与半圆相切,作 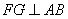 于
于 
在  △
△  中,∵
中,∵ 
∴ 
∴  (秒)
(秒)
③当  时,点
时,点 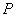 的位置不会发生变化
的位置不会发生变化
证实:  、
、  出发
出发  秒时,
秒时, 
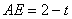 ,
, 
∴ 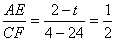
又∵  ,∴△
,∴△  ∽△
∽△ 
∴ 
因此,当  时,点
时,点 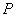 的位置与
的位置与  的取值无关,点
的取值无关,点  的位置不会发生变化。
的位置不会发生变化。
|