1．如图，已知⊙O1经过⊙O2的圆心O2，且与⊙O2相交于A、B两点，点C为弧AO2B上的一动点（不运动至A、B），连结AC，并延长交⊙O2于点P，连结BP、PC
|
| 。O2 |
|
| P |
|
| 。O1 |
|
| A |
|
| B |
|
| C |
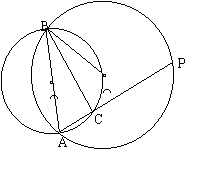（1）当点C在运动时，观察图中有哪些角的大小没有变化？
（2）请猜想△BCP的外形，并证实你的猜想
2．如图，已知AB是⊙O的直径，直线MN与⊙O相交于点E，F，AD⊥MN，垂足为D。
（1）求证：∠BAE=∠DAF
|
| 。O |
|
| E |
|
| D |
|
| A |
|
| B |
|
| N |
|
| F |
|
| M |
（2）若把直线MN向上平行移动，使之与AB相交，其他条件不变，请把变化后图形画出来，并指出∠BAE=∠DAF是否仍然相等（直接回答，不必证实）
|
| A |
|
| A1 |
|
| C1 |
|
| B1 |
|
| C1 |
|
| D |
|
| C |
|
| B |
|
| L |
3．如图，课本中曾要我们证实“已知平行四边形ABCD及形舛一直线L，AA1⊥L，BB1⊥L，CC1⊥L，DD1⊥L。求证：AA1 CC1=BB1 DD4．如图，AD是⊙O的直径，BC切⊙O于D，AB，AC交⊙O于E，F
（1）求证：AE·AB=AF·AC
|
| 。O |
|
| E |
|
| D |
|
| A |
|
| C |
|
| F |
|
| B |
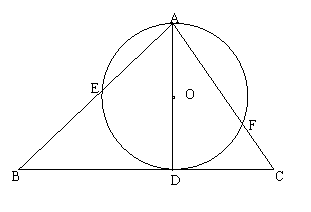（2）假如将直线BC向上或向下平移（与AD仍然垂直）且AB，AC交⊙O于E，F，则AE·AB=AF·AC还成立吗？
5．已知，如图，点C为线段AB上一点，△ACM，△CBN是等边三角形，则图（1）中存在结论AN=BM
（1）现将△ACM绕C点按逆时针方向旋转1800，使A点落在CB上，请在画出符合题意的图(2)
（2）在（2）中所得的图形中，结论“AN=BM”是否还成立？若成立，请证实；若不成立，请说明理由
|
| A |
|
| M |
|
| N |
|
| C |
|
| B |
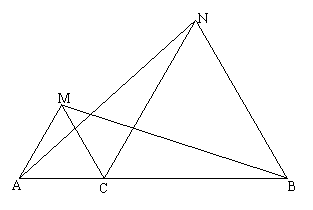（3）在（2）得到的图形中，设MA的延长线与BN相交于D点，请你判定△ABD与四边形MDNC的外形，并证实你的结论
|
| 。O2 |
|
| F |
|
| 。O1 |
|
| A |
|
| B |
|
| C |
|
| E |
|
| D |
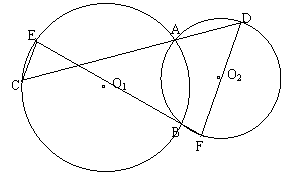
6．已知，如图，⊙O1和⊙O2相交于A、B，过点A的直线CD与⊙O1交于C，与⊙O2交于D，过点B的直线EF与⊙O1交于E，与⊙O2交于F，求证：CE∥DF
当上例的图形变为如下几个图时，仍有CE∥DF吗？如何证实？
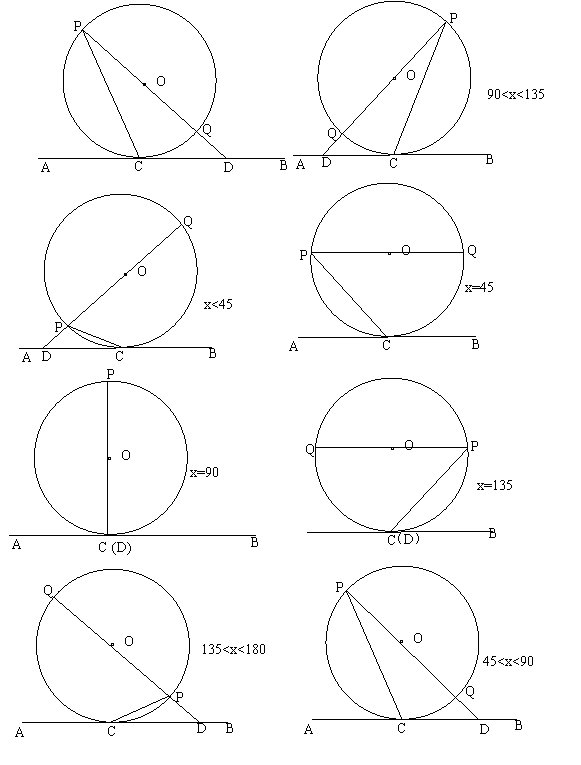
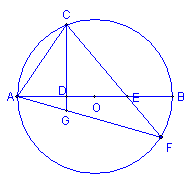
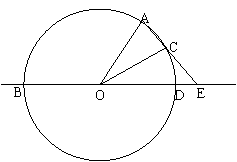
7．已知直线AB与⊙O相切于点C，P是⊙O上一点，直线PO与AB相交于D，设∠PCA=x，∠PDC=y，试探索y与x之间的数量关系。
|
| Q |
|
| D |
|
| 。O |
|
| A |
|
| B |
|
| C |
|
| P |
|
| Q |
|
| D |
|
| 。O |
|
| A |
|
| B |
|
| C |
|
| P |
|
| 。O |
|
| Q |
|
| A |
|
| B |
|
| C |
|
| P |
|
| P |
|
| Q |
|
| D |
|
| 。O |
|
| A |
|
| B |
|
| C |
|
| (D) |
|
| 。O |
|
| A |
|
| B |
|
| C |
|
| P |
|
| Q |
|
| D |
|
| 。O |
|
| A |
|
| B |
|
| C |
|
| P |
|
| Q |
|
| （D） |
|
| 。O |
|
| B |
|
| C |
|
| P |
|
| P |
|
| Q |
|
| D |
|
| 。O |
|
| A |
|
| B |
|
| C |
|
| 90<x<135 |
|
| 45<x<90 |
|
| 135<x<180 |
|
| x=135 |
|
| x=90 |
|
| x=45 |
|
| x<45 |
|
| 。 O |
|
| H |
|
| E |
|
| A |
|
| C |
|
| P |
|
| B |
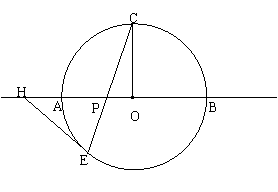8．如图，AB是⊙O的直径，P是线段AB上任意一点，已知OC⊥AB，若CP的延长线交⊙O于E点，EH切⊙O于E点，交直线AB于H点，问：线段EH和HP有怎样的大小关系？请证实你的结论。
|
| 。O1 |
|
| 。O1 |
|
| A |
|
| B |
|
| C |
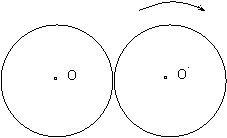
9．如图，⊙O1的半径O10．如图，两枚同样大的硬币，其中一个固定，另一个沿其四周滚动，滚动时，两枚硬币总是保持有一点
相接触（相外切），当滚动的硬币沿固定
的硬币四周滚动一圈，回到原来的位置
时，滚动的那个硬币自转的周数为（ ）
|
| 。O |
|
| 。O’ |
A、1 B、11．已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别是h1、h2、h3，△ABC的高为h，若点P在一边BC上，如图（1），此时h3=0，可得h1 h2 h3=h
|
| A |
|
| P |
|
| M |
|
| C |
|
| B |
|
| E |
|
| D |
|
| M |
|
| A |
|
| P |
|
| C |
|
| B |
|
| E |
|
| D |
|
| F |
|
| A |
|
| P |
|
| C |
|
| B |
|
| E |
|
| D |
|
| F |
|
| M |
|
| 如图（3） |
|
| 如图（2） |
|
| 如图（1） |
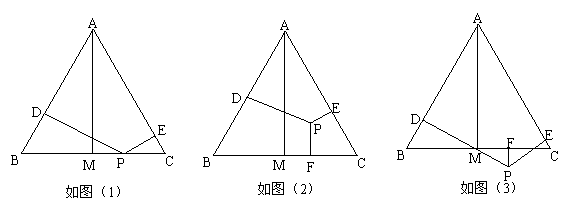请直接应用上述信息解决下列问题：
如图（2）当点P在△ABC内、如图（3），当点P在△ABC外这两种情况时，上述结论是否还成立？若成立，请给予证实；若不成立，则h1、h2、h3，与h之间又有怎样的关系；请写出你猜想，不需证实。
12．已知，AB⊙O的直径，P为AB延长线上的一个动点，过点P作⊙O的切线，设切点为C，
（1）当点P在AB延长线上的位置，如图1所示时，连结AC，作∠APC的平分线，交AC于点D，请你测量出∠CDP的度数，
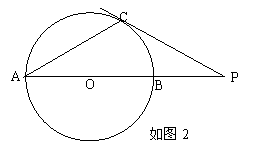
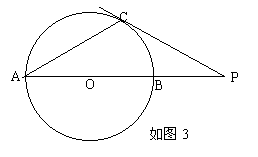
（2）当点P在AB延长线的位置如图2和图3所示时，连结AC，请你分别在这两个图中用尺规作出∠APC的平分线，设此角平分线交AC于点D，然后在这两个图中分别测量出∠CDP的度数；
|
| A |
|
| B |
|
| P |
|
| C |
|
| D |
|
| O |
|
| 如图1 |
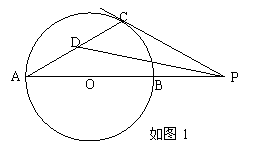猜想：∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？请对你的猜想加以证实，
|
| A |
|
| B |
|
| P |
|
| C |
|
| |
|
| O |
|
| 如图2 |
|
| A |
|
| B |
|
| P |
|
| C |
|
| |
|
| O |
|
| 如图3 |
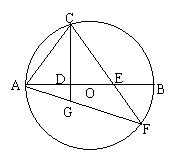
13．AB是⊙O的直径，C是⊙O上一点，连结AC，过点C作直线CD⊥AB于D（AD<DB），点E是DB上任意一点（点D、B除外），直线CE交⊙O于点F，连结AF与直线CD交于点G。
|
| A |
|
| B |
|
| F |
|
| C |
|
| D |
|
| O |
|
| E |
|
| G |
（1）求证：AC2=AG·AF；（2）若点E是AD（点A除外）上任意一点，上述结论是否仍然成立？
14．AB是⊙O的直径，C为圆上一动点，过点C作圆的切线交AB的延长线于P，∠CPA的角平分线交AC于点D，交CB于点E。
（1）请你观察图中的∠CAB，∠CDP，∠ACP，∠CPA，∠COP，∠CED，∠CBA中，哪些角的度数是固定不变的；
（2）求出这些固定不变的角的度数，并说明理由
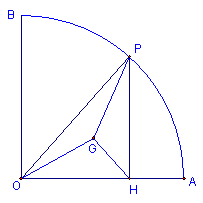
15．如图，在半径为6，圆心角为900的扇形OAB的弧AB上，有一个动点P，PH⊥OA，垂足为H，△OPH的重心为G，则当点P运动时，线段GO、GH=2，永远不变中，有无保持不变的线段，假如有，请指出这样的线段，并求出相应长度。
16．如图，正方形ABCD中，有一直径为BC的半圆，BC=
（1）设t= 
秒时，线段EF与BC有什么位置关系？
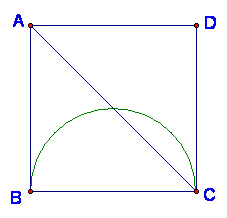（2）当1≤t＜2时,设EF与AC相交于点P，问点E、F运动进，点P的位置是否发生变化？若发生变化，请说明理由；若不发生变化，请证实，并求出AP：PC的值。
17．操作：将一把三角尺放在边长为4的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线 DC相交于点Q
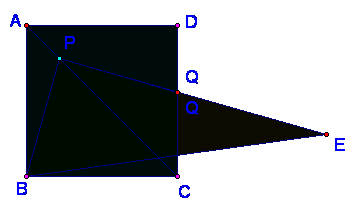探究：设A、P两点间的距离为x
（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证实你的结论
（2）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形?假如可能，指出所有可能的情况，并求出相应的x的值。
18．如图，直线AB经过⊙O的圆心,与⊙O相交于A、B两点，点C在⊙O上，且∠AOC=300,点E是直线AB上的一个动点（与点O不重合），直线EC交⊙O于D，则使DE=DO的点共有
A、1个 B、2个 C、3 个 D、4个
|
| A |
|
| D |
|
| B |
|
| O |
|
| C |
|
| E |
19．如图，已知AB为半圆O的直径，AP为过点A的半圆的切线，在AB弧上任取一点C（点C与A、B不重合），过点C作半圆的切线CD交AP于点D；过点C作CE⊥AB,垂足为E，连结BD，交CE于点F。
（1）当点C为AB弧的中点时，求证：CF=EF；
（2）当点C不是AB弧的中点时，试判定CF与EF的相等关系是否保持
|
| A |
|
| D |
|
| F |
|
| C |
|
| O（E） |
|
| B |
|
| P |
|
| D |
|
| A |
|
| F |
|
| C |
|
| 。O |
|
| B |
|
| P |
|
| E |
不变，并证实你的结论。
|
| D |
|
| A |
|
| B |
|
| 。 N |
|
| C |
|
| P |
|
| E |
|
| Q |
|
| M |
|
| 。O |
|
| A |
|
| B |
|
| 。 O1 |
|
| C |
|
| D |
|
| m |
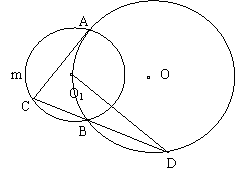20．已知，⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上，点C在⊙O1中优弧AmB上一动点，直线CB交⊙O2于D，问：在点C在运动过程中，图中的线段DO1与线段AC有怎样的位置关系？请证实你的猜想。
|
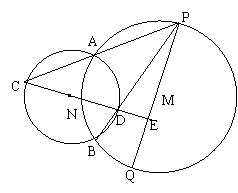
21．已知，如图，⊙M与⊙N相交于A、B两点，在⊙M上一动点P，PA的延长线交⊙N于C，PB交⊙N于D，PQ是⊙M的直径，CD和延长线交PQ于E，则在P点运动过程中，PD×PB与PE×PQ有相等关系吗？证实你的结论？
22．已知，如图，⊙O1与⊙O2相交于A、B两点，AC、BD分别是两圆的动弦，CD分别交两圆于E、F，则图中的∠CAE与∠DBF有怎样的大小关系？请证实你的猜想
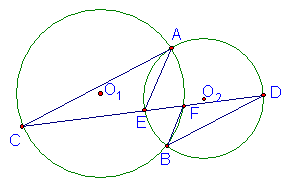
23．已知，如图，两圆外切于P，外公切线AB分别切两圆于A、B两点，过P的直线分别交两圆于C、D延长CA、DB相交于E，则线段CE与线段DE有怎样的位置关系？请证实你的结论。
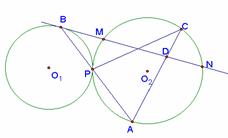24．已知⊙O1与⊙O2外切于点P，过点P的直线分别交⊙O1、⊙O2于点B、A，⊙O1的切线BN交⊙O2于点M、N，若D点在切线BN在运动时，则△APC与△ADB是否一定相似，请证实你的结论。
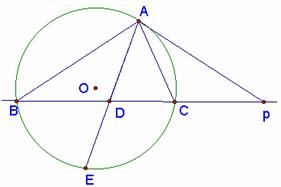
25．已知PA切⊙O于A点，直线CB交⊙O于C、B两点，D是直线BC上一个动点，且PD2=PB×PC，直线AD交⊙O于E点，若D点在直线BC上运动时，那么△ABE与△ADC是否一定相似？请你说明理由。
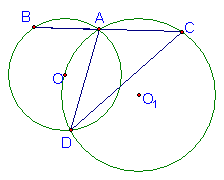26．已知AB是⊙O的弦，过A、O作⊙O1交BA延长线于C，交⊙O于D，若B点在⊙O上运动时，△BDC一定是等腰三角形吗？请说明你的理由。
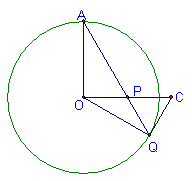27．已知，如图，⊙O的半径OA⊥OB，过A点的直线交OB于P，交⊙O于Q，过Q引⊙O的切线交OB延长线于C，且PQ=QC，当Q点在⊙O上运动时，线段OP与线段AP之间有怎样的等量关系？请证实你的结论。
28．已知两圆外切于P点，点A在⊙O上一动点，AC是过P点的割线，交⊙O1于C，BC切⊙O1于C，过O点作直线AB交BC于B，当动点A在⊙O上运动时，线段AB与线段BC有怎样的位置关系？请证实你的结论。
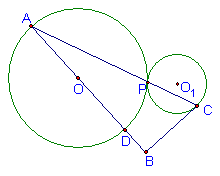
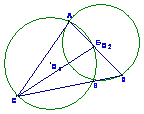29．已知，如图，⊙O1与⊙O2交于A、B两点，C点是⊙O1上一动点，若⊙O1的弦AC切⊙O2于A，连结CB交⊙O2于D，连结AD交⊙O1于E，问△ACE是什么三角形？请证实你的结论。
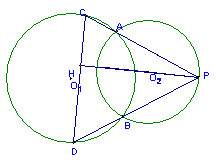30．已知，如图，⊙O1与⊙O2交于A，B两点，P是⊙O2上一点，连结PA，PB分别交⊙O1于C，D，则当P点在⊙O2上运动时，直线PO2与直线CD有怎样的位置关系，请证实你的猜想。
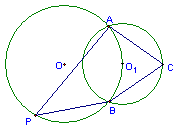31．已知，如图，⊙O经过⊙O1的圆心，两圆相交于A、B两点，点C在⊙O上运动，点P在⊙O1上运动时，∠P与∠C有什么数量大小关系？请证实你的结论。
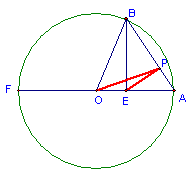32．如图，已知：在⊙O中，B为圆上一动点，BE⊥OA半径（或其延长线），EP⊥AB于P点，请你猜想OP2 EP2是否为定值，若圆的半径为R，则OP2 EP2的值为多少？（用R来表示）
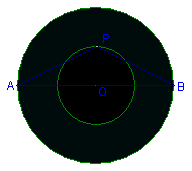33．如图，已知，AB是两同心圆的大圆的直径，P为小圆的一动点，请你猜想PA2 PB2是否为定值，(不必讲理由)若两圆的半径分别R和r，则PA2 PB2的值为多少？（用R和r来表示）
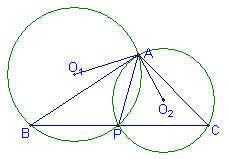
34．如图，已知，△ABC的一边BC上一动点P，则△ABP和△ACP的外接圆的半径之比是否为定值？为什么？
35．如图，已知，Rt△ABC中，∠A=900，内切圆⊙O切AB、BC、AC于E、D、F，外接圆半径为R，内切圆半径为r，问当A点在运动过程中，AB AC是否保持不变，并求当R=4，r=3时，求AB AC的值。
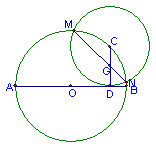36．如图，已知AB是⊙O的直径，C是⊙O上的一动点，CD⊥AB于D，⊙C以CD为半径且交⊙O于M、N，CD交MN于G，问当C点在⊙O上运动时，CG与DG有什么等量关系，请证实你的结论。
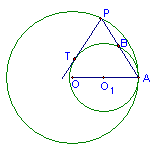37．如图，已知：⊙O与⊙O1内切于A，P为⊙O上一动点，PT与⊙O1切于T，PA交⊙O1于B，问PA2：PT2是否为定值，若两半径之比为2：1，则 
等于多少？
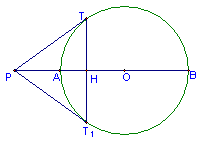38．P为圆外一点，已知：P为⊙O外一动点，切线PT、PT1，过圆心O割线PB交TT1于H，交⊙O于A、B，请问当P点运动时， 
是否为定值，这个定值为多少？
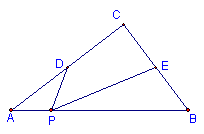39．如图，在Rt△ABC中，∠C=900，AC=3，BC=4，D、E分别是AC和BC上的中点，而P点在AB上运动，问四边形CAPE的面积是否保持不变，若保持不变，请你求出它的面积。
40．如图，AB是⊙O的直径， C是弧AB的中点，E、F两点同时从点C出发以相同的速度分别向A、B两点运动，试在直径AB上找一点使得这一点到E和F两点的距离和最小，若AB=
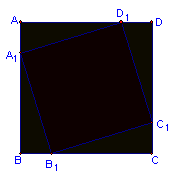41．正方形ABCD中，四个点A1、B1、C1、D1分别从A、B、C、D、出发以相同的速度向B1、C1、D1 、A1运动，问在运动过程中，(1)四边形A1B
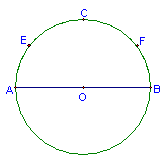
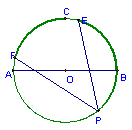42. 已知⊙O中，AB是⊙O的直径，C是弧AB的中点，点E、F分别从B、C两点向点C和点A运动，运动速度相同，点P在另一半圆弧上运动，问在运动过程中，∠EPF的角度是否变化？
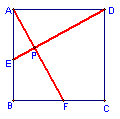43．如图，已知正方形ABCD中E、F从点A和点B两点同时出发分别向点B和点C运动，速度相同，则在运动过程中，线段AF和线段DE有怎样的位置和大小关系，请证实你的结论。
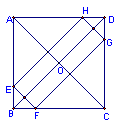44．如图，正方形ABCD中，E、F两点从点B同时分别向A、C两点运动，速度相同；G、H两点从点D同时分别向C、A两点运动，速度相同。则在运动过程中，（1）四边形EFGH的外形如何，是否保持不变；（2）四边形EFGH的周长是否保持不变；（3）若正方形的周长是
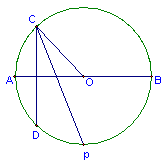45．如图，已知AB是⊙O的直径，点C在⊙O上运动（不与A、B两点重合）作弦CD⊥AB，并作∠DCO的平分线交⊙O于点P，在点C的运动过程中，点P位置是否保持不变，请证实你的结论。
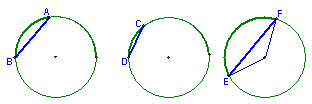
46．如图，在三个等圆上各有一条劣弧 
， 
，和 
，假如 
，那么AB CD与EF的大小关系是（ ）
A、AB CD=EF B、AB CD>EF C、AB CD<EF D、不能确定
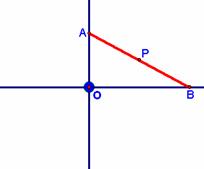47.如图，已知两条互相垂直的直线L1和L2相交于点O，一条固定长度的线段AB两端点A点和B点分别在直线L1和L2上运动，问：在运动过程中，线段AB的中点的轨迹是什么外形？
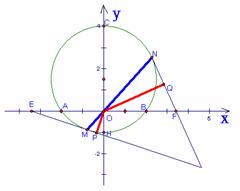48．已知：在直角坐标系中，x轴与⊙D交于A、B两点﹝A左B右﹞，圆心D在y轴正半轴上，⊙D与y轴交于C、H两点﹝C点在正半轴，H点在负半轴﹞，OB=OA=2，OC=4，过坐标原点O任作弦MN交圆于M、N，分别过M、N作⊙D的切线EM、NF﹝E点在x轴的负半轴，F点在x轴的正半轴﹞，过O作OP⊥EM于P，OQ⊥FN于Q，当MN沿⊙O运动时，问： 
的值是否变化？如不变化，那么它的值是多少？假如我们把问题改为求 
，则结论如何？
49．已知在梯形ABCD中，AD∥BC，AD＜BC，且AD=5，AB＝DC=2，若P为线段AD上的一动点，满足∠P=∠A。在P点运动过程中，∠P的一边交BC于E点，交线段CD或其延长线于点Q。
问题一：△ABP与△DPQ是否一定相似，为什么？
问题二：当点Q与点C重合时，AP的长是多少？
问题三：当点Q在线段CD上时，AP长取值范围是什么？
问题四：当点Q在线段CD的延长线上时，AP长的取值范围是什么？
问题五：当CE=1时，CE的长是多少？
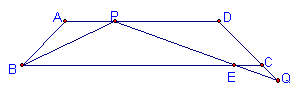
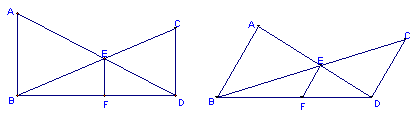
50．已知：AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证实 
成立（不要求考生证实）.若将垂线改为斜交， AB∥CD，AD，BC相交于点E，过点E作EF∥AB，交BD于点F，则：（1） 
还成立吗？假如成立，请给出证实；假如不成立，请说明理由；（2）请找出S△ABD，S△BED和S△BDC间的关系式，并给出证实.
 |
