| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
第Ⅱ卷(非选择题 共90分) 二.填空题(共6小题,每小题3分,计18分) 11.5×(-4.8) 12.分解因式:a3-2a2b+ab2=__a(a-b)2________。
 13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6, 13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,
sinA=
14.根据图中所给的数据,求得避雷针CD的长约为 __4.86______m(结果精确的到0.01m)。 (可用计算器求,也可用下列参考数据求: sin43°≈0.6802,sin40°≈0.6428,cos43°≈0.7341, cos40°≈0.7660,tan43°≈0.9325,tan40°≈0.8391)
 15.用7根火柴棒首尾顺次连接摆成一个三角形, 15.用7根火柴棒首尾顺次连接摆成一个三角形,
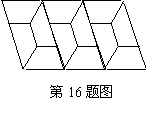
能摆成不同的三角形的个数为_2____ 16.右图是用12个全等的等腰梯形镶嵌成的图形, 这个图形中等腰梯形的上底长与下底长的比是1:2。 三、解答题(共9小题,计72分。解答应写出过程) 17.(本题满分5分)计算:(a2+3)(a-2)-a(a2-2a-2)。 解:(a2+3)(a-2)-a(a2-2a-2) =a3-2a2+3a-6-a3+2a2+2a………………………………………(3分)
 =5a-6…………………………………………………………………(5分) =5a-6…………………………………………………………………(5分)
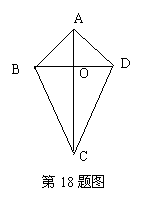
18.(本题满分6分) 如图,四边形ABCD中,AC垂直平分BD于点O。 (1) 图中有多少对全等三角形?请把它们都写出来; (2) 任选(1)中的一对全等三角形加以证实。 解:(1)图中有三对全等三角形:△AOB≌△AOD, △COB≌△COD,△ABC≌△ADC。………………(3分) (2) 证实△ABC≌△ADC。 证实:∵AC垂直平分BD, ∴AB=AD,CB=CD。……………………………………(5分) 又∵AC=AC,∴△ABC≌△ADC。……………(6分) 19.(本题满分7分) 已知: x1、x2是关于x的方程x2+(2a-1)x+a2=0的两个实数根 且(x1+2)(x2+2)=11,求a的值。 解:∵x1、x2是方程x2+(2a-1)x+a2=0的两个实数根, ∴x1+x2=1-2a,x1﹒x2=a2………………………………………(2分) ∵(x1+2)(x2+2)=11, ∴x1x2+2(x1+x2)+4=11……………………………………(3分) ∴a2+2(1-2a)-7=0,即a2-4a-5=0。 解得a=-1,或a=5。…………………………………………(5分) 又∵Δ=(2a-1)2-4a2=1-4a≥0, ∴a≤ ∴a=5不合题意,舍去。 ∴a=-1…………………………………………………………(7分) 20(本题满分8分) 为了了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班50名学生进行了调查,有关数据如下表:
| 每周做家务的时间(小时)
| 0
| 1
| 1.5
| 2
| 2.5
| 3
| 3.5
| 4
| 人数(人)
| 2
| 2
| 6
| 8
| 12
| 13
| 4
| 3 |
根据上表中的数据,回答下列问题:
(1) 该班学生每周做家务劳动的平均时间是多少小时?
(2) 这组数据的中位数、众数分别是多少?
(3) 请你根据(1)、(2)的结果,用一句话谈谈自己的感受。
解:(1)该班学生每周做家务劳动的平均时间为
![]()
答:该班学生每周做家务劳动的平均时间为2.44小时。……………(5分)
(2)这组数据的中位数是2.5(小时),众数是3(小时)。………(7分)
(4) 评分说明:只要叙述内容与上述数据有关或与做家务劳动有关,并且态度积极即可。………………………………………………(8分)
21.(本题满分8分)
某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册)
5000
8000
10000
15000
……
成本y(元)
28500
36000
41000
53500
……
(1) 经过对上表中数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2) 假如出版社投入成本48000元,那么能印该读物多少册?
解:(1)设所求一次函数的解析式为y=kx+b,……………………(1分)
则 ![]()
解得k= ![]()
∴所求的函数关系式为y= ![]()
(2)∵48000= ![]()
∴x=12800。……………………………………………………(7分)
答:能印该读物12800册。………………………………………(8分)
22.(本题满分8分)
阅读:我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图①.
观察图①可以得出:直线=1与直线y=2x+1的交点P的坐标(1,3)就是方程组 ![]()
![]()
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图③。
|
P(1,3) |
|
O |
|
x |
|
y |
|
3 |
|
第22题图① |
|
l |
|
x=1 |
|
y=2x 1 |
|
O |
|
x |
|
y |
|
第22题图② |
|
l |
|
x=1 |
|
O |
|
x |
|
y |
|
第22题图③ |
|
l |
|
y=2x 1 |
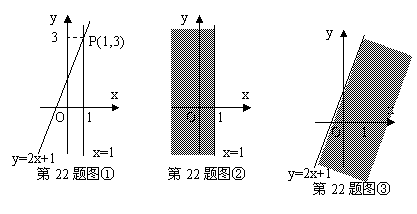
回答下列问题:
(1)
|
x |
|
y |
|
O |
|
第22题图 |
|
y=-2x 2 |
|
x=-2 |
|
P |
|
l |
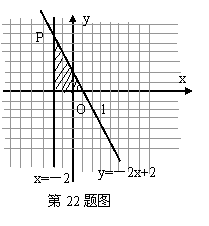 在直角坐标系(图④)中,用作图象的方法求出方程组
在直角坐标系(图④)中,用作图象的方法求出方程组 (2) 用阴影表示 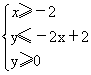
所围成的区域。
解:(1)如图所示,
在坐标系中分别作出直线x=-2和直线y=-2x+2,……(2分)
这两条直线的交点是P(-2,6)。(4分)
则 ![]()
![]()
(3) 如阴影所示。……………………………………………………(8分)
23.(本题满分8分)
如图,PC切⊙O于点C,过圆心的割线PAB交⊙O于A、B两点,BE⊥PE,垂足为E,BE交⊙O于点D,F是PC上一点,且PF=AF,FA的延长线交⊙O于点G。求证:(1)∠FGD=2∠PBC;
(2) ![]()
证实:(1)连结OC。……………………………………………………(1分)
∵PC切⊙O于点C,
∴OC⊥PC。
∵BE⊥PE,
∴OC∥BE。……………………………………………………(2分)
∴∠POC=∠PBE。
|
G |
|
A |
|
B |
|
C |
|
D |
|
E |
|
F |
|
O |
|
P |
|
第23题图 |
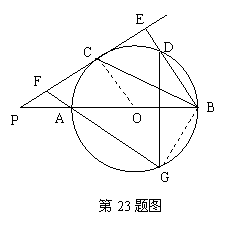 又∵∠PBE=∠FGD,
又∵∠PBE=∠FGD,
∴∠POC=∠FGD。……………………(3分)
∵∠POC=2∠PBC,
∴∠FGD=2∠PBC。……………………(4分)
(3) 连结BG。
∵AB是的直径,
∴∠AGB=90°。
又∵OC⊥PC,
∴∠PCO=90°,∴∠AGB=∠PCO。……………(5分)
∵FP=FA,
∴∠FPA=∠PAF=∠BAG。……………………(6分)
∴△PCO∽△AGB。……………………(7分)
∴ ![]()
24.(本题满分10分)
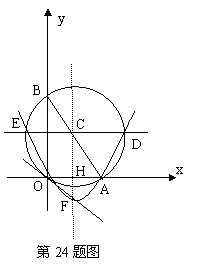
如图,在直角坐标系中,⊙C过原点O,交x轴于点A(2,0),交y轴于点B(0, ![]()
(1) 求圆心的坐标;
(2) 抛物线y=ax2+bx+c过O、A两点,且顶点在正比例函数
y=- ![]()
(3) 过圆心C作平行于x轴的直线DE,交⊙C于D、E两点,试判定D、E两点是否在(2)中的抛物线上;
(4) 若(2)中的抛物线上存在点P(x0,y0),满足∠APB为钝角,求x0的取值范围。
解:(1)∵⊙C经过原点O,
∴AB为⊙C的直径。
∴C为AB的中点。
过点C作CH垂直x轴于点H,则有CH= ![]()
![]()
OH= ![]()
∴圆心C的坐标为(1, ![]()
(2)∵抛物线过O、A两点,∴抛物线的对称轴为x=1。
∵抛物线的顶点在直线y=- ![]()
∴顶点坐标为(1,- ![]()
把这三点的坐标代入抛物线抛物线y=ax2+bx+c,得
|
A |
|
B |
|
C |
|
D |
|
E |
|
F |
|
O |
|
H |
|
第24题图 |
|
x |
|
y |
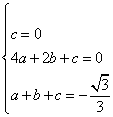
解得 
∴抛物线的解析式为 ![]()
(3)∵OA=2,OB=2 ![]()
∴ ![]()
即⊙C的半径r=2。∴D(3, ![]()
![]()
代入 ![]()
(4)∵AB为直径,
∴当抛物线上的点P在⊙C的内部时,满足∠APB为钝角。
∴-1<x0<0,或2<x0<3。………………………………(10分)
25.(本题满分12分)
已知:直线a∥b,P、Q是直线a上的两点,M、N是直线b上两点。
(1)
|
P |
|
Q |
|
M |
|
N |
|
a |
|
b |
|
第25题图① |
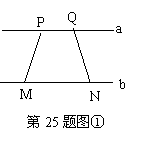 如图①,线段PM、QN夹在平行
如图①,线段PM、QN夹在平行
直线a和b之间,四边形PMNQ
为等腰梯形,其两腰PM=QN。
请你参照图①,在图②中画出异
于图①的一种图形,使夹在平行
直线a和b之间的两条线段相等。
(2) 我们继续探究,发现用两条平行直
|
a |
|
b |
|
第25题图② |
 线a、b去截一些我们学过的图形,
线a、b去截一些我们学过的图形,
会有两条“曲线段相等”(曲线上两
点和它们之间的部分叫做“曲线段”。
把经过全等变换后能重合的两条曲线
段叫做“曲线段相等”)。
请你在图③中画出一种图形,使夹在
平行直线a和b之间的两条曲线段相等。
|
a |
|
b |
|
第25题图③ |
|
P |
|
Q |
|
M |
|
N |
|
a |
|
b |
|
第25题图④ |
|
S1 |
|
S2 |
|
S3 |
|
S4 |
|
n |
|
m |
 |
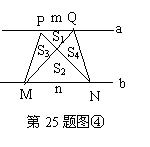 | ||
(3) 如图④,若梯形PMNQ是一块绿化地,梯形的上底PQ=m,下底MN=n,且m<n。现计划把价格不同的两种花草种植在S1、S2、S3、S4四块地里,使得价格相同的花草不相邻。为了节省费用,园艺师应选择哪两块地种植价格较便宜的花草?请说明理由。
|
P |
|
Q |
|
M |
|
N |
|
a |
|
b |
|
图例: |
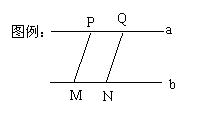 解:(1)(只要图符合题意给3分)
解:(1)(只要图符合题意给3分)
|
P |
|
(Q) |
|
M |
|
N |
|
a |
|
b |
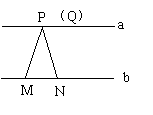 |
或 (3分)
(2)(只要图符合题意给3分)
|
P |
|
Q |
|
M |
|
N |
|
a |
|
b |
|
图例: |
|
P |
|
Q |
|
M |
|
N |
|
a |
|
b |
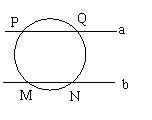 | |||
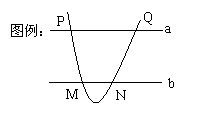 | |||
或 (6分)
解:(3)∵△PMN和△QMN同底等高。
∴S△PMN=S△QMN。∴S3 S2=S4 S2.∴S3=S4。………………(7分)
∵△POQ∽△NOM, ∴ ![]()
∴S2= ![]()
∵ ![]()
![]()
∴ ![]()
![]()
∵m>n,
∴ ![]()
故园艺师应选择S1和S2两块地种植价格较便宜的花草,因为这两块的的面积之和大于另两块地的面积之和。…………………(12分)
| |