中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
(1)请完成下表：
|
| 平均数
| 中位数
| 众数
| 方差
| 85分以上的频率
| 甲
| 84
|
| 84
| 14．4
| 0．3
| 乙
| 84
| 84
|
| 34
| |
(2)利用以上信息，请从三个不同的角度对甲、乙两名同学的成绩进行分析．
21.(本题满分10分)
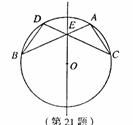
如图，在⊙O中，弦AB与DC相交于点E，AB=CD．
(1)求证：△AEC≌△DEB；
(2)点B与点C关于直线OE对称吗?试说明理由．
22.(本题满分10分)
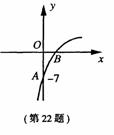
已知抛物线 
所示，抛物的顶点在第一象限，且经过点A(0，-7)和点B.
(1)求a的取值范围；
(2)若OA=2OB，求抛物线的解析式．
23．(本题满分12分)
某水果批发市场香蕉的价格如下表：
购买香蕉数
(千克)
不超过
20千克
20千克以上但不超过40千克
40千克以上
每千克价格
6元
5元
4元
张强两次共购买香蕉50千克(第二次多于第一次)，共付款264元，请问张强第一次、第二次分别购买香蕉多少千克?
24．(本题满分12分)
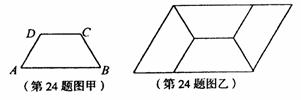
如图甲，四边形ABCD是等腰梯形，AB∥DC．由4个这样的等腰梯形可以拼出图乙所示的平行四边形。
(1)求四边形ABCD四个内角的度数；
(2)试探究四边形ABCD四条边之间存在的等量关系，并说明理由；
(3)现有图甲中的等腰梯形若干个，利用它们你能拼出一个菱形吗?若能，请你画出大致的示意图．
25．(本题满分12分)
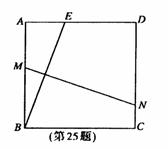
如图，在正方形ABCD中，AB=2，E是AD边上一点(点E与点A，D不重合)．BE的垂直平分线交AB于M，交DC于N．
(1)设AE=x，四边形ADNM的面积为S，写出S关于x的函数关系式；
(2)当AE为何值时，四边形ADNM的面积最大?最大值是多少?
二OO五年中等学校招生考试
数学参考答案及评分标准(新课标卷)
一、选择题：本大题共12小题，1～8题每小题选对得4分，9～12题每小题选对得
5分，选错、不选或选出的答案超过一个均记零分.
ACBBC BDBCC DD
二、填空题：本大题共6小题，共24分，每小题填对得4分.
17．-4 18．40
三、解答题：以下各题仅给出一种解(证)法，其它解(证)法，可参照本标准酌情赋分.
19．解：原式 
当 
20．解：（1）
|
项 |
|
目 |
|
学 |
|
生 |
平均数
中位数
众数
方差
85分以上的频率
甲
84
84
84
14.4
0.3
乙
84
84
90
34
0.5
……………4分
(2)甲成绩的众数是84，乙成绩的众数是90，从两人成绩的众数看，乙的成绩较好. …………………………………………………………………6分
甲成绩的方差是14.4，乙成绩的方差是34，从成绩的方差看，甲的成绩相对稳定． ………………………………………………………………8分
甲成绩、乙成绩的中位数、平均数都是84，但从85分以上的频率看，乙的成绩较好． ……………………………………………………10分
21．解：(1)∵AB=CD， ∴ 
∴ 
∴ 
在△AEC与△DEB中，∠ACE=∠DBE，∠AEC=∠DEB，
∴△AEC≌△DEB ……………………………………………5分
(2)点B与点C关于直线OE对称. ……………………………7分
理由如下：
由(1)得BE＝CE， ∴点E在直线BC的中垂线上.
连结BO，CO．
∵BO＝CO， ∴点O在线段BC的中垂线上.
∴直线EO是线段BC的中垂线.
∴点B与点C关于直线OE对称． ………………………10分
22．解：(1)由图可知，b=-7. …………………………………1分
故抛物线为y=(1-a)x2 8x-7又抛物线的顶点在第一象限，开口向下，所以抛物线与x轴有两个不同的交点．
∴ 
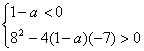
即a的取值范围是
(2)设B(x1，o)，由OA=20B，得7=2x1，，即 
由于
∴ 
∴ 
故所求所抛物线解析式为 
23．解：设张强第一次购买香蕉x千克，第二次购买香蕉y千克．由题意，得
0<x<25． ………………………………………………………………2分
① 当0<x≤20，y≤40时，由题意，得
② 当0<x≤20，y>40时，由题意，得
③ 当20<x<25时，25<y<30．此时张强用去的款项为
5x 5y=5(x y)=5×50=250<264(不合题意，舍去) ……………11分
综合①②③可知，张强第一次购买香蕉14千克，第二次购买香蕉36千克. …12分
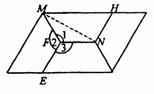
24．解：(1)如图，∠1=∠2=∠3，∠1 ∠2 ∠3=360°，
所以3∠1=360°，即∠1=120°．
所以梯形的上底角均为120°，下底角均为60° …3分
(2)由于EF既是梯形的腰，又是梯形的上底，所以梯形的腰
等于上底． 连接MN，则∠FMN=∠FNM=30°．
从而∠HMN=30°，∠HNM=90°．所以NH= 
因此，梯形的上底等于下底的一半，且等于腰长． …………………7分
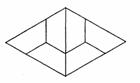(3)能拼出菱形． ……………………………………………………………8分
如图：(拼法不唯一)
………12分
25．解：(1)连接ME，设MN交BE于P，根据题意，得
MB=ME，MN⊥BE． ………………………………………………2分
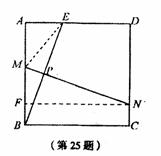过N作AB的垂线交AB于F，在Rt△MBP和Rt△MNF中，
∠MBP ∠BMN=90°，∠FNM ∠BMN=90°，
∴∠MBP=∠MNF．
又AB=FN，
∴Rt△EBA≌Rt△MNF，故MF=AE=x.
在Rt△AME中，AE=x，ME=MB=2-AM，
∴(2-AM)2=x2 AM2．
解得AM= 
所以四边形ADNM的面积
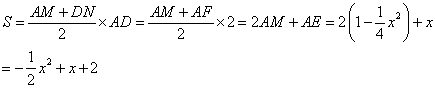
即所求关系式为 
(2) 
∴当AE=x=1时，四边形ADNM的面积S的值最大,最大值是 
| |
(C)计算机随机产生的两位数是偶数 (D)星期天是晴天
4.下列图形经过折叠不能围
7.如图，甲为四等分数字转盘，乙为三等分数字转盘．同时自由
是( )
