| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
对于同一个
x 这些特性反映在图象上就是将 由于 4.抛物线的顶点坐标、对称轴方程的求法有2种:一种是将
= = = 所以顶点是(-3,2),对称轴是 另一种是直接套用公式.顶点 5.抛物线的顶点是
0 x
0 x ③若
0 x y
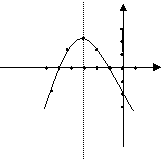
0 所以,(1) (2) (3) 判定抛物线与 再例如求 6.求解二次函数的图象,应先求出顶点坐标,对称轴方程,然后按照对称性列表、描点、连线. 如:解出 解:顶点坐标是(-3,2),对称轴是 列表,得:
|
| …
| -6
| -5
| -4
| -3
| -2
| -1
| 0
|
| …
| -
| 0
|
| 2
|
| 0
|
|
描点、连线,得:
![]()
x
![]()
三、练习
1.填空题:
⑴将 ![]()
⑵将 ![]()
⑶函数 ![]()
![]()
⑷ ![]()
![]()
⑸将 ![]()
![]()
⑹抛物线 ![]()
![]()
![]()
⑺二次函数 ![]()
![]()
![]()
⑻ ![]()
⑼ ![]()
![]()
![]()
⑽已知二次函数 ![]()
⑾抛物线 ![]()
![]()
![]()
⑿已知二次函数 ![]()
![]()
![]()
![]()
⒀已知二次函数 ![]()
![]()
S四边形OBDC=______
2.选择题:
①假如 ![]()
![]()
A. 4 B. 0 C. 6 D. -6
② 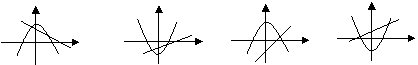
![]()
![]()
![]()
![]()
y y y y
0 x 0 x 0 x 0 x
A. B. C. D.
③二次函数 ![]()
![]()
A. ![]()
![]()
C. ![]()
![]()
④抛物线 ![]()
![]()
A.(4,0) B.( ![]()
![]()
![]()
⑤要使关于 ![]()
![]()
![]()
A. 0 B. –1 C. 1 D. 2
3.解答题:
已知二次函数 ![]()
![]()
![]()
![]()
![]()
![]()
求:①此函数的解析式,并画出图象.
②在 ![]()
求出D的值;若不存在,说明理由.
四、练习答案:
1.填空题:
⑴ ![]()
![]()
![]()
![]()
⑶(-3,1) ⑷下 二 ⑸ ![]()
![]()
⑹(3,0)和(- ![]()
![]()
![]()
⑻ ![]()
![]()
⑾A(-1,0) B(3,0) P点(0,3)和(2,3) (提示:AB=4 设P( ![]()
![]()
![]()
![]()
![]()
![]()
⑿ ![]()
![]()
⒀ ![]()
![]()
![]()
![]()
![]()
2.选择题:
①B ②D ③C ④C ⑤C
3.解答题:
由题意得 ![]()
![]()
![]()
![]()
![]()
由②得: ![]()
![]()
![]()
将 ![]()
![]()
![]()
![]()
![]()
![]()
所以 ![]()
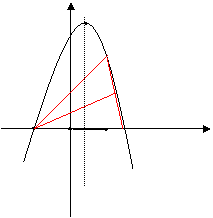 设D(
设D( ![]()
则S△ABC= ![]()
S△DBC= ![]()
![]()
∴ ![]()
将 ![]()
![]()
∴D ![]()
| |