| |
|
[组图]嘉善县初中毕业、升学模拟考试
|
| 查询数中考复习的详细结果
|
|
嘉善县初中毕业、升学模拟考试
数 学
试 题 卷
考生须知:
1.全卷分卷一和卷二两部分,其中卷一为选择题卷;卷二为非选择题卷,卷一的答案必须做在答题卡上;卷二的答案必须做在卷二答题卷的相应位置上.
2.全卷满分为150分.考试时间为100分钟.
3.请用钢笔或圆珠笔在卷二答题卷密封区内填写县(市、区)、学校、姓名和准考证号.
4.请在答题卡上先填写姓名和准考证号,再用铅笔将准考证号和科目对应的括号或方框涂黑.
卷 一
说明:本卷有一大题,共48分.请用铅笔在答题卡上将所选项对应字母的方框涂黑、涂满.
一、选择题(本题有12小题,每小题4分,共48分,每小题只有一个选项是正确的,不选、多选、错选均不给分)
1. 计算 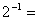
(A)-2 (B) 2 (C) 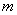 (D)
(D) 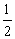
2.1天24小时共有86400秒,用科学记数法可表示为(保留两位有效数字)
(A) 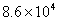 秒 (B)
秒 (B)  秒 (C)
秒 (C) 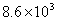 秒 (D)
秒 (D) 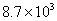 秒
秒
3.若点A(a,b)在第二象限,则点B(a,-b)在
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4. 已知  ,
, 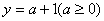 ,则
,则  和
和  的关系是
的关系是
(A)  (B)
(B)  (C)
(C) 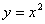 (D)
(D) 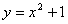
5.已知D、E分别为△ABC中AB、AC边上的点,直线DE将△ABC的面积分成两部分,其中一部分为x,另一部分为y.当△ABC的面积不变时,则y和x的函数图象为
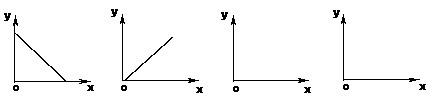
(A) (B) (C) (D)
6.已知圆锥的侧面展开图是一个半圆,则母线与高的夹角是
(A)15° (B)30° (C)45° (D)60°
7.图象经过点(2,3)的反比例函数的解析式是
(A) 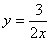 (B)
(B) 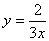 (C)
(C) 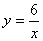 (D)
(D) 
8.方程组 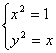 的解有
的解有
(A)1组 (B)2组 (C)3组 (D)4组
 9.如图,已知DE∥BC,AD∶DB=3∶2,则DE∶BC的值是 9.如图,已知DE∥BC,AD∶DB=3∶2,则DE∶BC的值是
(A) 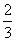 (B)
(B) 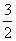 (C)
(C) 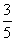 (D)
(D) 
10.下列轴对称图形中,对称轴条数最多的图形是
(A)等腰三角形 (B)正三角形 (C)菱形 (D)等腰梯形
  11.以下各图放置的小正方形的边长都相同,分别以小正方形的顶点为顶点画三角形,则与△ABC相似的三角形图形为 11.以下各图放置的小正方形的边长都相同,分别以小正方形的顶点为顶点画三角形,则与△ABC相似的三角形图形为
(A) (B) (C) (D)
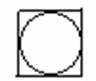 12.如图,在三个同样大小的正方形中,分别画一个内切圆,面积为 12.如图,在三个同样大小的正方形中,分别画一个内切圆,面积为  (图甲所示);画四个半径相等的两两外切、且与正方形各边都相切的圆,这四个圆的面积之和为
(图甲所示);画四个半径相等的两两外切、且与正方形各边都相切的圆,这四个圆的面积之和为 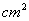 (图乙所示);画九个半径相等相互外切、且与正方形各边都相切的圆,这九个圆的面积之和为
(图乙所示);画九个半径相等相互外切、且与正方形各边都相切的圆,这九个圆的面积之和为 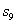 (图丙所示);则
(图丙所示);则  、
、 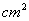 和
和 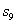 的大小关系是
的大小关系是
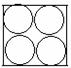 
图甲 图乙 图丙
(A)  最大 (B)
最大 (B) 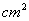 最大 (C)
最大 (C) 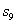 最大 (D)一样大
最大 (D)一样大
卷 二
说明:本卷有二大题,共102分,请用钢笔或圆珠笔将答案做在“卷二答题卷”的相应位置上,做在试题卷上无效.
二、填空题(本题有6小题,每小题5分,共30分)
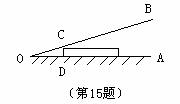 13.当 13.当 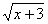 取最小值时,
取最小值时,  = ▲ .
= ▲ .
 14.如图,已知半圆的直径AB=3cm,P是AB上的 点, 14.如图,已知半圆的直径AB=3cm,P是AB上的 点,
则AP·PB的最大值
=_ ▲ 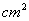 .
.
15.如图,已知sin∠AOB = 0.1,OC=1.2厘米,则小矩形木条的厚度
CD = ▲ 厘米.
16.已知圆柱形茶杯的高为12厘米,底面直径为5厘米,将长为20厘米的筷子沿底面放入杯中,筷子露在杯子口外的长度是  厘米,则
厘米,则  的取值范围是 ▲ 厘米.
的取值范围是 ▲ 厘米.
17.某单位要制作一批宣传材料,甲公司提出:每份材料收费20元,另收3000元设计费,乙公司提出:每份材料收费30元,不收设计费.什么情况下选择甲公司比较合算? _ _ ▲ .
18.用边长为1cm的小正方形搭如下的塔状图形,则第n次所搭图形的周长
 是 _ ▲ cm(用含n的代数式表示). 是 _ ▲ cm(用含n的代数式表示).
 ··· ···
第1次 第2次 第3次 第4次 ···
三、解答题(本题有7小题,共72分)以下各小题必须写出解答过程.
19.(本小题8分)
计算: 
20.(本小题8分)
已知关于  的一元二次方程
的一元二次方程 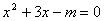 有实数根.
有实数根.
⑴ 求 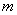 的取值范围;
的取值范围;
 ⑵ 若 两个实数根分别为 ⑵ 若 两个实数根分别为  ,且
,且 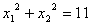 ,求
,求 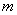 的值.
的值.
21.(本小题8分)
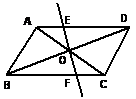
如图,已知O是  □ABCD的对角线的交点,过点O作直线分别与AD和BC相交于点E、F,求证:OE=OF.
□ABCD的对角线的交点,过点O作直线分别与AD和BC相交于点E、F,求证:OE=OF.
22.(本小题10分)
 如图,一小球从斜坡O点处抛出,球的抛出路线可用二次函数 如图,一小球从斜坡O点处抛出,球的抛出路线可用二次函数  的图象表示, 斜坡可以用一次函数
的图象表示, 斜坡可以用一次函数  的图象表示.
的图象表示.
⑴ 求小球到达最高点的坐标;
⑵ 若小球的落点是A,求点A的坐标.
23.(本小题12分)
某商场经营一批进价为2元一件的小商品,在销售中发现此商品的日销售单价
 (元)与日销售量
(元)与日销售量  (件)之间有如下的一次函数关系:
(件)之间有如下的一次函数关系:
|

|
3 |
5 |
7 |
…… | |

|
18 |
14 |
10 |
…… | |
⑴ 求  与
与  的函数解析式; ⑵ 求日销售额P(元)的最大值.
的函数解析式; ⑵ 求日销售额P(元)的最大值.

24.(本小题12分)
如图,已知正五边形ABCDE的边长为2 .
⑴ 计算正五边形ABCDE的一个内角 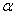 的度数;
的度数;
⑵ 若AE和CD的延长线相交于点O,计算DO的长.
25.(本小题14分).
如图,射线OA⊥射线OB,半径 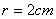 的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM
的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM 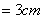 .设OP=
.设OP= 
 ,OQ=
,OQ= 
 .
.
⑴ 求  、
、  所满足的关系式,并写出
所满足的关系式,并写出  的取值范围 ;
的取值范围 ;
⑵ 当△MOP为等腰三角形时,求相应  的值;
的值;
⑶ 是否存在大于2的实数  ,使△MQO∽△OMP?若存在,求相应
,使△MQO∽△OMP?若存在,求相应  的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

2004年初中毕业、升学模拟考试评分意见
数 学
一、选择题:(每小题4分,共48分)
BACDAB CBCBAD
二、填空题:(每小题5分,共30分)
13. -3 14. 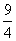 15. 0.12
15. 0.12
16. 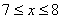 17. 答案不唯一 18.
17. 答案不唯一 18. 
三、解答题:(共72分)
19. 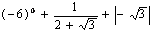
= 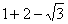 --------------------------------------------------------------------------------6分
--------------------------------------------------------------------------------6分
= 3 ----------------------------------------------------------------------------------------2分
20.⑴由△= 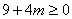 ------------------------------------------------------------------------1分
------------------------------------------------------------------------1分
得 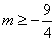 ----------------------------------------------------------------------------2分
----------------------------------------------------------------------------2分
⑵∵ 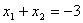
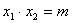 ---------------------------------------------------------2分
---------------------------------------------------------2分
 ----------------------------------------------------1分
----------------------------------------------------1分
∴ 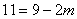 -------------------------------------------------------------------------1分
-------------------------------------------------------------------------1分
∴  ---------------------------------------------------------------------------------1分
---------------------------------------------------------------------------------1分
21.∵ ABCD ∴AO=OC------------------------------------------------------------------1分
AD∥, ∠EAO=∠FOC ---------------------------------------------------------2分
∵∠AOE=∠COF------------------------------------------------------------------------ 1分
∴△ AOE≌△COF --------------------------------------------------------------------- 2分
∴OE=OF -------------------------------------------------------------------------------- 2分
22. ⑴最高点(顶点)的横坐标为4, ------------------------------------------------------- 2分
最高点(顶点)的纵坐标为8, ------------------------------------------------------ 2分
⑵由 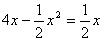 -------------------------------------------------------------- 2分
-------------------------------------------------------------- 2分
得 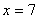 或
或 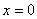 (舍去) --------------------------------------------------------- 2分
(舍去) --------------------------------------------------------- 2分
∴点A的横坐标为7 ----------------------------------------------------------------1分
点A的纵坐标为 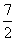 ---------------------------------------------------------------1分
---------------------------------------------------------------1分
23.⑴ 设 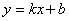 --------------------------------------------------------------------- 2分
--------------------------------------------------------------------- 2分
∴ 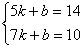 -------------------------------------------------------------------- 2分
-------------------------------------------------------------------- 2分
∴  ,
,  , 即
, 即 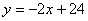 ---------------------------------------- 2分
---------------------------------------- 2分
⑵ 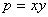 --------------------------------------------------------------------------- 2分
--------------------------------------------------------------------------- 2分
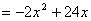 ----------------------------------------------------------------- 2分
----------------------------------------------------------------- 2分
∴ 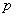 的最大值为72 ---------------------------------------------------------------- 2分
的最大值为72 ---------------------------------------------------------------- 2分
24.⑴ ∵五边形的内角和=540°----------------------------------------------------- 2分
∴ 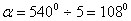 ------------------------------------------------------- 2分
------------------------------------------------------- 2分
⑵连结CE,由∠CDE=108°,CD = DE 得∠ECD =∠ CED = 360°-------1分
在四边形ABCD中, ∠O = 360°-108°×3 = 360 -----------------------1分
又∵∠OED =∠ ODE,∴OD = OE---------------------------------------------1分
∴ CE = OE = OD-------
由 △CED工∽ △COE ------------------------------------------------------------1分
得 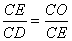 ---------------------------------------------------------------------1分
---------------------------------------------------------------------1分
∴  ----------------------------------------------------------------1分
----------------------------------------------------------------1分
∴ 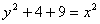 即
即 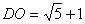 -----------------------------------------------1分
-----------------------------------------------1分
25.⑴ 作MC⊥OA,得 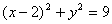 --------------------------------------2分
--------------------------------------2分
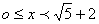 -----------------------------------------------------------------2分
-----------------------------------------------------------------2分
⑵当MQ = MP时,  = 4 ------------------------------------------------------1分
= 4 ------------------------------------------------------1分
当PM = PO时,  = 3 -------------------------------------------------------1分
= 3 -------------------------------------------------------1分
当OM = OP时, 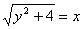 ,解得
,解得 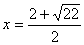 ----------------2分
----------------2分
⑶ ∵ 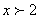 , ∴只有当∠OMP = 90°时,△MQD工∽ △MOP -----1分
, ∴只有当∠OMP = 90°时,△MQD工∽ △MOP -----1分
由  得
得 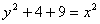 ----------------------------2分
----------------------------2分
∴  ----------------------------------------------------------------1分
----------------------------------------------------------------1分
∵ 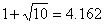 ,
,  -------------------------------1分
-------------------------------1分
即存在  ,使△MQO∽ △MOP ---------------------------------1分
,使△MQO∽ △MOP ---------------------------------1分
(其他解法参照给分)
|