| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
(1)由观察所得 ▲ 班的标准差较大; (2)若两班共有60人及格,问参加者最少获 ▲ 分 才可以及格。 21.(本小题8分)已知下面方格纸中的每一个小方格是边长为1的正方形, (1) 请你在图1中任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并用字母标注线段和写出线段长度。 (2) 图2中A、B两点是在小方格的顶点上,位置如图所示,请在图2中某小方格的顶点上确定一点C,连结AC、BC、AB,使三角形ABC的面积为2个平方单位,(画出图形即可)
学家大会的会标图案,其中四边形ABCD和EFGH都是正方形。 求证:ΔABF≌ΔDAE
23.(本小题12分)某单位计划在“五·一”劳动节组织员工到H地旅游 ,人数估计在10—25人之间,甲、乙两旅行社的服务质量相同,且组织到H地旅游的价格都是每人200元,该单位联系时,甲旅行社表示可给予每位旅客七五折优惠;乙旅行社表示可免去一位游客的旅游费用,其余游客八折优惠,问该单位应怎样选择,使其支付的旅游总费用较少?
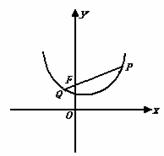
25.(本小题14分)已知点P是抛物线y = (1) 猜想d1、d2的大小关系,并证实; (2) 若直线PF交此抛物线于另一点Q(异于P点)。 ① 判定以PQ为直径的圆与x 轴的位置关系,并说明理由; ② 以PQ为直径的圆与y 轴的交点为A、B,若OA·OB=1,求直线PQ对应的函数解析式。
数 学 卷二答题卷
| 题 号
| 二
| 三
| 卷二总分
| 13—18
| 19
| 20
| 21
| 22
| 23
| 24
| 25
| 得 分
|
|
|
|
|
|
|
|
| | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
本卷有二大题,共102分。
二、填空题(本题有6小题,每小题5分,共30分)
13、 14、____________________
15、 16、____________________
17、 18、____________________
三、解答题(本题有7小题,共72分)
19、(本小题8分)计算:8 ÷(-2)3 ( ![]()
![]()
20、(本小题8分)A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0,1,2,3,4,5,6,7,8,9分这几种不同的分值中的一种,测试结果A班的成绩如下表所示,B班的成绩如右图所示。
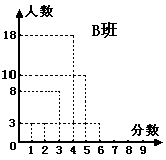 A班
A班
分数
0
1
2
3
4
5
6
7
8
9
人数
1
3
5
7
6
8
6
4
3
2
(1)由观察所得 班的标准差较大;
(2)若两班共有60人及格,问参加者最少获
分才可以及格。
21、(本小题8分)已知下面方格纸中的每一个小方格是边长为1的正方形,
(3) 请你在图1中任意连结这些小正方形的若干个顶点,可得到一些线段,试分别画出一条长度是有理数的线段和一条长度是无理数的线段,并用字母标注线段和写出线段长度。
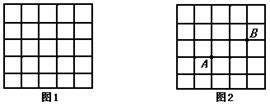 图2中A、B两点是在小方格的顶点上,位置如图所示,请在图2中某小方格的顶点上确定一点C,连结AC、BC、AB,使三角形ABC的面积为2个平方单位,(画出图形即可)有理数的线段是
图2中A、B两点是在小方格的顶点上,位置如图所示,请在图2中某小方格的顶点上确定一点C,连结AC、BC、AB,使三角形ABC的面积为2个平方单位,(画出图形即可)有理数的线段是
长度是 无理数的线段是
长度是
|
B |
|
A |
|
C |
|
D |
|
E |
|
F |
|
G |
|
H |
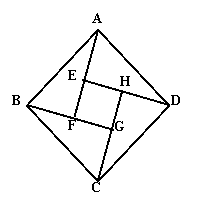 22、(本小题10分)
22、(本小题10分)
如图是2002年8月在北京召开的第24届国际数学家大会的会标图案,其中四边形ABCD和EFGH都是正方形。
求证:ΔABF≌ΔDAE
23、(本小题12分)某单位计划在“五·一”劳动节组织员工到H地旅游 ,人数估计在10—25人之间,甲、乙两旅行社的服务质量相同,且组织到H地旅游的价格都是每人200元,该单位联系时,甲旅行社表示可给予每位旅客七五折优惠;乙旅行社表示可免去一位游客的旅游费用,其余游客八折优惠,问该单位应怎样选择,使其支付的旅游总费用较少?
24、(本小题12分)如图, ⊙C的半径为6,圆心C的坐标为(0,9),点P在x轴的正半轴上移动,过点P作⊙C的切线,切点分别为A、B,连接AB交y轴于点D,当点P在x轴的正半轴上移动时,D点的位置是否改变?若不变,求出D点的坐标;若变化,设OP=x,请你用含x的代数式来表示D点坐标。
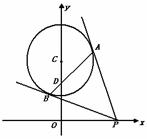
25、(本小题14分)已知点P是抛物线y = ![]()
距离为d1, 点P与点F(0,2)的距离为d2。
(3) 猜想d1、d2的大小关系,并证实;
(4) 若直线PF交此抛物线于另一点Q(异于P点)。
① 判定以PQ为直径的圆与x 轴的位置关系,并说明理由;
② 以PQ为直径的圆与y 轴的交点为A、B,若OA·OB=1,求直线PQ对应的函数解析式。
| |