|
中考专题突破试验与操作题专训
典例剖析
1.问题:要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面。
操作:
方案一:在图1中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图2中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图)。
探究:
⑴求方案一中圆锥底面的半径;
⑵求方案二中半圆圆心为O,圆柱两个底面圆心为O1、O2,圆锥底面的圆心为O3,试判定以
O1、O2、O3、O为顶点的四边形是什么样的非凡四边形,并加以证实。


2.在一服装厂里有大量外形为等腰直角三角形的边角布料(如图7).现找出其中的一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同外形的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其它边相切.请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径)

3.(A)右图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用  …表示;角度用
…表示;角度用 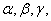 …表示);
…表示);
(3)根据你测量的数据,计算A、B两棵树间的距离.
(B)现有树12棵,把它栽成三排,要求每排恰好为5棵,如右图所示就是一种符合条件的栽法.请你再给出三种不同的栽法(画出图形即可).

4.李大爷有一个边长为a的正方形鱼塘(图-1),鱼塘四个角的顶点A、B、C、D上各有一棵大树.现在李大爷想把原来的鱼塘扩建成一个圆形或正方形鱼塘(原鱼塘四周的面积足够大),又不想把树挖掉(四棵大树要在新建鱼塘的边沿上).
(1)若按圆形设计,利用(图-1)画出你所设计的圆形鱼塘示意图,并求出网形鱼塘的面积;
(2)若按正方形设计,利用(图-2)画出你所设计的正方形鱼塘示意图;
(3)你在(2)所设计的正方形鱼塘中,有无最大面积?为什么?
(4)李大爷想使新建鱼塘面积最大,你认为新建鱼塘的最大面积是多少?
 5.如图,把边长为 5.如图,把边长为  的正方形剪成四个全等的直角三角形。请用这四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拼法仿照图中实际大小画在方格纸内(方格为
的正方形剪成四个全等的直角三角形。请用这四个直角三角形拼成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拼法仿照图中实际大小画在方格纸内(方格为 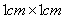 )
)
(1)不是正方形的菱形(一个) (2)不是正方形的矩形(一个)
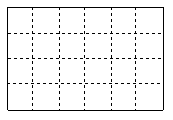 
(3)梯形(一个) (4)不是矩形和菱形的平行四边形(一个)
(5)不是梯形和平行四边形的凸四边形(一个)
6.在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下方案(如图①所示):
(1)在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN= 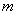 ;
;
(3)量出测倾器的高度AC=  .
.
根据上述测量数据,即可求出旗杆的高度MN.
假如测量工具不变,请仿照上述过程,设计一个测量某小山高度(如图②)的方案:
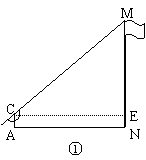
 (1)在图②中,画出你测量小山高度MN的示意图(标上适当字母); (1)在图②中,画出你测量小山高度MN的示意图(标上适当字母);
(2)写出你设计的方案.
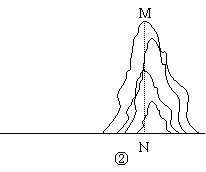
7.如图,有一木制圆形脸谱工艺品, 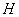 、
、  两点为脸谱的耳朵,打算在工艺品反面两耳连线中点
两点为脸谱的耳朵,打算在工艺品反面两耳连线中点  处打一小孔.现在只有一块无刻度单位的直角三角板(斜边大于工艺品的直径),请你用两种不同的方法确定点
处打一小孔.现在只有一块无刻度单位的直角三角板(斜边大于工艺品的直径),请你用两种不同的方法确定点  的位置(画出图形表示),并且分别说明理由.
的位置(画出图形表示),并且分别说明理由.

理由是:
巩固练习:
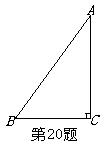 1、(长春2004) 如图,Rt△ABC中,∠C=90°. 1、(长春2004) 如图,Rt△ABC中,∠C=90°.
(1)请以AC所在的直线为对称轴,画出与△ABC成轴对称的图形;
(2)所得图形与原图形组成的图形是等腰三角形吗?请说明理由.
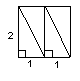
2、(河北2004) 图2是一个经过改造的台球桌面的示意图,图中四个角上的阴影
 部分分别表示四个入球孔.假如一个球按图中所示的方向被击出 部分分别表示四个入球孔.假如一个球按图中所示的方向被击出
(球可以经过多次反射),那么该球最后将落入的球袋是
A.1 号袋 B.2 号袋
C.3 号袋 D.4 号袋
3、(河北2004) 扑克牌游戏
小明背对小亮,让小亮按下列四个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步 从左边一堆拿出两张,放入中间一堆;
 第三步 从右边一堆拿出一张,放入中间一堆; 第三步 从右边一堆拿出一张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 .
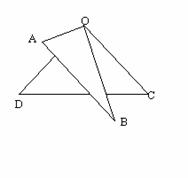
4、(黑龙江2004)如图,将一副三角板叠放在一起,使直角的顶点重合与O,则∠AOC ∠DOB=____________
5、(黑龙江2004) 在劳技课上,老师请同学门在一张长为17厘米,宽为16厘米的长方形纸上,剪下一个腰长为10厘米的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上)。请你帮助同学们计算剪下的等腰三角形的面积.
6、(南通2004) 如图,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:⑴用直线分割;⑵每个部分内各有一个景点;⑶各部分的面积相等。(可用铅笔画,只要求画图正确,不写画法)

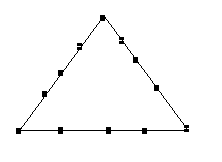 7、(潍坊2004)现有树12棵,把它栽成三排,要求每排恰好为5棵,如右图所示就是一种符合条件的栽法.请你再给出三种不同的栽法(画出图形即可). 7、(潍坊2004)现有树12棵,把它栽成三排,要求每排恰好为5棵,如右图所示就是一种符合条件的栽法.请你再给出三种不同的栽法(画出图形即可).
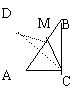 8、(哈尔滨2004) 如图,在RtΔABC,∠ACB=900, ∠A<∠B,CM是斜边AB的中线,将ΔACM沿直线CM折叠,点A落在点C处,假如CD恰好与AB垂直,那么∠A等于 度. 8、(哈尔滨2004) 如图,在RtΔABC,∠ACB=900, ∠A<∠B,CM是斜边AB的中线,将ΔACM沿直线CM折叠,点A落在点C处,假如CD恰好与AB垂直,那么∠A等于 度.
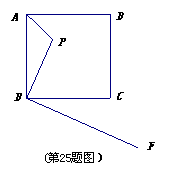 9、(宁波2004)如图,已知P是边长为4 的正方形ABCD内一点,且PB=3,BP⊥BF垂足为B,请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似(请注重:全等图形是相似图形的特例) 9、(宁波2004)如图,已知P是边长为4 的正方形ABCD内一点,且PB=3,BP⊥BF垂足为B,请在射线BF上找一点M,使以点B、M、C为顶点的三角形与△ABP相似(请注重:全等图形是相似图形的特例)
10、(陕西2004) 如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 个不同的四边形.

|