|
第二学期初三中考适应性独立练习卷(一)数学题卷
时间:100分钟 满分:120分
一、填空题(本题共102题,每小题3分共30分)
1.用科学记数法表示0.000528为________(保留两个有效数字)。
 2.四边形ABCD中,已知AB∥CD,若再增加一个条件________可判定四边形ABCD为平行四边形。 2.四边形ABCD中,已知AB∥CD,若再增加一个条件________可判定四边形ABCD为平行四边形。
3.已知等腰三角形的二边分别为7和8,则它的周长________。
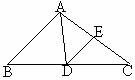
4.如图△ABC中,DE为AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长________cm。
5.二次函数y=2(x-1)2 7的顶点坐标________。
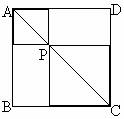
6.在⊙O中,弦AB=8cm,弦心距OC=3cm,则该圆的半径为________cm。
7.已知二次函数y=ax2 bx c的图象经过(1,-2),则a b c的值是________。
 8.全等三角形的对应边相等,对应角相等的题设是:____________________结论是:_______________________________________________。 8.全等三角形的对应边相等,对应角相等的题设是:____________________结论是:_______________________________________________。
9.如图,在正方形ABCD中AB=1,点p为对角线AC上的一点,分别以PA、PC为对角线作正方形,则二个小正方形的周长的和是________。
10.已知关于x,y的方程组  的解都是正数,化简3-|m| |2-m|=________。
的解都是正数,化简3-|m| |2-m|=________。
二、选择题(每小题3分,共30分,请选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)。
( )11、下列函数中,二次函数是
A、y= 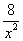 1 B、y=
1 B、y=  C、y=8x 1 D、y=8x2 1
C、y=8x 1 D、y=8x2 1
 ( )12、如图所示,已知在△ABC中,AB的中垂线交AC于点E,交AB于D,若AE=2 ( )12、如图所示,已知在△ABC中,AB的中垂线交AC于点E,交AB于D,若AE=2 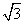 ,则B、E两点间的距离是
,则B、E两点间的距离是
A、4 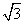 B、2
B、2 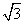 C、
C、 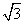 D、
D、 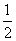
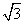
( )13、下列说法正确的是
A、每一个命题都有逆命题 B、每个定理都有逆定理
 C、假命题的逆命题一定是假命题 D、真命题的逆命题一定是真命题 C、假命题的逆命题一定是假命题 D、真命题的逆命题一定是真命题
( )14、如图所示,已知△ABC中,AB=BC,BD为角平分线,DE⊥AB于E,DF⊥BC于F,则下列四个结论:①BD上任一点到点A、点C的距离相等;②BD上任一点到AB、BC的距离相等;③AD=CD,BD⊥AC;④∠ADE=∠CDF,其中正确的个数有
A、1个 B、2个
C、3个 D、4个
 ( )15、分式 ( )15、分式 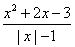 的值为0,则x的取值为
的值为0,则x的取值为
A、x=-3 B、x=3
C、x=-3或x=1 D、x=3或x=-1
( )16、如图,y=ax2 bx c的图像,则a,b,c,b2-4ac这四个数值中小于零的个数有
A、1个 B、2个 C、3个 D、4个
( )17、小红、小明、小芳在一起做游戏时,需要确定游戏的先后顺序。他们约定用“剪子、包袱、锤子”的方式确定。问在一个回合中三个都都出包袱的概率是。
A、 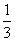 B、
B、 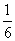 C、
C、 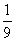 D、
D、 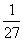
 ( )18、如图,已知D、E是△ABC中BC边上的二点,且AD=AE,要使△ABE≌△ACD,下列各项中,不能作为补充条件的是 ( )18、如图,已知D、E是△ABC中BC边上的二点,且AD=AE,要使△ABE≌△ACD,下列各项中,不能作为补充条件的是
A、AB=AC B、∠AEB=∠ADC
C、BD=CE D、∠B=∠C
( )19、函数y=ax2-bx c的图像过点(-1,0),则 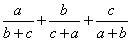 的值是
的值是
A、-3 B、3 C、 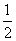 D、-
D、- 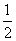
 ( )20、如图,BC是半圆O的直径,过点D作⊙O切线AD,BA⊥DA交于点A,BA交半圆于E,已知BC=10,AD=4,那么直线CE与点O为圆心,2.5为半径的圆的位置关系是 ( )20、如图,BC是半圆O的直径,过点D作⊙O切线AD,BA⊥DA交于点A,BA交半圆于E,已知BC=10,AD=4,那么直线CE与点O为圆心,2.5为半径的圆的位置关系是
A、相交 B、相切
C、相离 D、不能确定
三、解答题(共60分)
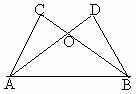 21、(本小题8分)如图,∠CAB=∠DBA,AC=BD,求证:①AD=BC,②S△AOC=S△BOD 21、(本小题8分)如图,∠CAB=∠DBA,AC=BD,求证:①AD=BC,②S△AOC=S△BOD
22、(本题8分)已知关于x的一元二次方程x3 3x 1-m=0.
(1)请选取一个你喜爱的m的值,使方程有两个不相等的实数根,并说明它的正确性;
(2)设x1,x2是(1)中你所得的方程的两个根,求x1x2 x1 x2的值。
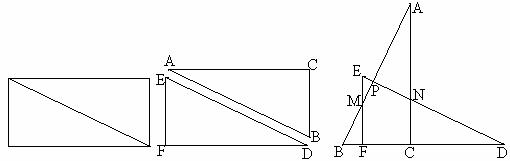
23、(本小题10分)将一张矩形纸片沿对角线剪开,得到两张三角开纸片,再将这两张三角形纸片摆放成如下右图的形式,使B、F、C、D在同一直线上。
①求证:AB⊥ED;②若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证实。

24、(本小题10分)心理学家发现学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系:y=-0.1x2 2.6x 43(0≤x≤30),y越大,表示接受能力越强。
①x在什么范围内学生的接受能力逐步增加?x在什么范围内,学生的接受能力逐渐降低?
②第10分钟时,学生的接受能力是多少?
③第几分钟时,学生的接受能力最强?最强时y值是多少?

25、(本小题12分)如图,有长为24米的篱笆,一面利用墙(墙的最在可用长度为10米),围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S米2。
①求S与x的函数关系式;②假如围成面积为45米2的花圃,AB的长是多少米?③能围成面积比45米2更大的花圃吗?假如能,请求出最大面积,并说明围法,假如不能,请说明理由。
26、(本题12分)(请仔细阅读题目后按要求解答)
某校301班数学老师布置在黑板上一个习题被当天值日生不慎擦掉了一部分(下面题中“……”即是被擦掉部分)习题原文如下:
①求证:此二次函数图像的对称轴为直线x=2;②求证:此函数图像顶点及x轴两交点能围成三角形的面积。
根据上述信息要求:
(1)求出b、c的值;
(2)将原题中的“……”处部分叙述在下面横线上:___________________________
(3)完成原题中的②。
27、(施展才华,强者必胜,祝你成功,本题为自选题,满分10分,分数可以加到前面,但试卷总分不超过120分)
探究一:(1)已知一直角三角形的二直角边之和为10,则当二直角边分别为________和________时,直角三角形的面积最大。此时的直角三角形为________(填外形)。
探究二:(2)已知一矩形的二边之和为10,则当这矩形的二边分别________和________时,矩形的面积最大。此时的矩形为________(填外形)。
探究三:利用探究一,探究二来解决下题:
已知正数a、b、c满足  则ab的最大值为多少?
则ab的最大值为多少?
参考答案:
一、1、5.3×10-4;2、AB=CD(等);3、22或23;4、19;5、(1,7);6、5;7、-2;
8、假如两个三角形是全等三角形,那么它们的对应边相等、对应角相等;9、4;10、1。
二、DBADA、CDBAC
三、21.(1)在△CAB和△DBA中,∵AC=BD,∠CAB=∠DBA,AB=BA
∴△CAB≌△DBA(SAS) ∴AD=BC(4分)
(2)∵△CAB≌△DBA ∴S△CAB=S△DBA ∴S△AOC=S△BOD 。(4分)
22.(1)m>5/4 (3分) (2)答案不唯一。(2分)
23.证实:由题意得:∠A ∠B=90º,∠A=∠D ∴∠D ∠B=90º ∴AB⊥DE(5分)
若PB=BC,由有Rt△ABC≌Rt△DBP,
∵∠B=∠B,∠A=∠D,DP=BC ∴Rt△ABC≌Rt△DBP(5分)
说明:图中和此条件有关的全等三角形还有如下几对:Rt△APN≌Rt△DCN,Rt△DEF≌Rt△DBP,Rt△EPM≌Rt△BFM,从中任选一对给证实,只要正确都得满分。
24.(1)当0≤x≤13时,学生的接受能力逐步增加。(2分)
(2)当13≤x≤30时,学生的接受能力逐步减少。(2分)
(3)当x=10时,y=59。(2分)
(4)∵y=-0.1(x-13)2 59.9, ∴当x=13时,y的最大值=59.9。(4分)
25.(1)设宽为xm,则BC=(24-3x)m (1分)
S=x·(24-3x)=-3x2 24x (2分)
(2)-3x2 24x=45,解方程得:x1=5,x2=3。(2分)
∵0<24-3x≤10,∴14/3≤x<8(1分)
∴x2=3不符合题意,舍去。∴x=5,即宽AB为5米。(1分)
(3)能。S=x·(24-3x)=-3x2 24x=-3(x-4)2 48,(2分)
又∵14/3≤x<8,∴当x=14/3时,S有最大值,
S的最大值=48-3×(14/3-4)2=140/3。(2分)
花圃的长为24-3×14/3=10,宽为14/3时,S的最大值为140/3。(1分)
26、(1)∵x=-b/2=2,∴b=-4(2分)
又∵y=x2-4x c经过A(-4,0),∴0=16 16 c,c=-32(2分)
(2)B(0,-32),且b<0(等)(4分)
(3)∵y=x2-4x-32经过A(-4,0),B(8,0)(1分)
y=(x-2)2-36,故它的顶点D为(2,-36)(1分)
△ACD的面积=AC×h×1/2=216(2分)
27、(1)分别为5和5,等腰直角三角形(2分)
(2)分别为5和5,正方形(2分)
(3)ab的最大值150-100 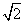 (6分)
(6分)
|