| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
根据上述计分规则和你制定的计分方案,确定两人谁在这次比赛中获胜.
 20. (本小题满分7分) 20. (本小题满分7分)
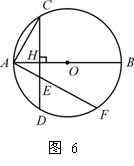
如图6,已知AB为⊙O的直径,弦CD⊥AB,垂足为H. (1) 求证:AH (2) 若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE (3) 若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判定AP 21. (本小题满分8分) 已知某项工程由甲、乙两队合做12天可以完成,共需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的2倍少10天,且甲队天天的工程费用比乙队多150元. (1) 甲、乙两队单独完成这项工程分别需要多少天? (2) 若工程治理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由. 22. (本小题满分8分)
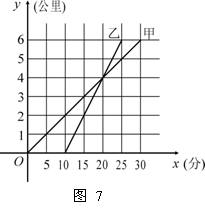 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题: 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图7. 根据图象解决下列问题:
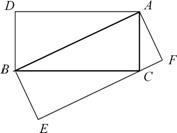
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间? (2) 分别求出甲、乙两人的行驶速度; (3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面. 23. (本小题满分9分) 阅读以下短文,然后解决下列问题: 假如一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”. 如图8①所示,矩形ABEF即为△ABC的“友好矩形”. 显然,当△ABC是钝角三角形时,其“友好矩形”只有一个 . (1) 仿照以上叙述,说明什么是一个三角形的“友好平行四边形”; (2) 如图8②,若△ABC为直角三角形,且∠C=90°,在图8②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小; (3) 若△ABC是锐角三角形,且BC>AC>AB,在图8③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证实.
24. (本小题满分9分) 如图9,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0). (1) 求点B的坐标; (2) 若二次函数y=ax2 bx c的图象经过A、B、O三点,求此二次函数的解析式; (3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.
资阳市2005年初中课改毕业年级学业考试暨高中阶段学校招生考试 数学试题参考答案及评分意见 说 明: 1. 解答题中各步骤所标记分数为考生解答到这一步的累计分数; 2. 给分和扣分都以1分为基本单位; 3. 参考答案都只给出一种解法,若考生的解答与参考答案不同,请根据解答情况参考评分意见给分 . 一、选择题:每小题4分,共10个小题,满分40分. 1-5. DABDC;6-10. CABCB. 二、填空题:每小题3分,共6个小题,满分18分. 11. (13题填为 三、解答题:共8个小题,满分62分 . 17.(1) a b c= b c d= (按考生的选择,得出正确结果都给分.正确写出所选a,b,c,d的值各1分,得出最后结果1分) (2)原式= =x2-y2 ···················································································· 7分 18.连结MN、PC、 CQ. ······································································· 1分 ∵点P是A点关于点M的对称点,∴ M是AP的中点, ························ 2分 又 M是BC的中点,∴ MN是△APC的中位线, ∴ CP∥MN .···························································································· 4分 同理可证,CQ∥MN . ············································································· 5分 从而,CP与CQ都经过点C且都平行于AB, ∴ P、C、Q三点在同一直线上. ····························································· 7分 (也可连结AQ、CQ、BP、CP,由ABCQ、ABPC为平行四边形证实,或根据全等三角形的性质证实) 19.(1)计分方案如下表:
| n(次)
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| M(分)
| 8
| 7
| 6
| 5
| 4
| 3
| 2
| 1 |
············································································································· 4分
(用公式或语言表述正确,同样给分.)
(2) 根据以上方案计算得6局比赛,甲共得24分,乙共得分23分,········· 6分
所以甲在这次比赛中获胜 . ····································································· 7分
20.(1) 连结CB,∵AB是⊙O的直径,∴∠ACB=90°. ························· 1分
而∠CAH=∠BAC,∴△CAH∽△BAC . ················································· 2分
∴ ![]()
![]()
(2) 连结FB,易证△AHE∽△AFB, ······················································ 4分
∴ AE ![]()
![]()
∴ AE ![]()
(也可连结CF,证△AEC∽△ACF)
(3) 结论AP ![]()
21.(1) 设甲队单独完成需x天,则乙队单独完成需要(2x-10)天.·············· 1分
根据题意有 ![]()
![]()
解得x1=3(舍去),x2=20.············································································ 4分
∴ 乙队单独完成需要 2x-10=30 (天).
答:甲、乙两队单独完成这项工程分别需要20天、30天. ······················· 5分
(没有答的形式,但说明结论者,不扣分)
(2) 设甲队天天的费用为y元,则由题意有
12y 12(y-150)=138000,解得y=650 . ····················································· 7分
∴ 选甲队时需工程费用650×20=13000,选乙队时需工程费用500×30=15000.
∵ 13000 <15000,
∴ 从节约资金的角度考虑,应该选择甲工程队.······································· 8分
22.(1) 甲先出发;先出发10分钟;乙先到达终点;先到5分钟. ········· 2分
(2) 甲的速度为每分钟0.2公里, ···························································· 3分
乙的速度为每分钟0.4公里 . ··································································· 4分
(3) 在甲出发后10分钟到25分钟这段时间内,两人都行驶在途中. ········ 5分
设甲行驶的时间为x分钟(10<x<25),则根据题意可得:
甲在乙的前面:0.2x>0.4(x-10) ; ··························································· 6分
甲与乙相遇:0.2x=0.4(x-10) ;································································ 7分
甲在乙后面:0.2x<0.4(x-10) .··································································· 8分
(设甲行驶的时间x时,没有限定范围的,不扣分. 也可设乙行驶的时间列出相应的方程或不等式 .)
 23. (1) 假如一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”. 1分
23. (1) 假如一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”. 1分
(2) 此时共有2个友好矩形,如图的BCAD、ABEF.
··········································································· 3分
易知,矩形BCAD、ABEF的面积都等于△ABC面积的2倍,∴ △ABC的“友好矩形”的面积相等. 4分
(3) 此时共有3个友好矩形,如图的BCDE、CAFG及ABHK,其中的矩形ABHK的周长最小 . 5分
证实如下:
易知,这三个矩形的面积相等,令其为S. 设矩形BCDE、CAFG及ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则
 L1=
L1= ![]()
![]()
![]()
∴ L1- L2=( ![]()
![]()
![]()
而 ab>S,a>b,
∴ L1- L2>0,即L1> L2 .······································ 8分
同理可得,L2> L3 .
∴ L3最小,即矩形ABHK的周长最小.······················································ 9分
24.(1) 在Rt△OAB中,∵∠AOB=30°,∴ OB= ![]()
![]()
![]()
![]()
(2) 将A(2,0)、B( ![]()
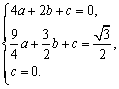
解方程组,有 a= ![]()
![]()
∴ 所求二次函数解析式是 y= ![]()
![]()
(3) 设存在点C(x , ![]()
![]()
![]()
∵△OAB面积为定值,
∴只要△OBC面积最大,四边形ABCO面积就最大. ······························· 5分
过点C作x轴的垂线CE,垂足为E,交OB于点F,则
S△OBC= S△OCF S△BCF= ![]()
![]()
················································································································ 6分
而 |CF|=yC-yF= ![]()
∴ S△OBC= ![]()
∴ 当x= ![]()
![]()
此时,点C坐标为( ![]()
![]()
| |