数 学（海门卷）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．共130分．考试时间120分钟．考试结束，将本试卷和答题卡一并交回．
第Ⅰ卷（选择题 共28分）
注重事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、考试号、科目名称用2B铅笔涂写在答题卡上．
2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案．不能答在试卷上．
一、选择题（本题共12小题；第1～8题每小题2分，第9～12题每小题3分，共28分）
下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的．
1． －2的倒数是
A．－2 B．－ 
2． 计算 
A． 
3． 下列角度中，是多边形内角和的只有
A．270° B．560° C．630° D．1800°
|
（第5题） |
4. 下列事件中，是确定事件的是
A．明年元旦海门会下雨 B．成人会骑摩托车
C．地球总是绕着太阳转 D．去北京要乘火车
5． “圆柱与球的组合体”如右图所示，则它的三视图是
|
俯视图 |
|
主视图 |
|
左视图 |
|
俯视图 |
|
主视图 |
|
左视图 |
|
俯视图 |
|
主视图 |
|
左视图 |
|
俯视图 |
|
主视图 |
|
左视图 |
|
. |
|
. |
 |
A． B． C． D．
|
° |
|
． |
|
0 |
|
2 |
|
－1 |
|
0 |
|
° |
|
2 |
|
－1 |
|
． |
|
． |
|
0 |
|
2 |
|
－1 |
|
． |
|
0 |
|
° |
|
° |
|
2 |
|
－1 |
6． 不等式组 
|
A |
|
D |
|
B |
|
C |
|
E |
|
（第7题） |
A． B． C． D．
7． 如图，在△ABC中，BC = 8 cm，AB的垂直平分线交AB
于点Ｄ，交边AC于点E，△BCE的周长等于18 cm，则
AC的长等于
A．6 cm B．8 cm
C．10 cm D．12 cm
8． 已知△ABC的三边长分别为6 cm，7.5 cm，9 cm，△DEF
的一边长为4 cm，当△DEF的另两边长是下列哪一组时，这两个三角形相似
A．2 cm，3 cm B．4 cm，5 cm
C．5 cm，6 cm D．6 cm，7 cm
|
（第9题） |
|
A |
|
D |
|
C |
|
B |
9． 如图，已知AD是△ABC的外接圆的直径，AD =13 cm， 
A．5 cm B．6 cm
C．10 cm D．12 cm
10．某学习小组在讨论 “变化的鱼”时，知道大鱼与小鱼是位似图形
|
y |
|
x |
|
O |
|
（第10题） |
|
2 |
|
－1 |
|
1 |
（如图所示）．
|
y |
|
x |
|
1 |
|
O |
|
（第11题） |
|
－1 |
|
O －3 |
 |
则小鱼上的点（a，b）对应大鱼上的点
A．（－2a，－2b） B．（－a，－2b）
C．（－2b，－2a） D．（－2a，－b）
11．已知抛物线 
取值范围是
A．－1＜x＜4 B．－1＜x＜3
C．x＜－1或 x＞4 D．x＜－1或 x＞3
12．用3根火柴棒最多能拼出
A．4个直角 B．8个直角
|
|
座位号
| |
C．12个直角 D．16个直角
第Ⅱ卷（共102分）
注重事项：
用钢笔或圆珠笔将答案直接写在试题卷上．
题号
二
三
四
五
六
Ⅱ卷总分
结分人
核分人
26
27
28
得分
|
|
得分
| 评卷人
|
| |
二、填空题（本题共6小题；每小题3分，共18分）
请把最后结果填在题中横线上．
13．把数103000用科学记数法表示，结果是 ．
14．若x∶y =1∶2，则 
|
P1 |
|
O |
|
x |
|
y |
|
A1 |
|
A2 |
|
P2 |
|
（第18题） |
15．若两圆外切，圆心距为8cm，一个圆的半径为3 cm，则另一个圆的半径为 cm．
16．计算 
17．已知圆锥的母线与高的夹角为30°，母线长为4cm，则
它的侧面积为 cm2（结果保留 
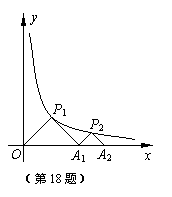
18．如图，△P1O A1、△P2 A1 A2是等腰直角三角形，点P1、
P2在函数 
在x轴上，则点A2的坐标是 ．
|
三、解答题（本题共2小题；共17分）
19．（本小题10分）
（1）计算 
20．（本小题7分）
解方程 
|
四、解答题（本题共3小题；共22分）
21．（本小题7分）
|
C |
|
O |
|
D |
|
E |
|
F |
|
（第21题） |
如图，一条公路的转弯处是一段圆弧 
22．（本小题7分）
海门市三星镇的叠石桥国际家纺城是全国最大的家纺专业市场，年销售额突破百亿元．
2005年5月20日，该家纺城的羽绒被和羊毛被这两种产品的销售价如下表：
品 名
规格（米）
销售价（元/条）
羽绒被
2×2.3
415
羊毛被
2×2.3
150
现购买这两种产品共80条，付款总额不超过2万元．问最多可购买羽绒被多少条?
23．（本小题8分）
|
n=3 |
|
n=4 |
|
n=5 |
|
（第23题） |
|
…… |
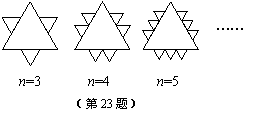已知一个面积为S的等边三角形，现将其各边n（n为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．
（1）当n = 5时，共向外作出了 个小等边
三角形，每个小等边三角形的面积为 ；
（2）当n = k时，共向外作出了 个
小等边三角形，这些小等边三角形的面积和
为 （用含k的式子表示）．
|
|
（第24题 图1） |
五、解答题（本题共2小题；共16分）
24．（本小题8分）
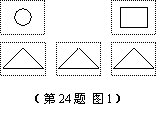
杨华与季红用5张同样规格的硬纸片做拼图游戏，正面如图1
所示，背面完全一样，将它们背面朝上搅匀后，同时抽出两张．
规则如下：
当两张硬纸片上的图形可拼成电灯或小人时，杨华得1分；
当两张硬纸片上的图形可拼成房子或小山时，季红得1分（如图2）．
问题：游戏规则对双方公平吗？请说明理由；若你认为不公平，如何修改游戏规则才能使游
|
房子 |
|
电灯 |
|
小山 |
|
小人 |
|
（第24题 图2） |
戏对双方公平？
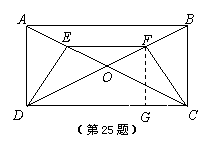
25．（本小题8分）
如图，矩形ABCD的对角线AC、BD相交于点O，E、F分别是OA、OB的中点．
（1）求证：△ADE≌△BCF；
（2）若AD = 4cm，
|
（第25题） |
A |
B |
C |
|
D |
E |
O |
F |
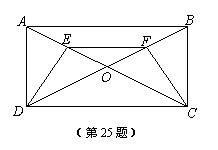AB = 8cm，求CF的长．
六、解答题（本题共3小题；共29分）
|
26．（本小题9分）
|
|
（1）这五个城市2004年商品房销售均价的中位数、极差分别是多少？
（2）若2002年A城市的商品房销售均价为1600元/平方米，试估计A城市从2002年到
2004年商品房销售均价的年平均增长率约是多少（要求误差小于1%）？
|
|
得分
| 评卷人
|
| |
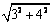
27．（本小题9分）
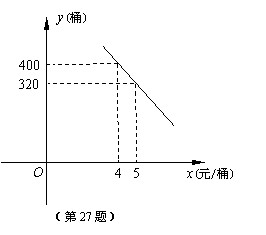
某校八年级（1）班共有学生50人，据统计原来每人每年用于购买饮料的平均支出是a元．经测算和市场调查，若该班学生集体改饮某品牌的桶装纯净水，则年总费用由两部分组成，一部分是购买纯净水的费用，另一部分是其它费用780元，其中，纯净水的销售价x(元/桶)与年购买总量y (桶)之间满足如图所示关系．
（1）求y与x的函数关系式；
（2）若该班每年需要纯净水380桶，且a 为120时，请你根据提供的信息分析一下：该班学生集体改饮桶装纯净水与个人买饮料，哪一种花钱更少？
|
y(桶) |
|
x(元/桶) |
|
O |
|
4 |
|
5 |
|
400 |
|
320 |
|
（第27题） |
（3）当a至少为多少时, 该班学生集体改饮桶装纯净水一定合算？从计算结果看，你有何感想（不超过30字）？
|
|
得分
| 评卷人
|
| |
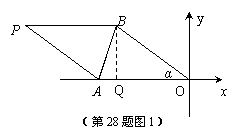
28．（本小题11分）
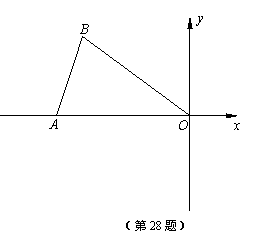
如图，在平面直角坐标系中，已知A（－10，0），B（－8，6），O为坐标原点，△OAB沿AB翻折得到△PAB．将四边形OAPB先向下平移3个单位长度，再向右平移m（m＞0）个单位长度，得到四边形O1A1P1B1．设四边形O1A1P1B1与四边形OAPB重叠部分图形的周长为l．
（1）求A1、P1两点的坐标（用含m的式子表示）；
（2）求周长l与m之间的函数关系式，并写出m的取值范围．
|
OS |
|
y |
|
B S |
|
x |
|
（第28题） |
|
A |
 |
2005年南通市中等学校招生考试
数学（海门卷）参考答案与评分标准
一、选择题(本题共12小题；第1～8题每小题2分，第9～12题每小题3分，共28分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
D
C
A
B
C
C
D
A
B
C
二、填空题(本题共6小题；每小题3分，共18分)
13．1.03×105 14． 
三、解答题（本题共2小题；共17分）
19．（本小题10分）
解：（1）原式＝ 
＝－6＋8－3
＝－1． ………………………………………………5分
（2）原式＝ 
＝ 
＝－6 ． ………………………………………………5分
20．（本小题7分）
解：去分母，得x―3－(4－x)＝－1． ……………………………………………………2分
去括号、整理，得2 x＝6．
解得 x＝3． …………………………………………………5分
检验：将x＝3代入原方程，得
左边＝－1＝右边,
所以，x＝3是原方程的解． …………………………………………………… 7分
四、解答题（本题共3小题；共22分）
21．（本小题7分）
|
C |
|
O |
|
D |
|
E |
|
F |
|
（第21题） |
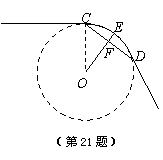
则OF＝OE－EF＝R－100．
∵OE⊥CD，
∴CF＝ 
根据勾股定理，得
OC2＝CF2＋OF2，
即 R2＝3002＋（R－100）2． ……………………5分
解之，得 R＝500．
所以这段弯路的半径为500米． ……………………7分
22．（本小题7分）
解：设购买羽绒被x条，则购买羊毛被(80－x)条，
根据题意，得
415x＋150(80－x)≤20000． ………………………………………………3分
整理，得
265x≤8000．
解之，得 x≤ 
∵x为整数，∴x的最大整数值为30．
答：最多可购买羽绒被30条． ……………………………………………………7分
23．（本小题8分）
解：（1）9， 
（2）3（k－2）， 
五、解答题（本题共2小题；共16分）
24．（本小题8分）
解：（1）这个游戏对双方不公平． ………………………………………………1分
∵ 
∴杨华平均每次得分为 
季红平均每次得分为 
∵ 
（2）改为：当拼成的图形是小人时杨华得3分，其余规则不变，
就能使游戏对双方公平．（答案不惟一，其他规则可参照给分） ………………8分
25．（本小题8分）
（1）证实：∵四边形ABCD为矩形，
∴AD＝BC，OA＝OC，OB＝OD，AC＝BD， AD∥BC，
∴OA＝OB＝OC，∠DAE＝∠OCB，∴∠OCB＝∠OBC，
∴∠DAE＝∠CBF． …………………………………………2分
又∵AE＝ 
∴△ADE≌△BCF． …………………………………………………4分
（2）解：过点F作FG⊥CD于点G，则∠DGF＝90º，
A |
B |
|
（第25题） |
C |
|
D |
E |
O |
F |
G |
 |
∵∠DCB＝90º，
∴∠DGF＝∠DCB，
又∵∠FDG＝∠BDC，
∴△DFG∽△DBC，
∴ 
由（1）可知DF＝3FB，得 
∴ 
∴GC＝DC－DG＝8－6＝2． ……………7分
在Rt△FGC中， 
（说明：其他解法可参照给分，如延长CF交AB于点H，利用△DFC∽△BFH计算．）
六、解答题（本题共3小题；共29分）
26．（本小题9分）
解：（1）中位数是2534（元/平方米）； ……………………………………………2分
极差是3515－2056＝1459（元/平方米）． ………………………………4分
（2）设A城市2002年到2004年的年平均增长率为x，由题意，得
1600(1＋x)2＝2119． ………………………………………………………7分
(1 x)2＝1.324375，
∵x＞0，∴1 x＞0，
当x＝0.15时， (1 x)2＝1.152＝1.3225＜1.324375，
当x＝0.16时， (1 x)2＝1.162＝1.3456＞1.324375，
可知 1.15＜1＋x＜1.16，∴0.15＜x＜0.16．
答：平均增长率约为15%（或16%等，答案不惟一）． ………………………9分
27．（本小题9分）
解：（1）设 
∴ 
∴y与x的函数关系式为 
（2）该班学生买饮料每年总费用为50×120＝6000（元），
当y＝380时， 
该班学生集体饮用桶装纯净水的每年总费用为380×4.25 780＝2395(元),
显然，从经济上看饮用桶装纯净水花钱少． …………………………5分
（3）设该班每年购买纯净水的费用为W元，则
W ＝xy＝x（－80x 720）＝ 
∴当 x＝ 
要使饮用桶装纯净水对学生一定合算，
则 50a≥W最大值 780，即 50a≥1620 780，
解之，得 a≥48．
所以a至少为48元时班级饮用桶装纯净水对学生一定合算， ………8分
由此看出，饮用桶装纯净水不仅能省钱，而且能养成勤俭节约的好习惯． ……9分
28．（本小题11分）
解：（1）过点B作BQ⊥OA于点Q．（如图1）
|
O －3 |
|
y |
|
B |
|
x |
|
A |
|
P |
|
Q |
|
α |
|
（第28题图1） |
∵ 点A坐标是（－10，0），
∴点A1坐标为（－10＋m，－3），OA＝10．
…………………………………………1分
又∵ 点B坐标是（－8，6），
∴BQ＝6，OQ＝8．
在Rt△OQB中，
∴OA＝OB＝10， 
由翻折的性质可知，PA＝OA＝10，PB＝OB＝10， ∴四边形OAPB是菱形，
∴PB∥AO，∴P点坐标为（－18，6）， ……………………………4分
∴P1点坐标为（－18＋m，3）． …………………………………………5分
（2）①当0＜m≤4时，（如图2）, 过点B1作B1Q1⊥x轴于点Q1，则B1 Q1＝6-3＝3，
设O1B1 交x轴于点F，∵O1B1∥BO，∴∠α＝∠β，
|
x |
|
O |
|
y |
|
B |
|
A |
|
P1 |
|
A1 |
|
O1 |
|
B1 |
|
Q1 |
|
F |
|
α |
|
Q |
|
β |
|
（第28题图2） |
|
P |
在Rt△FQ1B1中， 
∴ 
∴B1F＝
∵AQ＝OA－OQ＝10－8＝2，
∴AF＝AQ QQ1 Q1F＝2 m 4＝6 m，
∴周长l＝2（B1F＋AF）
＝2（5＋6＋m）
＝2 m＋22； ……………8分
|
x |
|
O |
|
B |
|
A |
|
P1 |
|
A1 |
|
O1 |
|
B1 |
|
（第28题图3） |
|
P |
|
S |
|
H |
|
F |
|
y |
 |
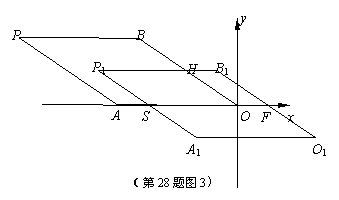②当4＜m＜14时，（如图3）
设P1A1交x轴于点S，P1B1交OB
于点H，
由平移性质，得 OH＝B1F＝5，
此时AS＝m－4，
∴OS＝OA－AS
＝10－（m－4）＝14－m，
∴周长l＝2（OH＋OS）
＝2（5＋14－m）
＝－2 m＋38． ……………11分
