| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
(A)2种 (B)3种 (C)4种 (D)5种 28.如图,外切于P点的⊙⊙ (A)
29.某商店把一商品按标价的九折出售(即优惠10%),仍可获利20%,若该商品的标价为每件28元,则该商品的进价为( ). (A)21元 (B)19.8元(C)22.4元 (D)25.2元 30.抛物线 ③ (A)①② (B)②③ (C)②④ (D)③④ 31.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图,若返回时上、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )。 (A)37.2分钟 (B)48分钟 (C)30分钟 (D)33分钟 32.已知:如图, (A)①② (B)③④ (C)①②③ (D)①②④ 四、填空题(共4小题,每小题2分,共8分) 33.(本题共有A、B两小题,请你只选择一题作答) A.请你写出一个能分解的二次四项式并把它分解 。 B.用计算器计算: 34.在同一平面上,1条直线把一个平面分成
36.如图,
五、证实与解答题(本大题共3小题,共22分) 37.(本题6分)武汉市教育局在中学开展的“创新素质实践行”中,进行了小论文的评选。各校交论文的时间为5月1日至30日,评委会把各校交的论文的件数按5天一组分组统计,绘制了频率分布直方图,已知从左至右各长方形的高的比为2:3:4:6:4:1,第二组的频数为18。请回答下列问题: (1)本次活动共有多少篇论文参加评选? (2)哪组上交的论文数量最多?有多少篇? (3)经过评选,第四组和第六组分别有20篇、4篇论文获奖,问这两组哪组获奖率较高? 38.(本题8分)如图,已知:⊙
(1)请你判定 (2)将“⊙ 39.(本题8分)2004年8月中旬,我市受14号台风“云娜”的影响后,部分街道路面积水比较严重。为了改善这一状况,市政公司决定将一总长为1200m的排水工程承包给甲、乙两工程队来施工。若甲、乙两队合做需12天完成此项工程;若甲队先做了8天后,剩下的由乙队单独做还需18天才能完工。问甲、乙两队单独完成此项工程各需多少天?又已知甲队每施工一天需要费用2万元,乙队每施工一天需要费用1万元,要使完成该工程所需费用不超过35万元,则乙工程队至少要施工多少天? 六、综合题(本题10分) 40.已知抛物线 (1)求抛物线的解析式; (2)是否存在与抛物线只有一个公共点C的直线。假如存在,求符合条件的直线的表达式;假如不存在,请说明理由。 七、综合题(本题14分) 41.已知:如图,直线 (1)求证: (2)求证:EF是⊙ (3)
参考答案 A卷共60分
| 题号
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 答案
| B
| A
| A
| A
| A
| A
| A
| B
| A
| A | ||||||||||||||||||||||||||||||
二、选择题(每小题4分,共40分)
题号
11
12
13
14
15
16
17
18
19
20
答案
C
D
A
B
A
C
C
D
A
D
B卷(共90分)
三、选择题(共12小题,每小题3分,共36分)
题号
21
22
23
24
25
26
27
28
29
30
31
32
答案
C
B
B
A
A
C
D
A
A
B
A
D
四、填空题(共4小题,每小题2分,共8分)
33.A如 ![]() B 2.35
B 2.35
34.37 35.AB=AC或BD=DC 36. ![]()
五、证实与解答题(本大题共3小题,共22分)
37.(本题6分)答:(1)本次活动共有120篇论文参评;
 (2)第四组上交的论文数量最多,有36篇;
(2)第四组上交的论文数量最多,有36篇;
(3)第六组获奖率最高。
38.(本题8分)(1)∠BPC=∠CPD成立。
(2)解:(1)中的结论仍然成立。
过点P作两圆的公切线PM,
则∠MPB=∠A,∠MPC=∠BCP。
∴∠BPC=∠MPC-∠MPB=∠BCP-∠A=∠CPA。
∴∠BPC=∠CPD
39.解:设甲、乙两队单独完成此项工程分别需要x天,y天。
依题意得 
解之得 ![]()
经检验知它们适合方程组和题意。
则甲队天天施工1200÷20=60m,乙队天天施工1200÷30=40m.
设甲、乙两队实际完成此项工程分别需要a天,b天.
依题意得 ![]()
解之得b≥35.
答:甲、乙两队单独完成此项工程分别需要20天,30天;要使完成该工程所需费用不超过35万元,则乙工程队至少要施工15天。
六、综合题(本题10分)
40.解:(1)由条件知AO=| ![]() |=-
|=- ![]() ,OB=|
,OB=| ![]() |=
|= ![]() ,OC=3(m 1).
,OC=3(m 1).
∵ ![]() ,
,
![]() ,
,
![]()
![]()
得: ![]() .
.
∵ ![]() <
< ![]() ,|
,| ![]() |>|
|>| ![]() |,
|,
∴ ![]() <
< ![]() =m-2<0,∴m=1.
=m-2<0,∴m=1.
∴函数的解析式为 ![]()
(2)存在与抛物线只有一个公共点C的直线.
C点的坐标为(0,6).
①当直线过C(0,6)且与x轴垂直时,直线也抛物线只有一个公共点,
∴直线 ![]() 。
。
②过C点的直线 ![]() ,与抛物线
,与抛物线 ![]() 只有一个公共点C,
只有一个公共点C,
即  只有一个实数解。
只有一个实数解。
∴ ![]() ,
,
![]() ,∴
,∴ ![]() ,∴
,∴ ![]() 。
。
∴ ![]() 。
。
∴符合条件的直线的表达式为 ![]() 或
或 ![]() 。
。
七、综合题(本题14分)
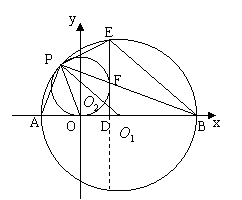 41.证实:(1)连结
41.证实:(1)连结 ![]() 。
。
∵ ![]() 。
。
∴ ![]() ,
,
![]() ,
,
∴ ![]() .
.
∴ ![]() ,
,
得 ![]() ,∴
,∴ ![]() 。
。
又AB为直径,∴ ![]() ,
,
∴ ![]() 。
。
(2)延长ED交⊙ ![]() 于点H,连结PE。
于点H,连结PE。
BO为切线,∴ ![]() 。
。
又∵BE=BO,∴ ![]() 。
。
而 ![]() ,∴
,∴ ![]() ∽
∽ ![]() ,
,
∴ ![]() , ∴BE=BH,
, ∴BE=BH,
有 ![]() 。
。
又由(1)知 ![]() ,∴
,∴ ![]() ,
,
∴EF为⊙ ![]() 的切线。
的切线。
(3)MN的长度不变。
过N作⊙ ![]() 的直径NK,连结MK。
的直径NK,连结MK。
则 ![]() ,
,
且 ![]() ,又NK=
,又NK= ![]() ,
,
∴ ![]() ≌
≌ ![]() ,∴MN=ED。
,∴MN=ED。
而 ![]() ,
, ![]() ,∴
,∴ ![]()
![]() =5,
=5,
∴ ![]() 。
。
AB=16,且OD= ![]() ,∴AD=7,BD=9。
,∴AD=7,BD=9。
![]() ,∴
,∴ ![]()
![]() 。
。
故MN的长度不会发生变化,其长度为 ![]() 。
。
| |