| |
|
[组图]湖北省黄冈中学初三中考模拟考试
|
| 查询数中考复习的详细结果
|
|
初三中考模拟考试
数 学 试 题(2004年中考数学模拟试卷(11))
(满分:120分,考试时间:120分)
姓名 学号 得分
一、填空题(每小题3分,共18分)
1.– 0.2的倒数是 ,在数轴上表示有理数a的点到原点的距离为1,则a = ,若一个实数的平方根为b – 3和3b 7,则b = ;
2.计算: EQ \F(1,3) x 2y·(– 6xy 2)= ,函数y = EQ \F((x - 1) 0 2,\R(,3 x)) 中,自变量x的取值范围是 ,
化简:– EQ \R(,- a 3) = ;
3.已知a、b是方程t 2 – t – 4 = 0的两根,那么因式分解(a b)x 2 y 2 – 2xy ab = ;
4.当x = cos60°时, EQ \F(12 - 3x,x x - 2) ÷ (x - 2 - \F(3x,x 2)) 的值为 ;
 5.把一个半径为8cm的圆片,剪去一个圆心角为90°的扇形后,剩下的部分做成一个圆锥的侧面,那么这个圆锥的高为 ; 5.把一个半径为8cm的圆片,剪去一个圆心角为90°的扇形后,剩下的部分做成一个圆锥的侧面,那么这个圆锥的高为 ;
6.如图,⊙O半径为1,P为⊙O外的一点,PA切⊙O于点A,PA = 1,
若AB是⊙O的弦,切AB = EQ \R(,2) ,则PB的长为 ;
二、选择题(每小题3分,共15分)
7.下列二次根式中① EQ \R(,\F( x ,2)) ; EQ ② EQ \R(,8) ;③ EQ \R(,x 2) ;④ EQ \R(,x 2 1) 属于最简二次根式的有 ( )
A.1个 B.2个 C.3个 D.4个
8.如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是 ( )
A.AB = CD B.AC = BD
C.当AC⊥BD时,它是菱形 D.当∠ABC = 90°时,它是矩形
9.在△ABC中,∠C = 90°,AC = 2 EQ \R(,5) ,∠A的平分线交BC于D,且AD = EQ \F(4,3) \R(,15) ,则tan∠BAC的值等于 ( )

 A. EQ \F( 1 ,3) B. EQ \F( \R(,3) ,3) C. EQ \R(,3) D. EQ \F(8,3) \R(,15) A. EQ \F( 1 ,3) B. EQ \F( \R(,3) ,3) C. EQ \R(,3) D. EQ \F(8,3) \R(,15)
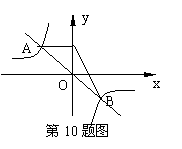
10.如图,函数y = – kx(k≠0)与y = EQ \F(- 4,x) 的图象交于A、B两点,过点A作AC⊥y轴,垂足为C,则△BOC的面积为 ( )
A.1 B.4 C.3 D.2
11.某商场将一种商品A按标价的9折出售,依然可获利10%,若商品A的标价为33元,
那么该商品的进货价为( )
A.31元 B.30.2元 C.29.7元 D.27元
三、解答题
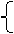
x 2 – 2x 3y – 5 = 0
x – y 1 = 0
13.(6分)已知:如图,在梯形ABCD中,AB = CD,AD // BC,点E在AD上,且EB = EC。
 求证:AE = DE 求证:AE = DE
14.(5分)某居民小区开展节约用水活动成效显著,据对该小区200户家庭用水情况统计分析,3月份比2月份节约用水情况如下表所示: |
节水量(立方米) |
1 |
1.5 |
2 | |
户 数 |
20 |
120 |
60 | |
(1)填空:节水量的众数是 ;
(2)求3月份平均每户节约用水多少立方米?
四.多项选择题(每小题4分,共8分)
15.已知抛物线y = ax 2 bx c(a<0=经过(– 1,0)点,且满足4a 2b c>0,以下结论中,正确的是 ( )
A.abc>0 B.9a 3b c>0 C.– a b c>0 D.a c>0
 16.如图,AB是半圆O的直径,D为BC的中点,DE⊥AC于E,延长ED、AB交于点F,若DF = 5,BF = 2.5,则下列结论中正确的是( ) 16.如图,AB是半圆O的直径,D为BC的中点,DE⊥AC于E,延长ED、AB交于点F,若DF = 5,BF = 2.5,则下列结论中正确的是( )
A.EF是⊙O的切线 B.圆O的半径为 EQ \F(15,4)
C.AE = 6 D.DF 2 = BF 2 AB·BF
五、解答题
17.(8分)黄冈某灯具店采购了一批某种型号的节能灯,共用去400元,在搬运的过程中不慎打坏了5站,该店把余下的灯每站加价4元全部售完,然后用所得的钱又采购了一批这种节能灯,且价与上次相同,但购买的数量比上次多了9站,求每站灯的进价是多少元?
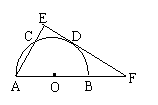
 18.(9分)如图,已知⊙O是△ABC的内切圆,切点分别为D、E、F,AB = AC,连结AD交⊙O于H,直线HF交BC的延长线于G。 18.(9分)如图,已知⊙O是△ABC的内切圆,切点分别为D、E、F,AB = AC,连结AD交⊙O于H,直线HF交BC的延长线于G。
(1)求证:AD经过O点; (2)CD = CG;
(3)若 EQ \F(AH,AF) = \F( 3 ,4) ,CG = 10,求HF的长;
19.(8分)阅读下列材料:三角形重心定理:
三角形的三条中线交于一点(该点叫三角形的重心),这点到顶点的距离等于它到对边中点距离的两倍。
已知:AD、BE和CF是△ABC的三条中线。
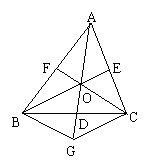 求证:AD、BE和CF相交于一点,这点到顶点的距离等于它到对边中点距离的两倍。 求证:AD、BE和CF相交于一点,这点到顶点的距离等于它到对边中点距离的两倍。
证实:如图,设中线BE、CF相交于O点,由三角形中位线定理知:
   AE = EC EF // BC AE = EC EF // BC
 AF = BF EF = EQ \F(1,2) BC AF = BF EF = EQ \F(1,2) BC
   EQ \F(OF,OC) = \F(OE,OB) = \F(EF,BC) OB = 2OE EQ \F(OF,OC) = \F(OE,OB) = \F(EF,BC) OB = 2OE
BC = 2 EF OC = 2OF
连结AO并延长交BC于D,过点C作CG // BE交AD的延长线于G,连结BG

      OE // CG CG = 2OE CG = BO OE // CG CG = 2OE CG = BO
AE = EC BO = 2OE CG // BO
故AD、BE、CF相交于点O,且BO = 2OE,AO = 2OD,CO = 2OF。
用三角形重心定理解答下列问题:
如图,Rt△ABC中,斜边BC = 6,AD、BE是中线,若AD⊥BE于G。
(1)填空:BG = GE,DG = AD,AD = BC;
 (2)求中线BE的长。 (2)求中线BE的长。
20.(9分)张某要在一个长为25cm,宽为18cm的矩形铁片上,剪去一个和三边都相切的⊙A后,在剩余部分的废料上再剪去一个最大的⊙B,因张某不会计算,请你帮他求出⊙B的直径。
21.(12分)某商店钢笔每支25元,该店为促销制定了两种优惠方法:① 买钢笔一支赠予笔记本一个;② 按购买总额的90 %付款。
(1) 某单位需要钢笔10支,笔记本x(x≥10)个,则每种优惠方法的实际付款数y(元)是x的函数,表达式分别为:
y1 = ;y 2 = ;
(2) 若该单位花495元购回了所需物品,问采用哪一种优惠方法比较花算?
(3) 若可以任选一种方法购买,也可以同时两种方法购买,还可以在一种优惠方法中只买一种物品,请你就购买10支钢笔和60个笔记本设计一种最省钱的购买方法。
22.(16分)已知抛物线y = EQ \F(1,3) x 2 bx c与x轴交于点A(– 3,0),与y轴交于点E(0,– 1)。
(1) 求此抛物线的解析式;
(2) 若Q(m,n)在此抛物线上,且– 3≤m≤3,求n的取值范围;
答: (本小题不必写解的过程,只需将答案直接写在横线上)
(3) 设点B是抛物线与x周的另一个交点,P是抛物线上异于点B的一个动点,连结BP交y轴于点N(点N在点E的上方),若△AOE与△BON相似,求点P的坐标。
(4) 设(1)中的抛物线的顶点为M,求以A、M、B为顶点的平行四边形的第四个顶点C的坐标。(直接写出点的坐标),其中是否有菱形,若有,写出哪一点的坐标是菱形的第四个顶点的坐标。
|
 16.如图,AB是半圆O的直径,D为BC的中点,DE⊥AC于E,延长ED、AB交于点F,若DF = 5,BF = 2.5,则下列结论中正确的是( )
16.如图,AB是半圆O的直径,D为BC的中点,DE⊥AC于E,延长ED、AB交于点F,若DF = 5,BF = 2.5,则下列结论中正确的是( )
 18.(9分)如图,已知⊙O是△ABC的内切圆,切点分别为D、E、F,AB = AC,连结AD交⊙O于H,直线HF交BC的延长线于G。
18.(9分)如图,已知⊙O是△ABC的内切圆,切点分别为D、E、F,AB = AC,连结AD交⊙O于H,直线HF交BC的延长线于G。
 求证:AD、BE和CF相交于一点,这点到顶点的距离等于它到对边中点距离的两倍。
求证:AD、BE和CF相交于一点,这点到顶点的距离等于它到对边中点距离的两倍。
 (2)求中线BE的长。
(2)求中线BE的长。