|
中考数学复习同步检测(27) 姓名
(圆的基本性质1)
一.填空题:
1.有长、宽分别为4 cm、3 cm的矩形ABCD,以A为圆心作圆,若B、C、D至少与一点且至少只有一点在圆内,则圆的半径R的取值范围是 ;
2.圆的一条弦与直径相交成  的角,且把直径分为1 cm和5 cm,那么这弦的弦心距为
的角,且把直径分为1 cm和5 cm,那么这弦的弦心距为
cm,弦长为 cm;
 3.⊙O的半径为2 cm,P为⊙O内一点,且PO = 1 cm,则⊙O过P点的弦中,最短的弦长为 cm,它所对的劣弧为 度; 3.⊙O的半径为2 cm,P为⊙O内一点,且PO = 1 cm,则⊙O过P点的弦中,最短的弦长为 cm,它所对的劣弧为 度;
4.内接于圆的非凡四边形是 ;
5.如图2,AB、AC为⊙O的两条弦,延长CA到D,使AD = AB;
假如∠ADB =  ,那么∠BOC = ;
,那么∠BOC = ;
6.一个半径是5cm的圆,它的一条弦长是6cm,则弦心距是 ;
7.已知,等边ΔABC内接于⊙O,AB=10cm,则⊙O的半径是 ;
8.一条弦把圆分成2:3两部分,那么这条弦所对的圆心角的度数是 ;
  9.已知圆O的弦AB经过弦CD的中点P,若AP=2cm,CD=8cm,则PB的长是 ; 9.已知圆O的弦AB经过弦CD的中点P,若AP=2cm,CD=8cm,则PB的长是 ;
10.如图(5),弧  的度数是
的度数是  ,则
,则  ;
;
11.如图(6),  ,则
,则  ;
;
 12.如图(7), 12.如图(7),  ,
,  ,则
,则 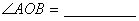 。
。
13.已知某圆的半径是  ,请写出它的其中一条弦的长度____________。
,请写出它的其中一条弦的长度____________。
 14.如图(8),弦 14.如图(8),弦  ,
,  的半径为
的半径为 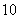 ,
,  ,
,  ,
,
 则 则  、
、 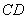 之间的距离是___________
之间的距离是___________  ;
;
15.如图(9), 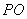 是直径所在的直线,且
是直径所在的直线,且 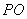
平分  ,
,  ,
,  ,则:
,则:
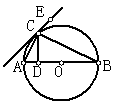 ① ①  ;②弧
;②弧  等于弧
等于弧 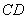 ;③
;③ 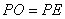 ;
;
④弧  等于弧
等于弧 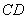 ;⑤
;⑤  ;其中结论正确的是________________(填序号) 。
;其中结论正确的是________________(填序号) 。
16.7、如图,AB为⊙O的直径,CE切⊙O于点C,CD⊥AB,D为垂足,
 AB=12cm,∠B=30°,则∠ECB= 度,CD= cm; AB=12cm,∠B=30°,则∠ECB= 度,CD= cm;
 17.如图,DE是⊙O的直径,弦AB⊥DE,垂足为C , 17.如图,DE是⊙O的直径,弦AB⊥DE,垂足为C ,
若AB=6,CE=1,则CD= ,OC= ;
18.如图, 四边形ABCD内接于⊙O, M为AB
延长线上一点. 已知∠AOC=130°, 则∠MBC=_______度;
二.选择题:
18.三角形的外心是这个三角形的三条中位线组成的三角形的 ( )
A 外心 B 垂心 C 重心 D 以上答案都不对
 19.如图,以等腰三角形的腰为直径作圆,交底边于D,连结AD, 19.如图,以等腰三角形的腰为直径作圆,交底边于D,连结AD,
那么 ( )
A ∠1 ∠2 = 90  B ∠1
B ∠1  ∠2
∠2
C ∠1 =∠2 D ∠1  ∠2
∠2
20.下列命题中,真命题的个数为 ( )
①所有过圆心的直线都是圆的对称轴;②任意一条弦所在的直线都是圆的对称轴,③任意一条弦的垂直平分线都是圆的对称轴;④任意一条直径所在的直线都是圆的对称轴
 A 1个 B 2 个 C 3 个 D 4 个 ( ) A 1个 B 2 个 C 3 个 D 4 个 ( )
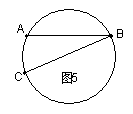
21.如图:B、C、D在⊙O上,∠BOD = 100  ,则∠BCD ( )
,则∠BCD ( )
 A 130 A 130  B 100
B 100  C 80
C 80  D 50
D 50 
 22.在⊙O中, AB = 2 AC,那么 ( ) 22.在⊙O中, AB = 2 AC,那么 ( )
A AB = AC B AB =2 AC C AB  2AC D AB
2AC D AB  2AC
2AC
23.⊙O的弦AB等于半径,那么弦AB所对的圆周角一定是 ( )
A 30  B 150
B 150  C 30
C 30  或150
或150  D 60
D 60 
 24.如图,在⊙O的内接四边形ABCD中,∠BOD = 120 24.如图,在⊙O的内接四边形ABCD中,∠BOD = 120  ,那么∠BCD是 ( )
,那么∠BCD是 ( )
A 120  B 100
B 100  C 80
C 80  D 60
D 60 
25.下列命题中真命题是 ( )
A 平分弦的直径垂直于弦 B. 圆的半径垂直于圆的切线
 C. 到圆心的距离大于半径的点在圆内 D. 等弧所对的圆心角相等 C. 到圆心的距离大于半径的点在圆内 D. 等弧所对的圆心角相等
26.如图10,AB是⊙O的直径,CD是⊙O弦,若AB=10cm,CD=8cm,
那么A、B两点到直线CD的距离之和为 ( )
A. 12cm B. 10cm C. 8cm D. 6cm
27.下面命题中,是真命题的有 ( )
①平分弦的直径垂直于弦;②假如两个三角形的周长之比为3∶  ,则其面积之比为3∶4;③圆的半径垂直于这个圆的切线;④等弧所对的圆心角相等;⑤过三点有且只有一个圆。
,则其面积之比为3∶4;③圆的半径垂直于这个圆的切线;④等弧所对的圆心角相等;⑤过三点有且只有一个圆。
 A 1个 B 2个 C 3个 D 4个 A 1个 B 2个 C 3个 D 4个
28.如图,⊙O的直径AB=10,E是OB上一点,弦CD过点E,
且BE=2,ED=2  ,则弦心距OF为 ( )
,则弦心距OF为 ( )
A 1 B  C
C  D
D 
三.解答题:
29.如图,AB是⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D。求证:AC平分∠DAB。

30.已知,如图,⊿ABC内接于⊙O,D是AC 的中点,BD交AC于点E,求证: 

31.如图6,已知△ABC是⊙O的内接三角形,AB=AC,AD=AE,AE的延长线与BC的延长线交于点F.求证: (1) ∠1=∠2 (2) AC  =AD
=AD  AF.
AF.
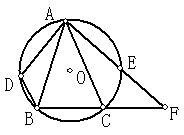
32.如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE·PO。①求证:PC是⊙O的切线;②若OE∶EA=1∶2,PA=16,求⊙O的半径;③在②的条件下,求sin∠PCA的值。

 33.已知:如图,△ABC是等腰直角三角形,且AD⊥BC,过AD的圆分别交AC、BC、AB于点E、F、G。①求证:GF=AE;②若AB=6,⊙O的半径为 33.已知:如图,△ABC是等腰直角三角形,且AD⊥BC,过AD的圆分别交AC、BC、AB于点E、F、G。①求证:GF=AE;②若AB=6,⊙O的半径为  ,求tan∠ADG的值。
,求tan∠ADG的值。
|