设本页为首页　　　　　　　　　　　　　　 　 　　　　　　　　　　　　　加入收藏
中文域名: 古今中外.com　　　　　　 英文域名：www.1-123.com　　　　　丰富实用的教育教学资料

[组图]初中毕业和高中阶段各类学校招生考试 查询数中考复习的详细结果 初中毕业和高中阶段各类学校招生考试 数 学 试 题 （满分：150分； 考试时间：120分钟） 考生须知： 1. 解答的内容一律写在答题卡上，否则以0分计算. 交卷时只交答题卡，本卷由考场处理，考生不得擅自带走. 2. 作图或画辅助线要用0.5毫米的黑色签字笔画好. 一、选择题（本大题共7小题，每小题3分，共21分）每小题都有四个选项，其中有且只有一个选项是正确的. 1. 下列计算正确的是 A. －1＋1＝0 B. －1－1＝0 C. 3÷ eq \f(1,3)＝1 D. 32＝6 2. 下列事件中是必然事件的是 A. 打开电视机，正在播广告. B. 从一个只装有白球的缸里摸出一个球，摸出的球是白球. C. 从一定高度落下的图钉，落地后钉尖朝上. D. 今年10月1日 ，厦门市的天气一定是晴天. 3. 如图1，在直角△ABC中，∠C＝90°,若AB＝5，AC＝4， 则sin∠B＝ A. eq \f(3,5) B. eq \f(4,5) C. eq \f(3,4) D. eq \f(4,3) 4. 下列关于作图的语句中正确的是 A. 画直线AB＝10厘米. B. 画射线OB＝10厘米. C. 已知A、B、C三点，过这三点画一条直线. D. 过直线AB外一点画一条直线和直线AB平行. 5. “比a的 eq \f(3,2)大1的数”用代数式表示是 A. eq \f(3,2)a＋1 B. eq \f(2,3)a＋1 C. eq \f(5,2)a D. eq \f(3,2)a－1 6. 已知：如图2，在△ABC中，∠ADE＝∠C，则下列等式成立的是 A. eq \f(AD,AB)＝ eq \f(AE,AC) B. eq \f(AE,BC)＝ eq \f(AD,BD) C. eq \f(DE,BC)＝ eq \f(AE,AB) D. eq \f(DE,BC)＝ eq \f(AD,AB) 7. 已知：a＋b＝m，ab＝－4, 化简（a－2）（b－2）的结果是 A. 6 B. 2 m－8 C. 2 m D. －2 m 二、填空题（本大题共10小题，每小题4分，共40分） 8. －3的相反数是 . 9. 分解因式：5x＋5y＝ . 10. 如图3，已知：DE∥BC，∠ABC＝50°,则∠ADE＝ 度. 11. 25÷23＝ . 12. 某班有49位学生，其中有23位女生. 在一次活动中，班上每一位学生的名字都各自写在一张小纸条上，放入一盒中搅匀. 假如老师闭上眼睛从盒中随机抽出一张纸条，那么抽到写有女生名字纸条的概率是 . 13. 如图4，⊙O的直径AB垂直于弦CD，垂足为E， 若∠COD＝120°，OE＝3厘米，则OD＝ 厘米. 14. 假如甲邀请乙玩一个同时抛掷两枚硬币的游戏，游戏的规 则如下：同时抛出两个正面，乙得1分；抛出其他结果， 甲得1分. 谁先累积到10分，谁就获胜.你认为 （填“甲”或“乙”）获胜的可能性更大. 15. 一根蜡烛在凸透镜下成一实像，物距u，像距v和凸透镜的焦距f 满足关系式： eq \f(1,u)＋ eq \f(1,v)＝ eq \f(1,f ). 若f＝6厘米，v＝8厘米，则物距u＝ 厘米. 16. 已知函数y＝ eq \r(－3x－1)－2 eq \r(2) ，则x的取值范围是 . 若x是整数，则此函数的最小值是 . 17. 已知平面直角坐标系上的三个点O（0，0）、A（－1，1）、B（－1，0），将△ABO绕点O按顺时针方向旋转135°,则点A、B的对应点A1、B1的坐标分别是A1（ ， ） ，B1( ， ) . 三、解答题（本大题共9小题，共89分） 18. (本题满分7分) 计算： 22＋(4－7)÷ eq \f(3,2)＋( eq \r(3)) EQ \S(0) 19. (本题满分7分) 一个物体的正视图、俯视图如图5所示， 请你画出该物体的左视图并说出该物体外形的名称. 20. (本题满分8分) 某市举行一次少年滑冰比赛，各年龄组的参赛人数如下表所示： 年龄组 13岁 14岁 15岁 16岁 参赛人数 5 19 12 14 (1) 求全体参赛选手年龄的众数、中位数； （2） 小明说，他所在年龄组的参赛人数占全体参赛人数的28%. 你认为小明是哪个年龄组的选手?请说明理由. 21. (本题满分10分) 如图6，已知：在直角△ABC中，∠C＝90°， BD平分∠ABC且交AC于D. （1）若∠BAC＝30°，求证: AD＝BD； （2）若AP平分∠BAC且交BD于P，求∠BPA的度数. 22. (本题满分10分) 某软件公司开发出一种图书治理软件，前期投入的开发、广告宣传费用共50000元，且每售出一套软件，软件公司还需支付安装调试费用200元. （1）试写出总费用y(元)与销售套数x(套)之间的函数关系式； （2）假如每套定价700元，软件公司至少要售出多少套软件才能确保不亏本？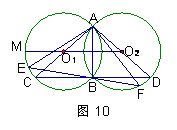 23. (本题满分10分) 已知：如图7，P是正方形ABCD 内一点，在正方形ABCD外有一点E， 满足∠ABE＝∠CBP，BE＝BP， (1) 求证：△CPB≌△AEB； (2) 求证：PB⊥BE； (3) 若PA∶PB＝1∶2，∠APB＝135°, 求cos∠PAE的值. 24. (本题满分12分) 已知抛物线y＝x2－2x＋m与x轴交于点A（x1，0）、B（x2，0）（x2＞x1）， (1) 若点P（－1，2）在抛物线y＝x2－2x＋m上，求m的值； （2）若抛物线y＝ax2＋bx＋m与抛物线y＝x2－2x＋m关于y轴对称，点Q1（－2，q1）、Q2（－3，q2）都在抛物线y＝ax2＋bx＋m上，则q1、q2的大小关系是 （请将结论写在横线上，不要写解答过程）； （友情提示：结论要填在答题卡相应的位置上） （3）设抛物线y＝x2－2x＋m的顶点为M，若△AMB是直角三角形，求m的值. 25. (本题满分12分) 已知：⊙O1与⊙O2相交于点A、B，过点B作CD⊥AB，分别交⊙O1和⊙O2于点C、D. （1）如图8，求证：AC是⊙O1的直径； （2）若AC＝AD， ① 如图9，连结BO2、O1 O2，求证：四边形O1C BO2是平行四边形； ② 若点O1在⊙O2外，延长O2O1交⊙O1于点M，在劣弧 eq \o(\s\up8(︵),\s\do0(MB))︵MB上任取一点E（点E与点B不重合）. EB的延长线交优弧 eq \o(\s\up8(︵),\s\do0(BDA))︵BDA于点F，如图10所示. 连结 AE、AF. 则AE AB（请在横线上填上 “≥、≤、＜、＞”这四个不等号中的一个）并加以证实. （友情提示：结论要填在答题卡相应的位置上） 26. (本题满分13分) 已知：O是坐标原点，P（m，n）(m＞0)是函数y ＝ eq \f(k,x) (k＞0)上的点，过点P作直线PA⊥OP于P，直线PA与x轴的正半轴交于点A（a，0）(a＞m). 设△OPA的面积为s，且s＝1＋eq \f(n4,4). （1）当n＝1时，求点A的坐标； （2）若OP＝AP，求k的值； (3 ) 设n是小于20的整数，且k≠ eq \f(n4,2)，求OP2的最小值. 厦门市2005年初中毕业和高中阶段各类学校招生考试 数学评分标准及参考答案 一、选择题（本大题共7小题，每小题3分，共21分）
题号	1	2	3	4	5	6	7
选项	A	B	B	D	A	C	D

二、填空题（本大题共10小题，每小题4分，共40分）

8. 3；9. 5(x＋y)；10. 50度；11. 4；12. eq \f(23,49)； 13. 6厘米 14. 甲 ； 15. 24 厘米；

16. x≤－ eq \f(1,3) ，－ eq \r(2) ； 17. A1 ( eq \r(2)，0)， B1( eq \f( eq \r(2),2)， eq \f( eq \r(2),2)）

注：8~15题每空4分；16、17题每空2分.第11题写成22不扣分.

三、解答题（本大题共9小题，共89分）

18. (本题满分7分）

解：22＋（4－7）÷ eq \f(3,2)＋( eq \r(3)) EQ \S(0)

＝4－3× eq \f(2,3)＋1 …… 4分

＝4－2＋1 …… 5分

＝3 …… 7分

注：每步运算1分.

19. (本题满分7分)

解： 左视图： …… 3分

该物体外形是： 圆柱 . …… 7分

20. （本题满分8分）

(1) 解： 众数是：14岁； 中位数是：15岁. …… 4分

(2) 解1：∵ 全体参赛选手的人数为：5＋19＋12＋14＝50名 …… 5分

又∵ 50×28% …… 6分

＝14（名） …… 7分

∴ 小明是16岁年龄组的选手. …… 8分

解2：∵全体参赛选手的人数为：5＋19＋12＋14＝50名 …… 5分

又∵16岁年龄组的选手有14名，

而14÷50 …… 6分

＝28% …… 7分

∴ 小明是16岁年龄组的选手. …… 8分

注：第（1）小题的众数、中位数各2分.

21. （本题满分10分）

(1) 证实：∵∠BAC＝30°∠C＝90°

∴ ∠ABC＝60° …… 1分

又∵ BD平分∠ABC ∴∠ABD＝30° …… 2分

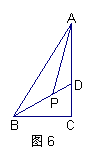∴ ∠BAC ＝∠ABD …… 3分

∴ BD＝AD …… 4分

(2) 解1： ∵∠C＝90°∴∠BAC＋∠ABC＝90° …… 5分

∴ eq \f(1,2)(∠BAC＋∠ABC)＝45° …… 6分

∵ BD平分∠ABC，AP平分∠BAC

∠BAP＝ eq \f(1,2)∠BAC ∠ABP＝ eq \f(1,2)∠ABC …… 8分

即∠BAP＋∠ABP＝45° …… 9分

∴∠APB＝180°－45°＝135° …… 10分

解2：∵∠C＝90° ∴∠BAC＋∠ABC＝90° …… 5分

∴ eq \f(1,2)(∠BAC＋∠ABC)＝45° …… 6分

∵ BD平分∠ABC，AP平分∠BAC

∠DBC＝ eq \f(1,2)∠ABC ∠PAC＝ eq \f(1,2)∠BAC …… 8分

∴ ∠DBC＋∠PAD＝45° …… 9分

∴ ∠APB＝∠PDA＋∠PAD ＝∠DBC＋∠C＋∠PAD

＝∠DBC＋∠PAD＋∠C ＝45°＋90°＝135° …… 10分

22. （本题满分10分）

(1) 解：y＝50000＋200x …… 4分

(2) 解1：设软件公司至少要售出x套软件才能确保不亏本，则有：

700 x≥50000＋200x …… 7分

解得：x≥100 …… 9分

答：软件公司至少要售出100套软件才能确保不亏本. …… 10分

解2：每套成本是 eq \f(50000,x)＋200 …… 5分

若每套成本和销售价相等则：700＝ eq \f(50000,x)＋200 …… 7分

解得：1＝ eq \f(100,x) ∴ x＝100 …… 9分

答：软件公司至少要售100套软件才能确保不亏本. …… 10分

解3：每套成本是 eq \f(50000,x)＋200 …… 5分

由题意得：700≥ eq \f(50000,x)＋200 …… 7分

解得：1≥ eq \f(100,x) ∴ x≥100 …… 9分

答：软件公司至少要售100套软件才能确保不亏本. …… 10分

注：第（1）小题的解析式可以不写x的取值范围.

23. （本题满分10分）

(1) 证实：∵ 四边形ABCD是正方形

∴ BC＝AB …… 1分

∵ ∠CBP＝∠ABE BP＝BE …… 2分

∴ △CBP≌△ABE …… 3分

(2) 证实：∵∠CBP＝∠ABE

∴∠PBE＝∠ABE ＋∠ABP …… 4分

＝∠CBP＋∠ABP

＝90° …… 5分

∴ PB⊥BE …… 6分

（1）、（2）两小题可以一起证实.

证实：∵∠CBP＝∠ABE

∴∠PBE＝∠ABE ＋∠ABP …… 1分

＝∠CBP＋∠ABP

＝90° …… 2分

∴ PB⊥BE …… 3分

以B为旋转中心，把△CBP按顺时针方向旋转90°， …… 4分

∵ BC＝AB ∠CBA＝∠PBE＝90° BE＝BP …… 5分

∴△CBP与△ABE重合

∴ △CBP≌△ABE …… 6分

(3) 解：连结PE

∵ BE＝BP ∠PBE＝90°

∴∠BPE＝45° …… 7分

设 AP为k，

则 BP＝BE＝2k

∴ PE2＝8k2 …… 8分

∴ PE＝2 eq \r(2)k

∵∠BPA＝135° ∠BPE＝45°

∴∠APE＝90° …… 9分

∴AE＝3 k

在直角△APE中： cos∠PAE＝ eq \f(AP,AE)＝ eq \f(1,3) …… 10分

24. （本题满分12分）

(1) 解：∵点P（－1，2）在抛物线y＝x2－2x＋m上 …… 1分

∴ 2＝(－1) EQ \S(2) －2×(－1)＋m …… 2分

∴ m＝－1 …… 3分

(2) 解： q1＜q2 …… 7分

(3) 解1：∵ y＝x2－2x＋m

＝(x－1) EQ \S(2) ＋m－1

∴ M (1，m－1) …… 8分

∵ 抛物线 y＝x2－2x＋m开口向上，

且与x轴交于点A（x1，0）、B（x2，0）（x1＜x2）

∴ m－1＜0

∵ △AMB是直角三角形，又AM＝MB

∴∠AMB＝90° △AMB是等腰直角三角形 …… 9分

过M作MN⊥x轴，垂足为N. 则N（1，0）

又 NM＝NA

∴ 1－x1＝1－m

∴ x1＝m …… 10分

∴ A (m，0)

∴ m2－2 m＋m＝0 ∴m＝0 或m＝1（不合题意，舍去） …… 12分

解2：又 NM＝NA＝NB

∴ x2－x1＝2－2m

∴ eq \b\lc\{( eq \a\al\co1\vs8(x2＋x1＝2,x2－x1＝2－2m)) 解得： eq \b\lc\{( eq \a\al\co1\vs8(x1＝m,x2＝2－m)) …… 10分

∴ A (m，0)

∴ m2－2 m＋m＝0

∴ m＝0 或m＝1（不合题意，舍去） …… 12分

25. （本题满分12分）

(1) 证实：∵ CD⊥AB …… 1分

∴∠ABC＝90° …… 2分

∴ AC是⊙O1的直径 …… 3分

(2)

① 证实1：∵ CD⊥AB ∴∠ABD＝90°

∴ AD是⊙O2的直径 …… 4分

∵ AC＝AD

∵ CD⊥AB ∴CB＝BD …… 5分

∵ O1、O2分别是AC、AD的中点

∴ O1O2∥CD且 O1O2＝ eq \f(1,2)CD＝CB …… 6分

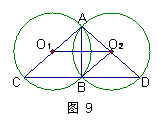∴ 四边形O1C BO2是平行四边形 …… 7分

证实2：∵ CD⊥AB ∴∠ABD＝90°

∴ AD是⊙O2的直径 …… 4分

∵ AC＝AD

∵ CD⊥AB ∴CB＝BD …… 5分

∵ B、O2分别是CD、AD的中点

∴ BO2∥AC且 BO2＝ eq \f(1,2)AC＝O1C …… 6分

∴ 四边形O1C BO2是平行四边形 …… 7分

证实3：∵ CD⊥AB ∴∠ABD＝90°

∴ AD是⊙O2的直径 …… 4分

∵ O1、O2分别是AC、AD的中点

∴ O1O2∥CD …… 5分

∵ CD⊥AB ∴ CB＝BD

∴ B是CD的中点

∴O2B∥O1C …… 6分

∴四边形O1C BO2是平行四边形 …… 7分

证实4：∵ CD⊥AB ∴∠ABD＝90°

∴ AD是⊙O2的直径 …… 4分

∵ AC＝AD

∴ O1C＝O2B

∴ ∠C＝∠D ------------------------------------------------ 5分

∵ O2B＝O2D

∴∠O2B D＝∠D ……∴∠C＝∠O2B D

∴O2B∥O1C …… 6分

∴四边形O1C BO2是平行四边形 …… 7分

② AE ＞ AB …… 8分

证实1：当点E在劣弧 eq \o(\s\up8(︵),\s\do0(MC))︵MC上(不与点C重合)时，

∵ AC＝AD

∴ ∠ACD＝∠ADC

∴ ∠AEB＝∠ACD＝∠ADC＝∠AFB

∴ AE＝AF …… 9分

记AF交BD为G ∵ AB⊥CD

∴ AF＞AG＞AB …… 10分

当点E与点C重合时，AE＝AC＞AB

当点E在劣弧 eq \o(\s\up8(︵),\s\do0(CB))︵CB上 (不与点B重合) 时，设AE交CD与H，

AE＞AH＞AB …… 11分

综上，AE＞AB. …… 12分

证实2：当点E在劣弧 eq \o(\s\up8(︵),\s\do0(MC))︵MC上(不与点C重合)时，

连结EC、DF ，∵ AD是⊙O2的直径，即∠AFD＝90°

∠EAC＝∠EBC＝∠DBF＝∠DAF

∵ AC＝AD 直角△AFD≌直角△AEC

∴ AE＝AF …… 9分

证实3：当点E在劣弧 eq \o(\s\up8(︵),\s\do0(MC))︵MC上(不与点C重合)时，

连结EC、DF ，∵ AD是⊙O2的直径，即∠AFD＝90°

∵ ∠DBF＝∠DAF ∴∠ADF＋∠DBF＝90°

又∵ ∠DBF＝∠EBC ∠ABE＋∠EBC＝90°

∴ ∠ADF＝∠ABE

∵ ∠ABE＝∠ACE ∴∠ADF＝∠ACE

∵ AC＝AD ∴ 直角△AFD≌直角△AEC

∴ AE＝AF …… 9分

26. （本题满分13分）

解：过点P作PQ⊥x轴于Q，则PQ＝n，OQ＝m

(1) 当n＝1时， s＝ eq \f(5,4) …… 1分

∴ a＝ eq \f(2s,n)＝ eq \f(5,2) …… 3分

(2) 解1： ∵ OP＝AP PA⊥OP

∴△OPA是等腰直角三角形 …… 4分

∴ m＝n＝ eq \f(a,2) …… 5分

∴ 1＋ eq \f(n4,4)＝ eq \f(1,2)·an

即n4－4n2＋4＝0 …… 6分

∴ k2－4k＋4＝0

∴ k＝2 …… 7分

解2：∵ OP＝AP PA⊥OP

∴△OPA是等腰直角三角形 …… 4分

∴ m＝n …… 5分

设△OPQ的面积为s1

则：s1＝ eq \f(s,2)

∴ eq \f(1,2)·mn＝ eq \f(1,2)(1＋ eq \f(n4,4))

即：n4－4n2＋4＝0 …… 6分

∴ k2－4k＋4＝0

∴ k＝2 …… 7分

(3) 解1：∵ PA⊥OP， PQ⊥OA

∴ △OPQ∽△OAP

设：△OPQ的面积为s1，则

eq \f(s1,s)＝ eq \f(PO2,AO2) …… 8分

即： eq \f( eq \f(1,2)k,1＋eq \f(n4,4)) ＝ eq \f(n2＋ eq \f(k2,n2), eq \f(4 (1＋ eq \f(n4,4)) EQ \S(2) , n2))

化简得：2n4＋2k2－k n4－4k＝0 …… 9分

（k－2）（2k－n4）＝0

∴k＝2或k＝ eq \f(n4,2)(舍去) …… 10分

∴当n是小于20的整数时，k＝2.

∵ OP2＝n2＋m2＝n2＋ eq \f(k2,n2)

又m＞0，k＝2，

∴ n是大于0且小于20的整数

当n＝1时，OP2＝5

当n＝2时，OP2＝5

当n＝3时，OP2＝32＋ eq \f(4,32)＝9＋ eq \f(4,9)＝ eq \f(85,9) …… 11分

当n是大于3且小于20的整数时，

即当n＝4、5、6、…、19时，OP2得值分别是：

42＋ eq \f(4,42)、52＋ eq \f(4,52)、62＋ eq \f(4,62)、…、192＋ eq \f(4,192)

∵192＋ eq \f(4,192)＞182＋ eq \f(4,182)＞…＞32＋ eq \f(4,32)＞5 …… 12分

∴ OP2的最小值是5. …… 13分

解2： ∵ OP2＝n2＋m2＝n2＋ eq \f(k2,n2)

＝n2＋ eq \f(22,n2)

＝(n－ eq \f(2,n)) EQ \S(2) ＋4 …… 11分

当n＝ eq \f(2,n) 时，即当n＝ eq \r(2)时，OP2最小；

又∵n是整数，而当n＝1时，OP2＝5；n＝2时，OP2＝5 …… 12分

∴ OP2的最小值是5. …… 13分

解3：∵ PA⊥OP， PQ⊥OA

∴ △OPQ∽△P AQ

eq \f(PQ,QA)＝ eq \f(OQ,PQ) …… 8分

eq \f(n,a－m)＝ eq \f(m,n)

化简得：2n4＋2k2－k n4－4k＝0 …… 9分

（k－2）（2k－n4）＝0

∴k＝2或k＝ eq \f(n4,2)(舍去) …… 10分

解4：∵ PA⊥OP， PQ⊥OA

∴ △OPQ∽△P AQ

eq \f(s1,s－s1)＝ eq \f(OQ2,PQ2) …… 8分

化简得：2n4＋2k2－k n4－4k＝0 …… 9分

（k－2）（2k－n4）＝0

∴k＝2或k＝ eq \f(n4,2)(舍去) …… 10分

解5：∵ PA⊥OP， PQ⊥OA

∴ △OPQ∽△OAP

∴ eq \f(OP,OA)＝ eq \f(OQ,OP) …… 8分

∴ OP2＝OQ·OA

化简得：2n4＋2k2－k n4－4k＝0 …… 9分

（k－2）（2k－n4）＝0

∴k＝2或k＝ eq \f(n4,2)(舍去) …… 10分