中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
一、选择题：（本大题共10题，每小题3分，共30分） 每小题给出四个答案，其中只有一个符合题目的要求，请把选出的答案编号填在下面的答题表一内，否则不给分. 答题表一
| 题号
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 答案
|
|
|
|
|
|
|
|
|
| | |||||||||||||||||||||||||||||||||||
1、在0，-1，1，2这四个数中，最小的数是
A、-1 B、0 C、1 D、2
2、我们从不同的方向观察同一物体时，可以看到不同的平面图形，如图，从图的左面看这个几何体的左视图是
 | |||||||||
 |
 | ||||||||
 | |||||||||
 | |||||||||
A B C D
3、方程x2 = 2x的解是
A、x=2 B、x1= 
4、长城总长约为6700010米，用科学记数法表示是（保留两个有效数字）
A、6.7×105米 B、6.7×106米 C、6.7×107米 D、6.7×108米
5、函数y= 
A、第一、三象限 B、第三、四象限 C、A、第一、二象限 D、第二、四象限
6、图所列图形中是中心对称图形的为
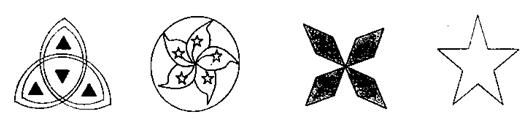
A B C D
7、中心电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标中，有5个商标牌的背面注明了一定的奖金额，其余商标的背面是一张苦脸，若翻到它就不得奖。参加这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均得若干奖金，假如翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率是
A、 
8、实数a、b在数轴上的位置如图所示，那么化简|a-b|- 
|
b |
|
O |
|
a |
 |
A、2a-b B、b C、-b D、-2a b
9、一件衣服标价132元，若以9折降价出售，仍可获利10%，则这件衣服的进价是
A、106元 B、105元 C、118元 D、108元
10、如图，AB是⊙O的直径，点D、E是半圆的三等分点，AE、BD的延长线交于点C，若CE=2，则图中阴影部分的面积是
A、 
二、填空题：（本大题共5小题，每小题3分，共15分，请将答案填入答题表二内，否则不给分）
答题表二
题号
11
12
13
14
15
答案
11、一组数据3、8、8、19、19、19、19的众数是__。
|
温度℃ |
|
温度℃ |
|
（1）2004年6月上旬 |
|
（2）2005年6月上旬 |
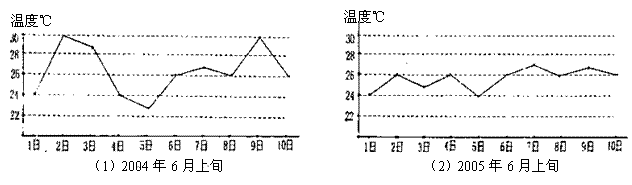12、图（1）（2）是根据某地近两年6月上旬日平均气温情况绘制的折线统计图，通过观察图表，可以判定这两年6月上旬气温比较稳定的年份是__。
13、如图，已知，在△ABC和△DCB中，AC=DB，若不增加任何字母与辅助线，要使△ABC≌△DCB，则还需增加一个条件是__。
|
D |
|
A |
|
B |
|
C |
|
E |
|
F |
|
14、已知： 
|
D |
|
B |
|
C |
 |
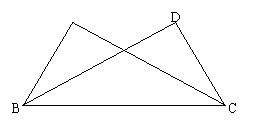（13） （15）
15、如图，口ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的点F，若△FDE的周长为8，△FCB的周长为22，则FC的长为__。
三、解答题：（共7题，共55分）
16、（6分）计算：( 
17、（6分）先化简，再求值：（ 
|
D |
|
A |
|
C |
|
B |
18、（8分）大楼AD的高为10米，远处有一塔BC，某人在楼底A处测得踏顶B处的仰角为60º，爬到楼顶D点测得塔顶B点的仰角为30º，求塔BC的高度。
19、（8分）右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
（1）求该班有多少名学生？
（2）补上步行分布直方图的空缺部分；
（3）在扇形统计图中，求骑车人数所占的圆心角度数。
（4）若全年级有500人，估计该年级步行人数。
|
20 |
|
12 |
|
8 |
|
乘车 |
|
步行 |
|
骑车 |
|
步行50% |
|
步行 20% |
|
骑车 30% |
 | |||
| |||
20、某工程，甲工程队单独做40天完成，若乙工程队单独做30天后，甲、乙两工程队再合作20天完成。
（1）（5分）求乙工程队单独做需要多少天完成？
（2）（4分）将工程分两部分，甲做其中一部分用了x天，乙做另一部分用了y天，其中x、y均为正整数，且x<15，y<70，求x、y.
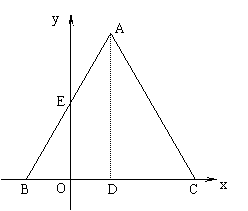
21、已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与y轴的正半轴相交于点E，点B（-1，0），P是AC上的一个动点（P与点A、C不重合）
（1）（2分）求点A、E的坐标；
（2）（2分）若y= 
（3）（5分）连结PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L的最小值，并判定此时点P是否在（2）中所求的抛物线上，请充分说明你的判定理由。
|
A |
|
B |
|
C |
|
O |
|
D |
|
E |
|
y |
|
x |
 |
22、（9分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合。
|
A |
|
O |
|
D |
|
B |
|
H |
|
E |
|
C |
（1）（5分）求证：△AHD∽△CBD
（2）（4分）连HB，若CD=AB=2，求HD HO的值。
参考答案
一、选择题：
ABCBD CBCDA
二、填空题：
11、19 12、2005年 13、AB=DC 14、19 15、7
三、解答题：
16、解: 原式=1 3-5-1= -2
17、解：原式= 
|
D |
|
A |
|
C |
|
B |
|
E |
 |
18、解：作BE⊥AD的延长线于点E
设ED= x
在Rt△BDE中，BE= 
在Rt△ABE中，AE=
由AE-ED=AD
得：3x-x=10 解之得：x=5
所以BC=5 10=15
|
20 |
|
12 |
|
8 |
|
乘车 |
|
步行 |
|
骑车 |
答：塔BC的高度为15米。
|
步行50% |
|
步行 20% |
|
骑车 30% |
19、解：（1）40人
（2）见直方图
（3）圆心角度数= 
（4）估计该年级步行人数=500×20%=100
20、解：（1）设乙工程队单独做需要x天完成。
则30× 
经检验得x=100是所列方程的解，所以求乙工程队单独做需要100天完成。
（2）甲做其中一部分用了x天，乙做另一部分用了y天
所以 
所以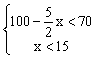 
又y也为正整数，所以x=14，y=65
21、
|
A |
|
B |
|
C |
|
O |
|
D |
|
E |
|
y |
|
x |
解：（1）连结AD，不难求得A（1，2
OE= 
（2）因为抛物线y=
由待定系数法得：c= 
抛物线的解析式为y= 
（3）大家记得这样一个常识吗？
“牵牛从点A出发，到河边l喝水，再到点B处吃草，走哪条路径最短？”即确定l上的点P
方法是作点A关于l的对称点A'，连结A'B与l的交点P即为所求.
|
A |
|
B |
|
l |
 |
本题中的AC就是“河”，B、D分别为“出发点”和“草地”。
|
A |
|
B |
|
C |
|
O |
|
D |
|
E |
|
y |
|
x |
|
P |
|
D' |
|
F |
|
G |
由引例并证实后，得先作点D关于AC的对称点D'，
连结BD'交AC于点P，则PB与PD的和取最小值，
即△PBD的周长L取最小值。
不难求得∠D'DC=30º
DF=
求得点D'的坐标为（4，
直线BD'的解析式为： 
直线AC的解析式为： 
求直线BD'与AC的交点可得点P的坐标（ 
此时BD'= 
所以△PBD的最小周长L为2
把点P的坐标代入y=
22、
|
A |
|
O |
|
D |
|
B |
|
H |
|
E |
|
C |
（1）证实：略
（2）设OD=x，则BD=1-x，AD=1 x
证Rt△AHD∽Rt△CBD
则HD : BD=AD : CD
即HD : (1-x)=(1 x) : 2
即HD= 
在Rt△HOD中，由勾股定理得：
OH= 
所以HD HO=
注重：当点E移动到使D与O重合的位置时，这时HD与HO重合，由Rt△AHO∽Rt△CBO，利用对应边的比例式为方程，可以算出HD=HO= 
| |
