|
与圆有关的基本概念
(时间:100分钟 总分:100分)
一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.在同圆或等圆中,假如 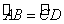 ,则AB和CD的关系( )
,则AB和CD的关系( )
A.AB=CD B.AB>CD C.AB<CD D.AB=2CD
2.已知⊙O1和⊙O2的半径分别为3cm和5cm,两圆的圆心距是6cm,则两圆的位置关系是( )
A.内含 B.外离 C.内切 D.相交
3.下列命题中,不正确的是( )
A.圆是轴对称图形; B.圆是中心对称图形
C.过三点一定确定一个圆; D.一个三角形只有一个外接圆
4.到△ABC的三个顶点距离相等的点是△ABC的( )
A.三条中线的交点; B.三条角平分线的交点
C.三条高的交点; D.三条边的垂直平分线的交点
5.下列命题中是假命题的是( )
A.直径是弦; B.等弧所在的圆是同圆或等圆
C.弦的垂直平分线经过圆心; D.平分弦的直径垂直于弦
6.若圆的半径是5cm,圆心的坐标是(0,0),点P的坐标是(4,2),则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内
C.点P在⊙O上 D.点P在⊙O外或⊙O上
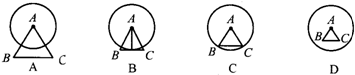
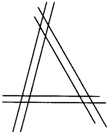
7.已知等边△ABC的边长为2 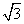 cm,如图所示,以A为圆心的各圆中,半径是3cm的圆是( )
cm,如图所示,以A为圆心的各圆中,半径是3cm的圆是( )
8.一个点与圆上最近点的距离是4cm,最远点的距离是为9cm,则此圆的半径为( )
A.2.5cm或6.5cm B.2.5cm C.6.5cm D.13cm或5cm
9.已知⊙O1和⊙O2的半径分别为R、r,O1O2=d,且R2-r2 d2=2Rd,则两圆的位置关系是( )
A.内含 B.内切 C.相交 D.相切
10.如图1,已知直线L和直线L外两定点A、B,且A、B到直线L的距离相等,则经过A、B两点且圆心在L上的圆有( )
A.0个 B.1个 C.无数个 D.0个或1个或无数个
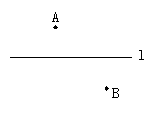  
(1) (2) (3)
二、填空题(本大题共8小题,每小题3分,共24分)
11.半径为2,圆心角为120°的扇形的面积为_________.
12.已知⊙O1和⊙O2外切,且圆心距为10cm,若⊙O1的半径为3cm,⊙O2的半径为_____.
13.圆的半径为3,则弦长x的取值范围是________.
14.如图2,圆周角∠ACB=34°,则圆心角∠AOB的度数为________.
15.已知一弧的半径为3,弧长为2 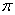 ,则此弧所对的圆心角为________.
,则此弧所对的圆心角为________.
16.若一个圆锥的母线长是5cm,底面半径是3cm,则它的侧面展开图的面积是_______.
17.已知⊙O的半径为6.5cm,点P为直线L上一点,且OP=6.5cm,则直线与⊙O的位置关系是________.
18.已知⊙O1、⊙O2的半径都等于1,有下列命题:①若O1O2=1,则⊙O1和⊙O2有两个公共点;②若O1O2=2,则⊙O1与⊙O2外切;③若O1O2≤3,则⊙O1和⊙O2必有公共点.其中正确的命题的序号是_________.
三、解答题(本大题共46分,19~23题每题6分,24题、25题每题8分,解答题应写出文字说明、证实过程或演算步骤)
19.求证:直径是圆中最长的弦.
20.某市为筹办一个大型运动会,该市政府打算修建一个大型体育中心,在选址过程中,有人建议该体育中心所在位置到该市三条主要公路的距离相等,若采纳此人建议,请你在图3中作出体育中心的位置(不写作法,只保留作图痕迹).
21.已知直线L:y=x-2,点A(0,-2),点B(2,0),设点P为L上一点,试判定过P、A、B三点能否作一个圆.
22.如图,在△ABC中,∠A=30°,AC=8,BC=5,以直线AB为轴将△ABC旋转一周得到一个旋转体,求这个旋转体的表面积.

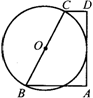
23.已知:如图,梯形ABCD中,AB∥CD,∠A=90°,BC=AB CD,BC是⊙O的直径,求证:⊙O与AD相切.
24.相交两圆的公共弦为6,两圆的半径分别为3 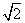 和5,则这两圆的圆心距为多少?
和5,则这两圆的圆心距为多少?
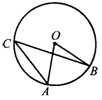
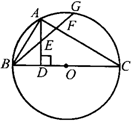
25.如图,BC为⊙O的直径,G是半圆上任一点,点A为 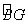 的中点,AD⊥BC,求证:
的中点,AD⊥BC,求证:
(1)BE=AE;(2)AB是BE、BG的比例中项.
答案:
一、选择题
1.A 2.D 3.C 4.D 5.D 6.B 7.B 8.A 9.D 10.B
二、填空题
11. 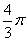 12.7cm 13.0<x≤6 14.68° 15.120°
12.7cm 13.0<x≤6 14.68° 15.120°
16.15 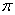 cm2 17.相交或相切 18.①②
cm2 17.相交或相切 18.①②
三、解答题
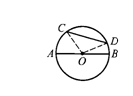 19.解:已知:如图,在⊙O中,AB是直径,CD是任意的一条非直径弦. 19.解:已知:如图,在⊙O中,AB是直径,CD是任意的一条非直径弦.
求证:AB>CD.
证实:连结OC、OD,则AB=OA OB=OC OD.
在△OCD中,OC OD>CD,所以AB>CD.
20.解:有四种情况(图略).
21.解:点A(0,-2),点B(2,0)均在直线y=x-2上,而点P也为L上一点,故过P、A、B三点不能作一个圆.
22.解:过点C作CD⊥AB,则由∠A=30°,知CD=4,则旋转一周的周长为8 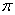 ,
,
设旋转体上半部分与下半部分的侧面展开图中的圆心角分别为θ1与θ2,
则 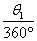 ·2
·2 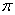 ·AC=8
·AC=8 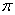 ,
, 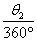 ·2
·2 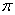 ·BC=8
·BC=8 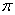 ,
,
∴θ1=180°,θ2=288°.
则全面积为 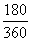 ·
· 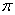 ·AC2
·AC2  ·
· 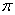 ·BC2=52
·BC2=52  .
.
23.证实:过点O作OE⊥AD于E,则:
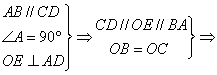 OE是梯形的中位线
OE是梯形的中位线
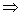 OE=
OE= 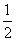 (BA CD)=
(BA CD)= 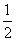 BC.
BC.
∴OE是半径,∴AD与⊙O相切.
24.解:当两圆的圆心在公共弦同侧时,圆心距为1,
当两圆的圆心在公共弦异侧圆心距为7.
25.证实:(1)BC是直径 ∠BAC=90°,
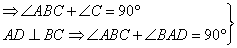
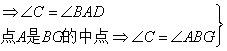
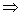 ∠BAD=∠ABG
∠BAD=∠ABG 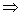 BE=AE.
BE=AE.
(2)连结CG,则在Rt△ABC中,AD⊥BC,
∴AB2=BD·BC.
又∵∠BDE=∠BGC=90°,∠GBC=∠GBC,
∴△GBC∽△DBE, 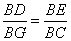 .
.
∴BD·BC=BE·BG. ∴AB2=BE·BG.
∴AB是BE、BG的比例中项.毛
|