一、填空题（每小题3分，共36分）
1. -2的倒数是 。
2. 分解因式： 
3. 一种商品每件成本100元，按成本增加20%定出价格，则每件商品的价格是 元。
4.
|
A |
|
O |
|
P |
|
B |
|
图（1） |
在方程 
5. 函数 
6. △ABC中，D、E分别是AB、AC的中点，若BC=6，则DE= 。
7.
|
A |
|
B |
|
C |
|
D |
|
P |
|
· |
|
O |
|
图（2） |
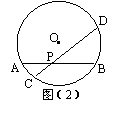如图（1），已知AB是⊙O的弦，OA=5，OP⊥AB，垂足为P，且OP=3，则AB= 。
8. 如图（2），弦AB和CD交于内一点P，若AP=3，PB= 4，CP=2，则PD= 。
9. 已知：⊙O1的半径为3，⊙O2的半径为4，若⊙O1与⊙O2相外切，则O1O2= 。
10. 将一批数据分成5组列出频率分布表，其中前4组的频率之和为0.9,则第5项的 频率为 .
11.
|
图（3） |
|
A1 |
|
A100 |
|
A9 |
|
A8 |
|
A6 |
|
A5 |
|
A4 |
|
A3 |
|
A2 |
|
A7 |
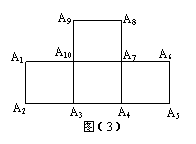圆锥的母线长为8,侧面展开图的圆心角为90°,则它的底面半径为 .
12. 如图（3），在四个正方形拼接成的图形中，以这十个点中任意三点为顶点，共能组成 个等腰直角三角形。你愿意把得到上述结论的探究方法与他人交流吗？若愿意，请在下方简要写出你的探究过程（结论正确且所写的过程灵敏合理可另加2分，但全卷总分不超过150分）
二．选择题（每小题4分，共24分）
|
A |
|
D |
|
C |
|
B |
|
· |
|
O |
|
图（4） |
13．下列计算正确的是（ ）
A．a3·a2 = a5 B. a3÷a=a 3
C. (a2)3 = a 5 D. (
14.一元二次方程x2－5x 2=0的两个根为x1 , x2 ，则x1 x2等于（ ）
A. –2 B.
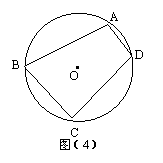
15.如图（4），在⊙O的内接四边形ABCD中，若∠BAD=110°，则∠BCD等于
( )
A．110° B.90° C.70° D.20°
16.用配方法将二次三项式a2
A.(a–2)2 1 B.(a 2)2 1
C.(a –2)2-1 D.(a 2)2-1
17.假如只用正三角形作平面镶嵌（要求镶嵌的正三角形的边与另一正三角形有边重合），则在它的每一个顶点四周的正三角形的个数为（ ）
A． 3 B.
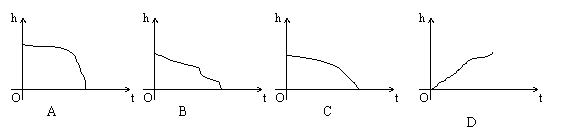
18.某爱好小组做实验，将一个装满水的啤酒瓶倒置（如图（5）），并设法使瓶里的水从瓶中匀速流出。那么该倒置啤酒瓶内水面高度h随水流出的时间t变化的图象大致是（ ）
|
O |
|
h |
|
t |
|
A |
|
O |
|
h |
|
t |
|
B |
|
O |
|
h |
|
t |
|
C |
|
O |
|
h |
|
t |
|
D |
 |
三．解答题（共90分）
19．（8分）计算：
解：
20．（8分）先化简下面的代数式，再求值：
解：
|
2 |
|
A |
|
C |
|
B |
|
D |
|
1 |
21．（8分）解不等式组：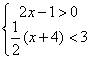 
解：
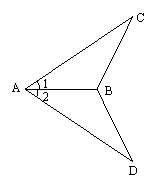
22．（8分）如图，已知：AC=AD，BC=BD
求证：∠1=∠2
证实：
|
93米 |
|
A |
|
B |
|
F |
|
E |
|
D |
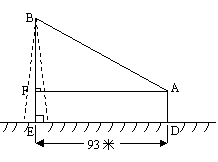23．（8分）如图，在离铁塔（1） 若∠BAF=31°，求铁塔高BE（精确到
（2） 若∠BAF=30°，求铁塔高BE（精确到
解：
24．（8分）在一次测验中，某学习小组的5名学生的成绩如下（单位：分）
68 75 67 66 99
（1） eq oac(○,1)1求这组成绩的平均分 
eq oac(○,2)2求去掉一个最高分后的其余4个成绩的平均分 
（3） 在题（1）所求得的
解：
25．（8分）如图，△ABC中，∠BAC的平分线AD交BC于D，⊙O过点A，且和BC切于D，和AB、AC分别交于E、F。设EF交AD于G ，连结DF。
（1）
|
· |
|
B |
|
D |
|
C |
|
F |
|
E |
|
A |
|
G |
|
O |
求证：EF∥BC ；
（2） 已知：DF =2 ，AG =3 ，求 
26．（8分）已知抛物线 
（1） 求b的值；
（2）
|
O |
|
x |
|
y |
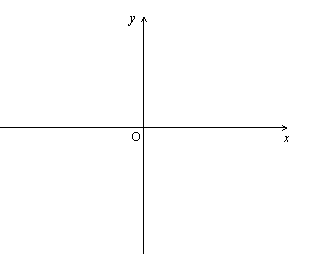设P为此抛物线的顶点，B（a ,0）（a≠1）为抛物线上的一点，Q是坐标平面内的点。假如以A、B、P、Q为顶点的四边形为平行四边形，试求线段PQ的长。
解：
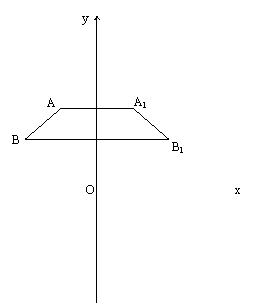
27．（13分）如图，在直角坐标系中，等腰梯形ABB
（1） 请画出：点A、B关于原点O的对称点A2 、B2（应保留画图痕迹，不必写画法，也不必证实）；
（2） 连结A
（3）
|
O |
|
x |
|
y |
|
A |
|
B |
|
A1 |
|
B1 |
设线段AB两端点的坐标分别为A（-2 ，4）、B（-4 ，2），连结（1）中A2B2 ，试问在χ轴上是否存在点C ，使△A1B解：
28．（13分）周末某班组织登山活动，同学们分甲、乙两组从山脚下沿着一条道路同时向山顶进发。设甲、乙两组行进同一段所用的时间之比为2∶3 。
（1） 直接写出甲、乙两组行进速度之比；
（2） 当甲组到达山顶时，乙组行进到山腰A处，且A处离山顶的路程尚有
（3） 在题（2）所述内容（除最后的问句外）的基础上，设乙组从A处继续登山，甲组到达山顶后休息片刻，再从原路下山，并且在山腰B处与乙组相遇。请你先根据以上情景提出一个相应的问题，再给予解答（要求： eq oac(○,1)1问题的提出不得再增添其他条件； eq oac(○,2)2问题的解决必须利用上述情景提供的所有已知条件）
参考答案：
一、填空：
1． 
二、选择题 ADCBDC
三、解答：
19．原式=3-1 4 20.原式=x2-2xy 2xy-2y2 当x=1,y=
=6 =x2-y2 原式=12-(
21.解：解不等式 eq oac(○,1)1，得x> 
|
2 |
在数轴上表示不等式 eq oac(○,1)1、 eq oac(○,2)2的解集：
22．证实：在△ABC和△ABD中
∴△ABC≌△ABD ∴∠1=∠2
23．解：（1）在Rt△ABF中，∵tan∠BAF = 
∴BE=BF FE=BF AD≈55。880 1.55=57.430≈57.43(米)
答：铁塔高BE约长为
（2）在Rt△ABF中，∵tan∠BAF = 
答：铁塔高BE约为
24．解：（1） eq oac(○,1)1 
将5个成绩从小到大的顺序排列为：66 67 68 75 99 ∴中位数M=68（分）
eq oac(○,2)2 
（3） M与
25.证实：∵⊙O切BC于D，∴∠4=∠2 又∵∠1=∠3，∠1=∠2
∴∠3=∠4 ∴EF∥BC
（2）解：∵∠1=∠3，∠1=∠2 ，∴∠2=∠3 又∵∠5=∠5，∴△ADF∽△FDG ∴ 
设GD=x ,则 
|
O |
|
Q |
|
P |
|
Q |
|
x |
|
A |
|
Q |
|
Y |
|
B |
26．解：（1）由题意得2×12 b×1-2=0 ∴b=0
(2)由（1）知y=2x2-2 ∴抛物线的顶点为（0，-2）
∵B（a,0）(a≠1)为抛物线上的点，∴
∴B(-1,0) 符合题意的Q点在坐标平面内的位置有下述三种：
如图， eq oac(○,1)1当Q在y轴上时, ∵四边形QBPA为平行四边形，可得QO=OP=2，∴PQ=4
eq oac(○,2)2当点Q在第四象限时，∵四边形QBPA为平行四边形，∴PQ=AB=2
eq oac(○,3)3当点Q在第三象限时，同理可得PQ=2。
27.解：（1）如图，A2、B2为所求的点
（2）（证法1）设A（x1,y1）、B(x2,y2) 依题意与（1）可得A1(-x1,y1),B1(-x2,y2), A2(-x1,-y1),B2(-x2,-y2)
∴A1、、B1关于x轴的对称点是A2、B2，∴x轴垂直平分线段A
（3）存在符合题意的C点。由（2）知A1与A2，B1与B2均关于x轴对称, ∴连结A2B1交x轴于C，点C为所求的点。 ∵A（-2，4），B（-4，2） 依题意及（1）得B1（4，2），A2（2，-4）
设直线A2B1的解析式为y=kx b 则有 
令y=0,得x= 
28．解：（！）甲、乙两组行进速度之比为3∶2
（2）（法1）设山脚离山顶的路程为S千米，依题意可列方程： 
（4） 可提问题：“问B处离山顶的路程小于多少千米？”再解答：设B处离山顶的路程为m千米（m>0）甲、乙两组速度分别为3k千米/时，2k千米/时（k>0）依题意得： 
答：B处离山顶的路程小于
